UAV-UGV Cooperation For Objects Transportation In An Industrial Area
- 1 Introduction
- 1.1 Motivation and related works
- 1.2 Contribution and orgnization
- 2 Problem Statement
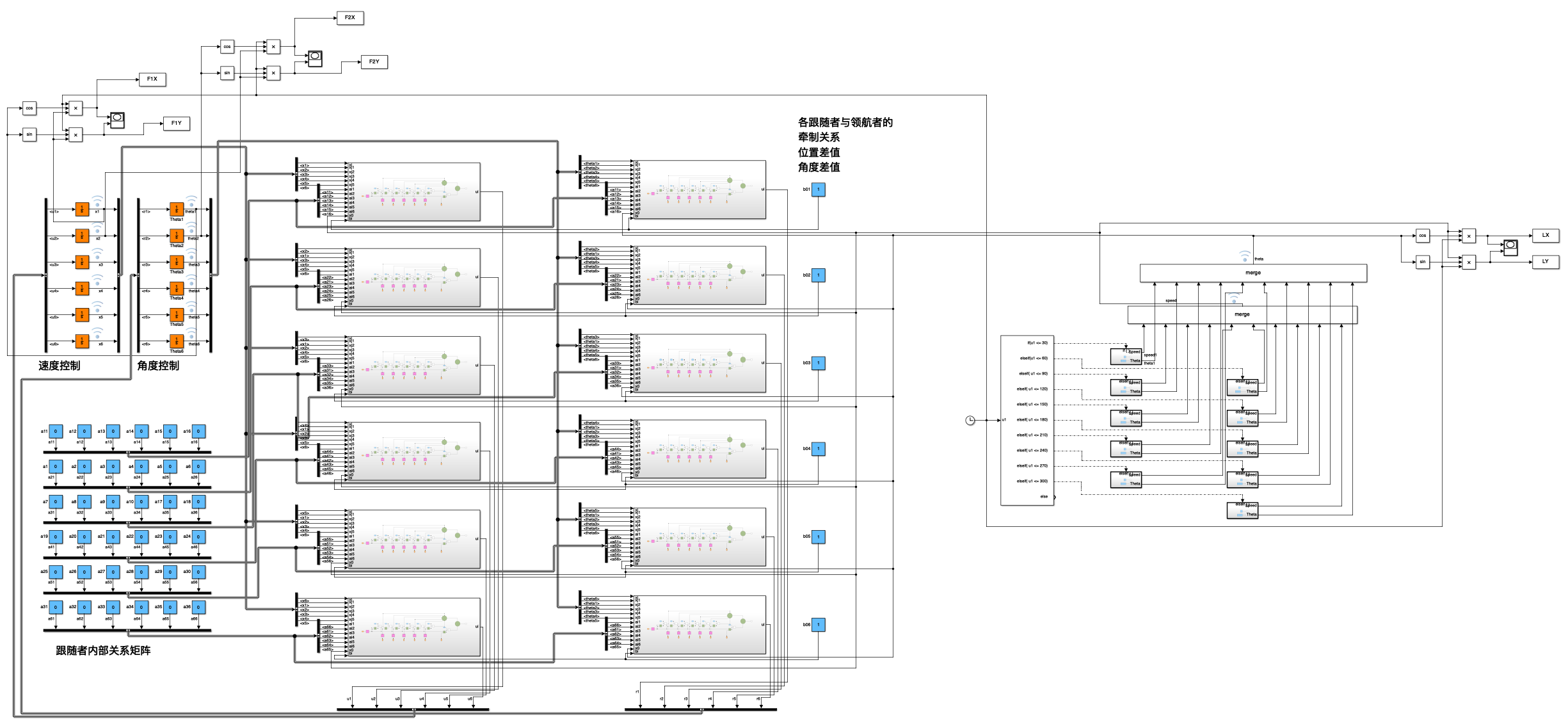
- 3 Architecture configuration
- 3.1 Hardware configuration
- 3.2 Overall architecture
- 3.3 First layer: Leader-Followers
- 3.4 Second layer: Drone-Leader
- 4 Results
- 4.1 Simulation results
- 4.2 Experimental results
- 5 Conclusion and future work
- Ref
Github: flyfly~~~
- 【Paper】2015_El H_Decentralized Control Architecture for UAV-UGV Cooperation
- 【Paper】2015_El H_UAV-UGV Cooperation For Objects Transportation In An Industrial Area
- 【Paper】2013_Double Exponential Smoothing for Predictive Vision Based Target Tracking
1 Introduction
1.1 Motivation and related works
Air-Ground Cooperation (AGC)
Unmanned Aerial Vehicles (UAVs)
Unmanned Ground Vehicles (UGVs)
1.2 Contribution and orgnization
The first contribution of our work consists in providing a real-time navigation scheme.
The second contribution concerns the visual-based formation.
2 Problem Statement
3 Architecture configuration
3.1 Hardware configuration
3.2 Overall architecture
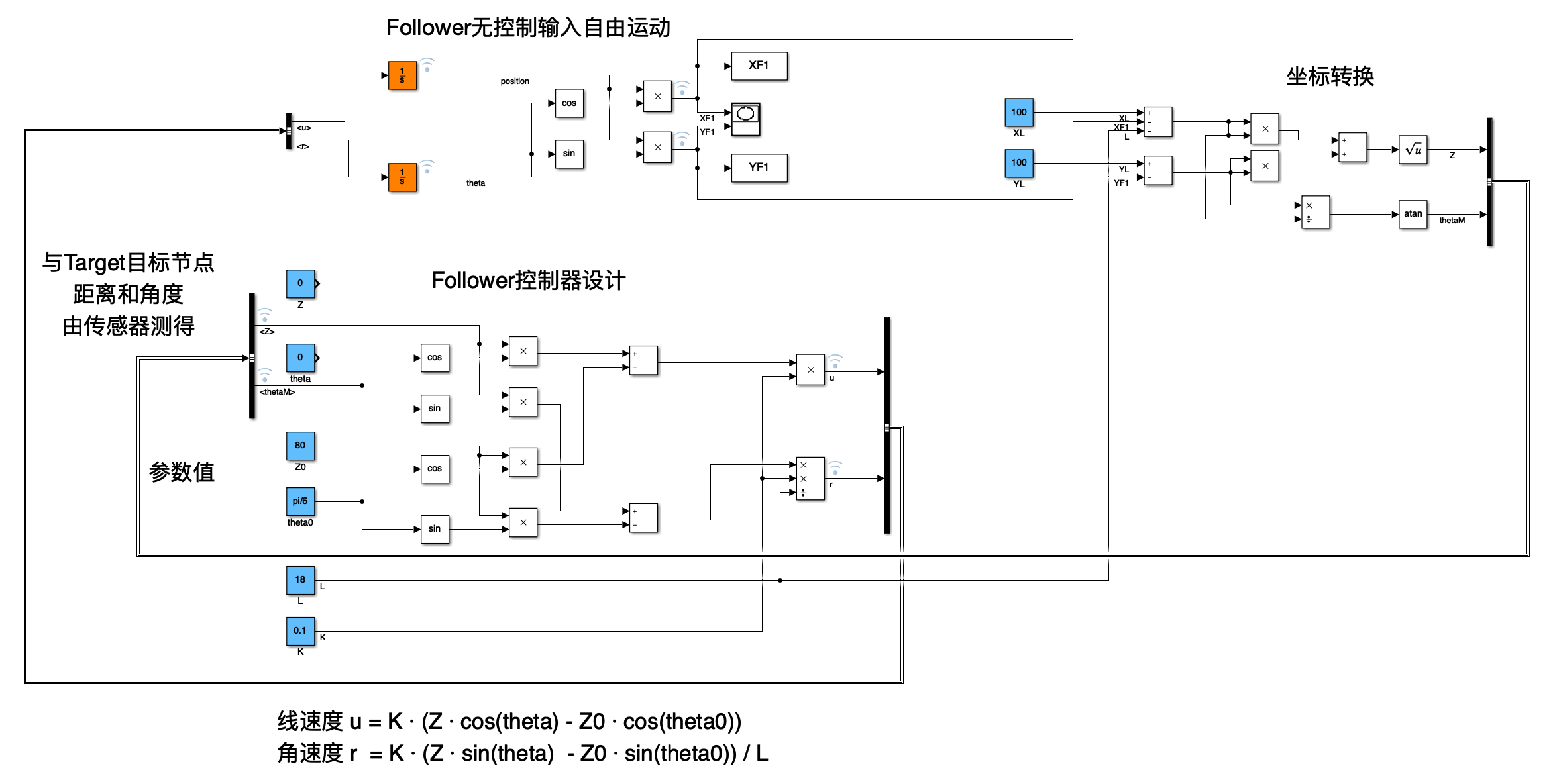
3.3 First layer: Leader-Followers
we consider the following errors
e
X
F
e_{XF}
eXF and
e
Y
F
e_{YF}
eYF corresponding to the differences between the initial and the tracking state:
e
X
F
=
z
⋅
cos
(
θ
)
−
z
0
⋅
cos
(
θ
0
)
e
Y
F
=
z
⋅
sin
(
θ
)
−
z
0
⋅
sin
(
θ
0
)
e_{XF} = zcdot cos(theta) - z_0 cdot cos(theta_0)\ e_{YF} = zcdot sin(theta) - z_0 cdot sin(theta_0)
eXF=z⋅cos(θ)−z0⋅cos(θ0)eYF=z⋅sin(θ)−z0⋅sin(θ0)
the time derivatives of
e
X
F
e_{XF}
eXF and
e
Y
F
e_{YF}
eYF :
e
˙
X
F
=
z
˙
⋅
cos
(
θ
)
−
z
⋅
θ
˙
⋅
sin
(
θ
)
e
Y
F
=
z
˙
⋅
sin
(
θ
)
−
z
⋅
θ
˙
⋅
cos
(
θ
)
dot e_{XF} = dot z cdot cos(theta) - z cdot dot theta cdot sin(theta) \ e_{YF} = dot z cdot sin(theta) - z cdot dot theta cdot cos(theta) \
e˙XF=z˙⋅cos(θ)−z⋅θ˙⋅sin(θ)eYF=z˙⋅sin(θ)−z⋅θ˙⋅cos(θ)
e ˙ X F = T V X F − u e ˙ Y F = T V Y F − r ⋅ L dot e_{XF} = TV_{XF} - u\ dot e_{YF} = TV_{YF} - rcdot L e˙XF=TVXF−ue˙YF=TVYF−r⋅L
e ˙ X F = − K ⋅ e X F e ˙ Y F = − K ⋅ e Y F dot e_{XF} = -K cdot e_{XF} \ dot e_{YF} = -K cdot e_{YF} e˙XF=−K⋅eXFe˙YF=−K⋅eYF
T V X F − u = − K ⋅ ( z ⋅ cos ( θ ) − z 0 ⋅ cos ( θ 0 ) ) T V Y F − r ⋅ L = − K ⋅ ( z ⋅ sin ( θ ) − z 0 ⋅ sin ( θ 0 ) ) TV_{XF} - u = -Kcdot (zcdot cos(theta) - z_0 cdot cos(theta_0))\ TV_{YF} - rcdot L = -Kcdot (zcdot sin(theta) - z_0 cdot sin(theta_0)) TVXF−u=−K⋅(z⋅cos(θ)−z0⋅cos(θ0))TVYF−r⋅L=−K⋅(z⋅sin(θ)−z0⋅sin(θ0))
Since the target’s velocities (
T
V
X
F
,
T
V
Y
F
TV_{XF},TV_{YF}
TVXF,TVYF) are unknown, we propose the following non-linear kinematic controller:
u
=
K
⋅
(
z
⋅
cos
(
θ
)
−
z
0
⋅
cos
(
θ
0
)
)
r
=
K
⋅
(
z
⋅
sin
(
θ
)
−
z
0
⋅
sin
(
θ
0
)
)
L
u = Kcdot (zcdot cos(theta) - z_0 cdot cos(theta_0)) \ r = frac{Kcdot (zcdot sin(theta) - z_0 cdot sin(theta_0))}{L}
u=K⋅(z⋅cos(θ)−z0⋅cos(θ0))r=LK⋅(z⋅sin(θ)−z0⋅sin(θ0))
Lyapunov candidate function:
V
=
e
X
F
2
+
e
Y
F
2
2
(
V
>
0
)
V
˙
=
e
X
F
⋅
e
˙
X
F
+
e
Y
F
⋅
e
˙
Y
F
V = frac{e_{XF}^2 + e_{YF}^2}{2}quad (V>0) \ dot V = e_{XF}cdot dot e_{XF} + e_{YF}cdot dot e_{YF}
V=2eXF2+eYF2(V>0)V˙=eXF⋅e˙XF+eYF⋅e˙YF
3.4 Second layer: Drone-Leader
4 Results
4.1 Simulation results
4.2 Experimental results
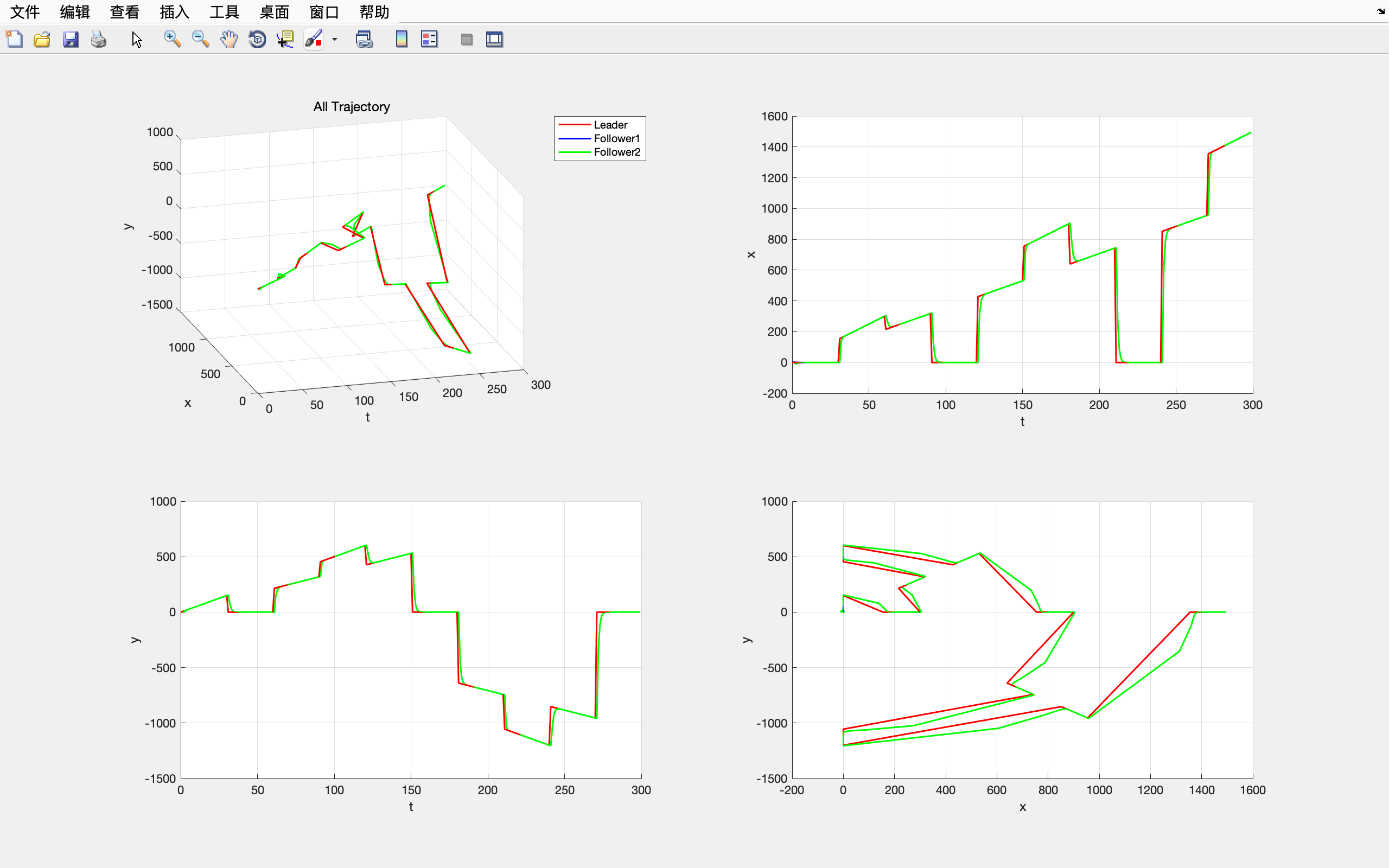
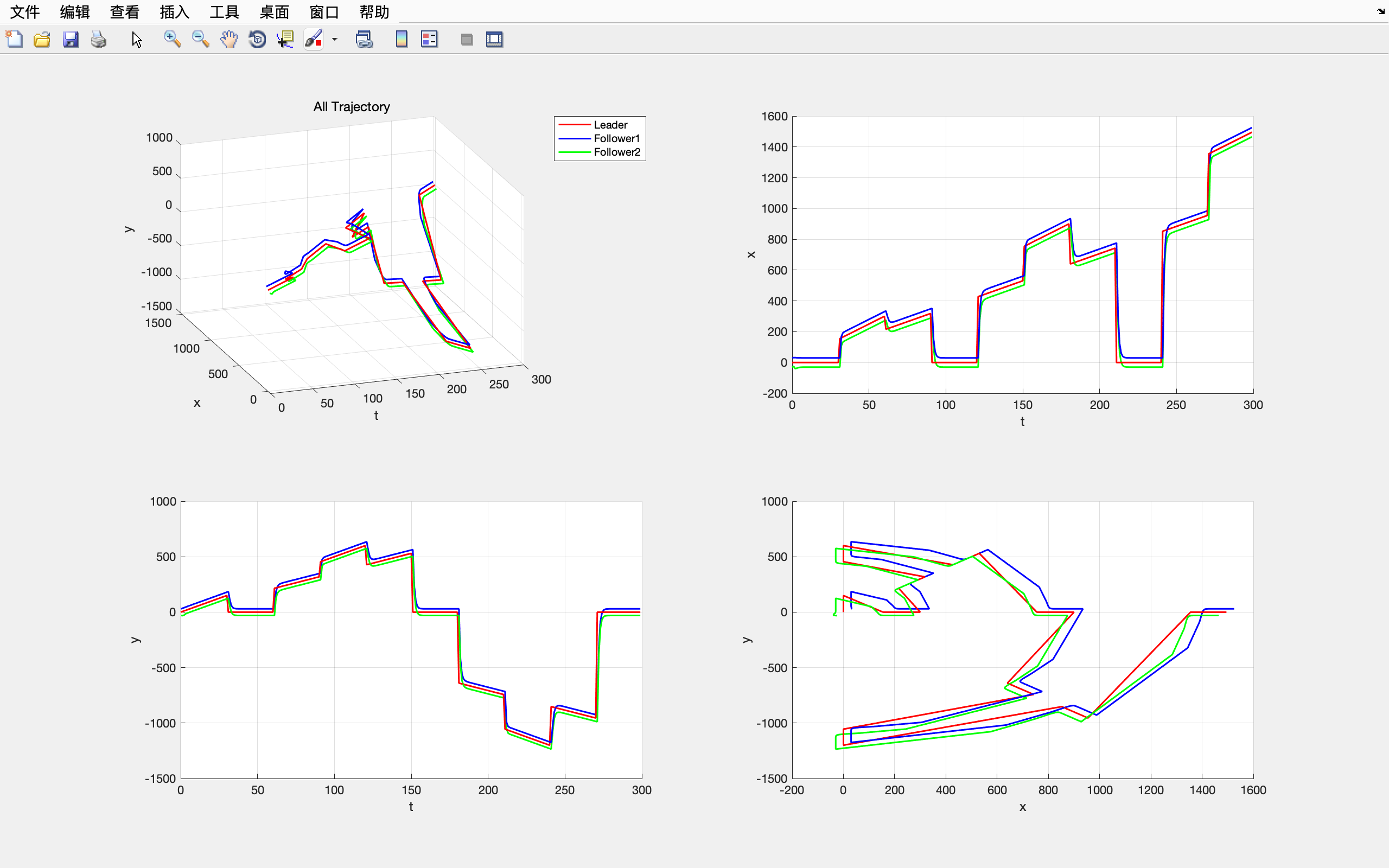
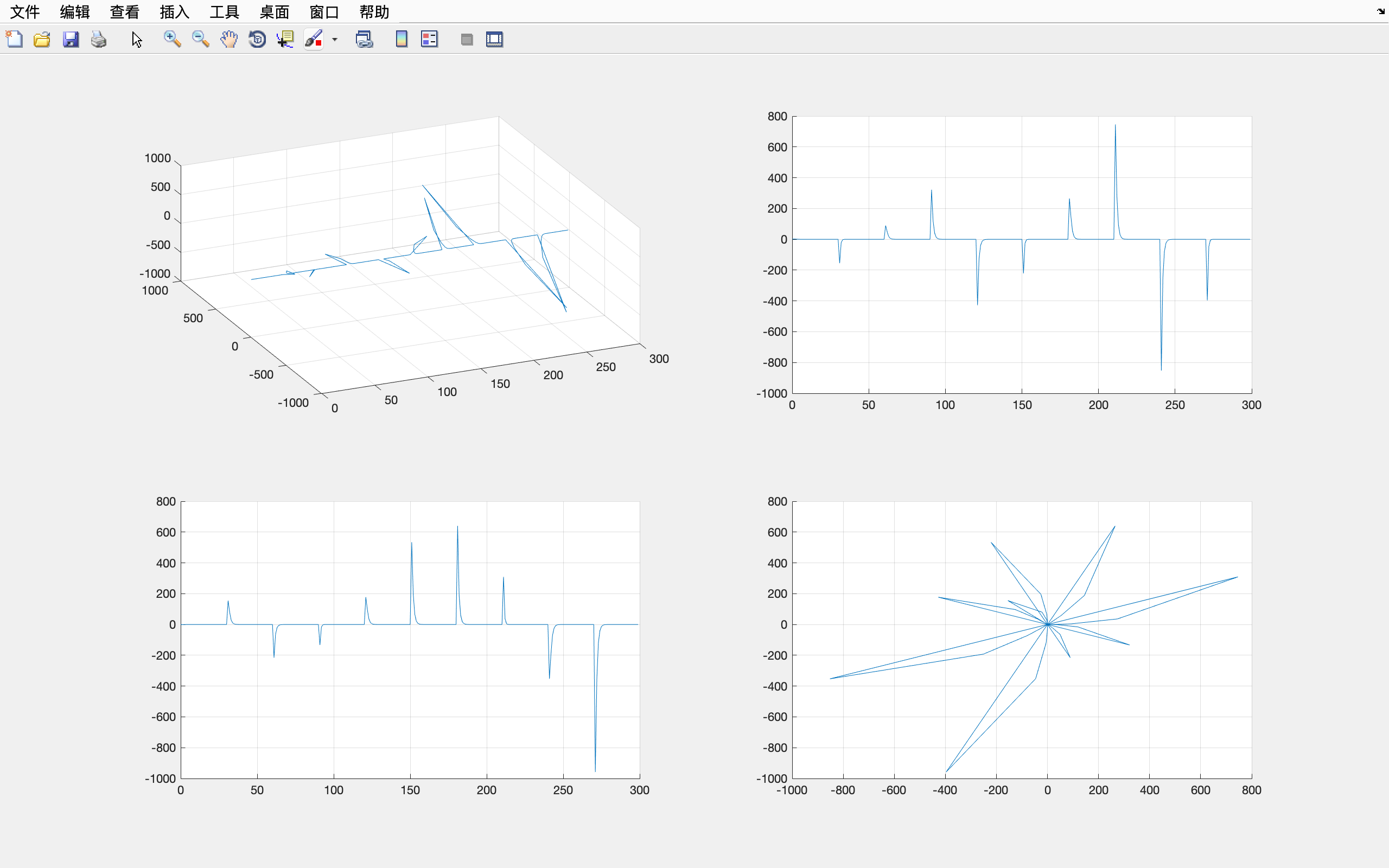

领航者轨迹仿真
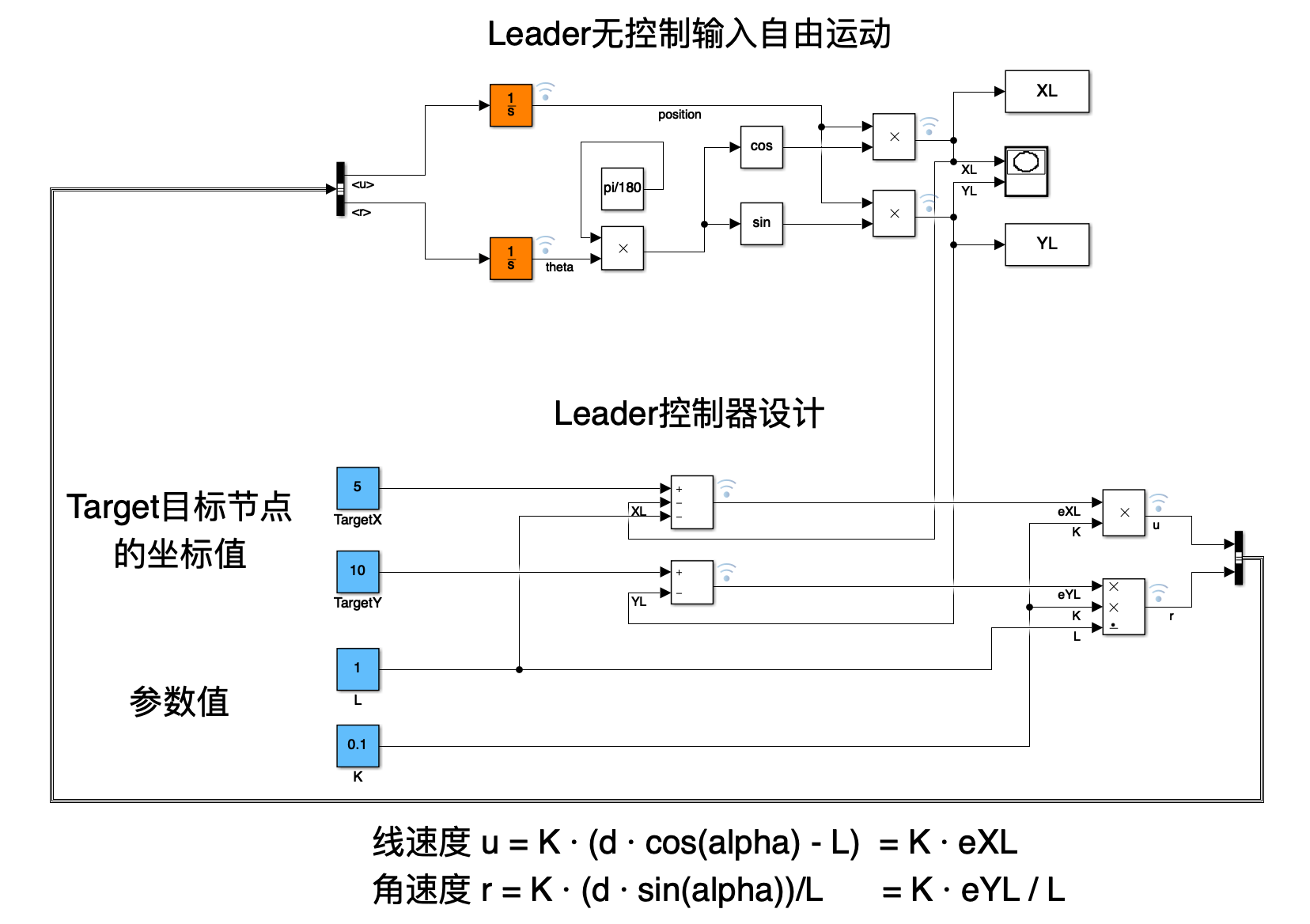
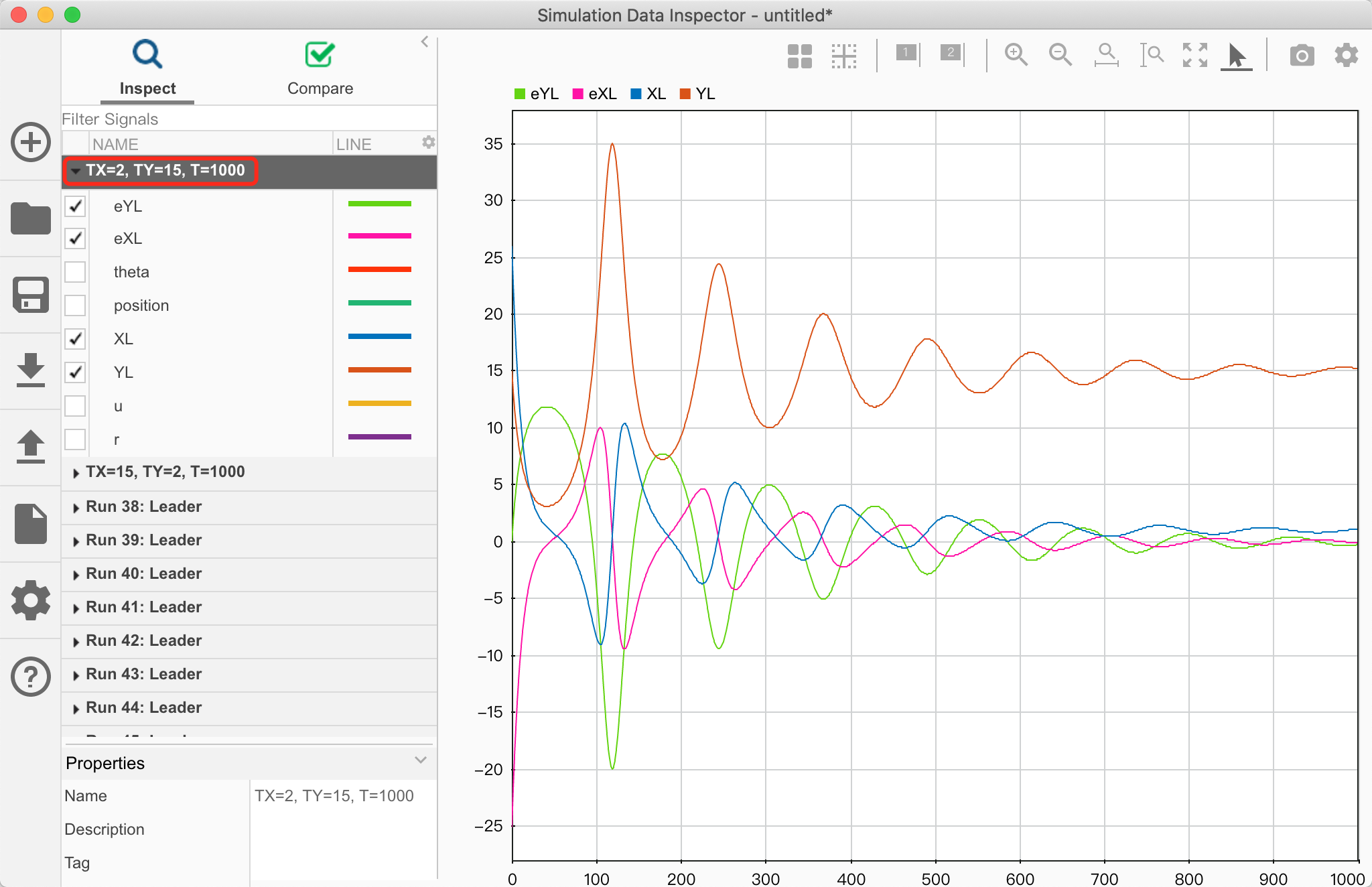
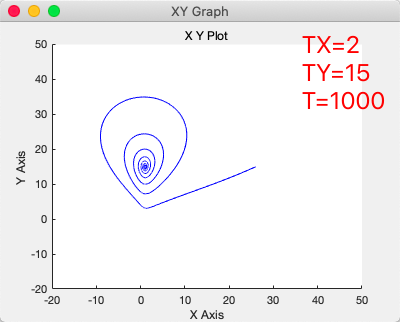
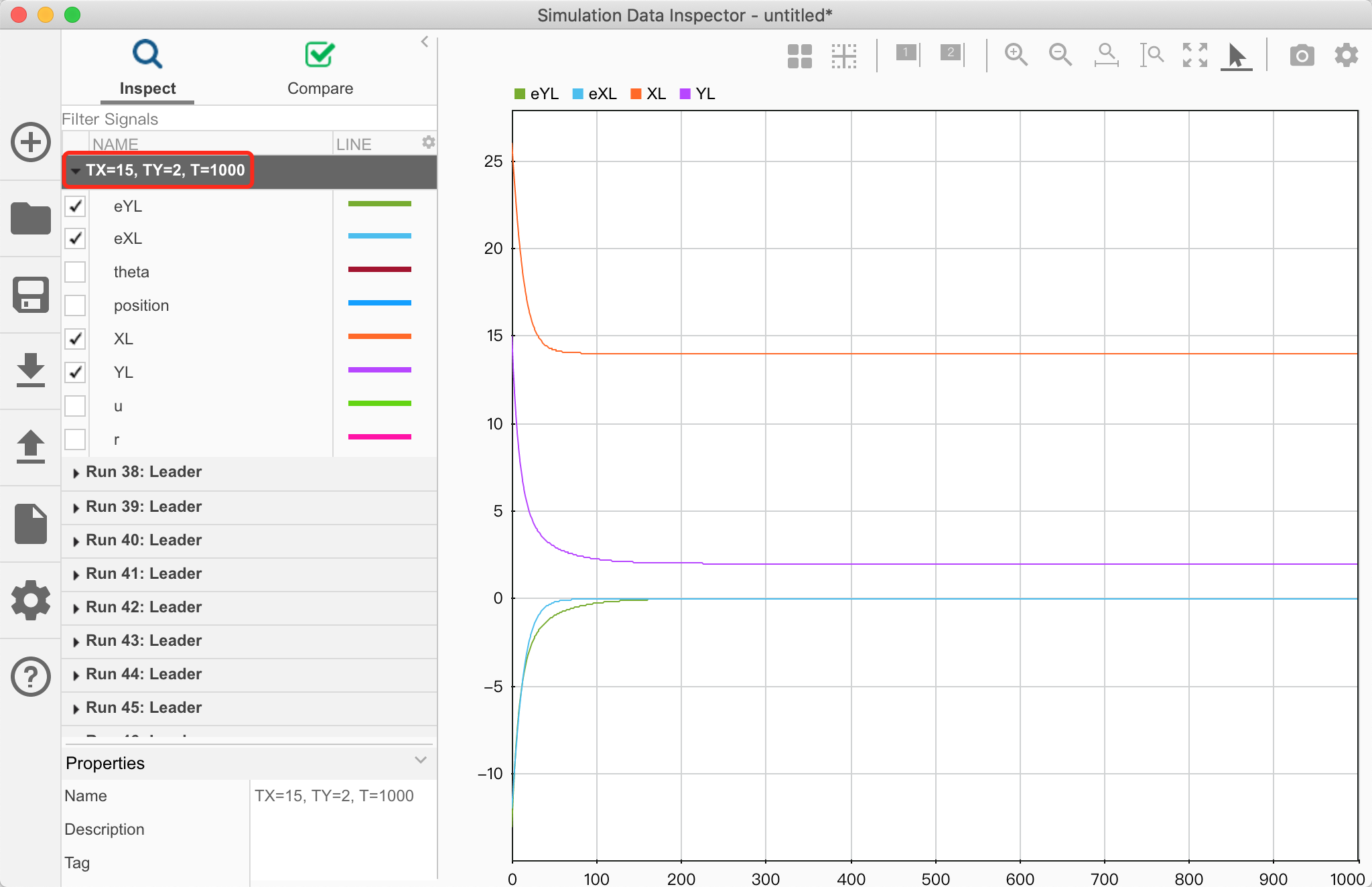
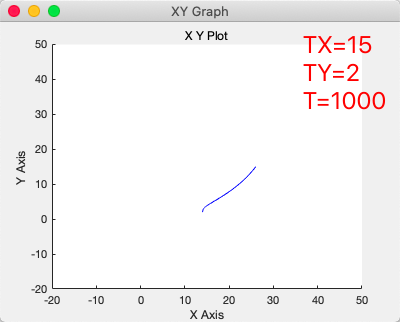
设置初始位置为
0
0
0,初始角度也为
0
0
0。
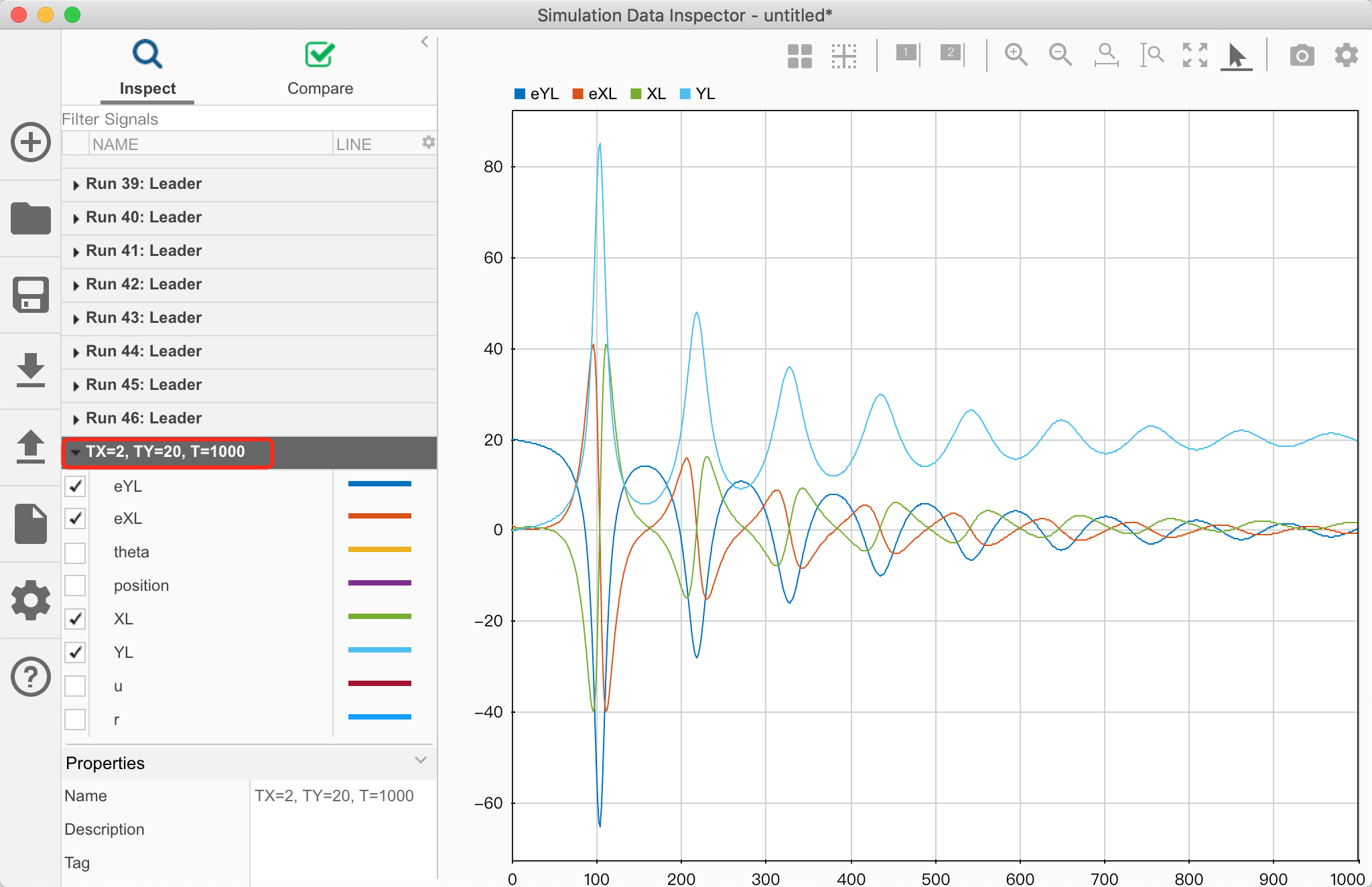
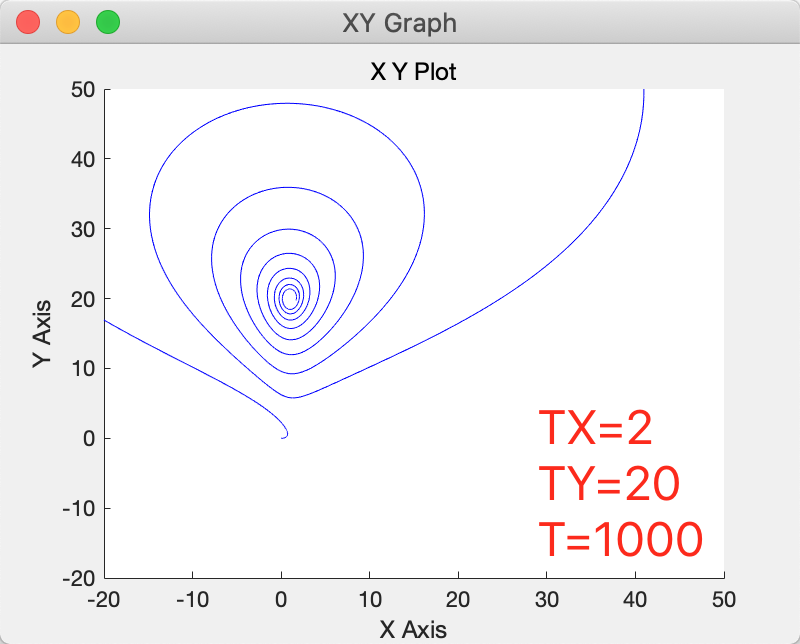
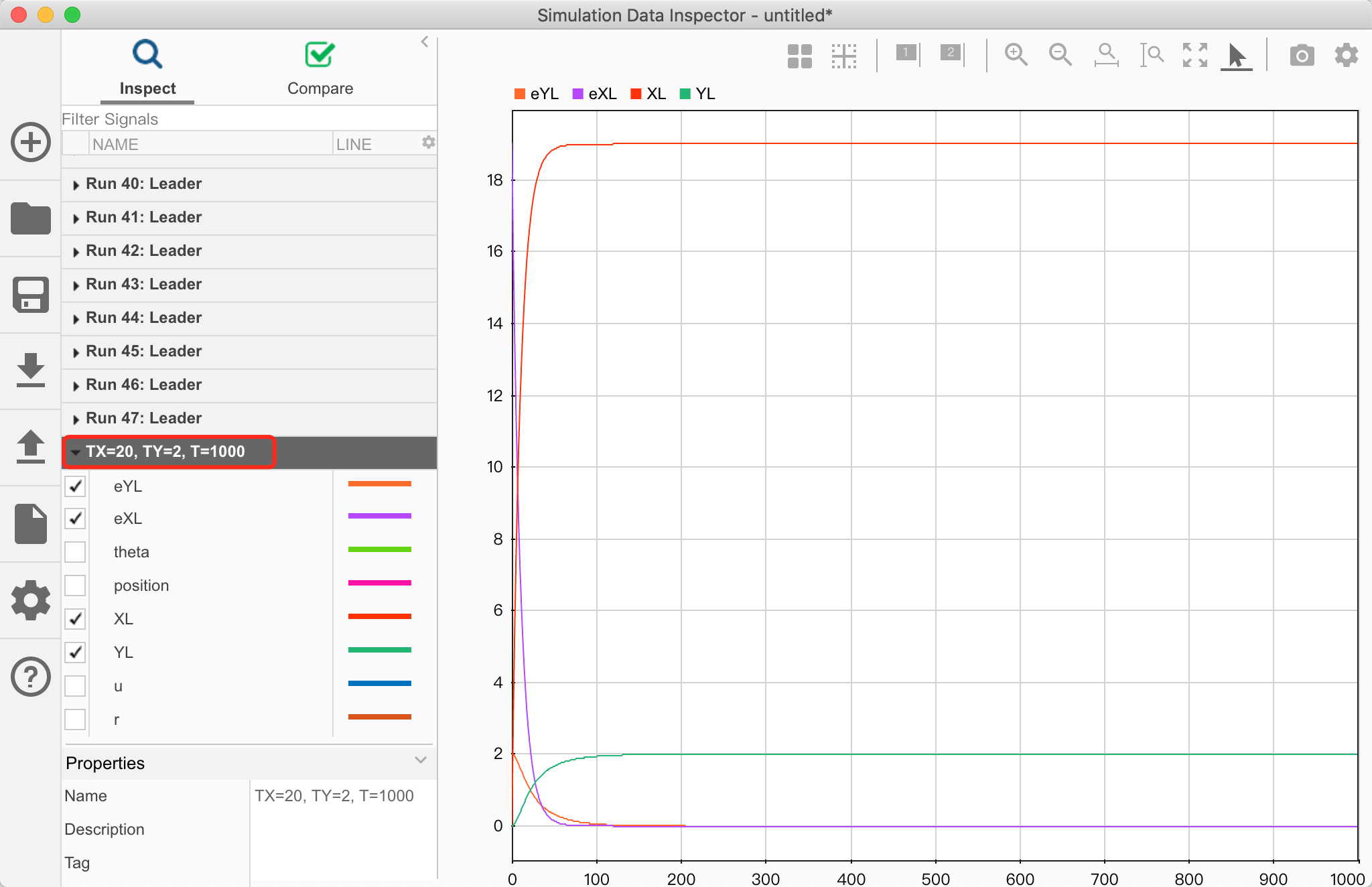
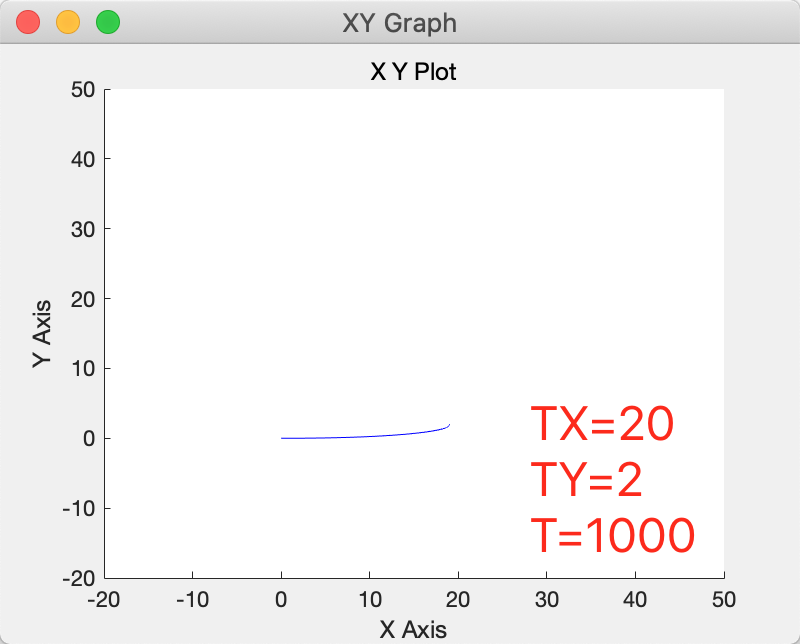
跟随者
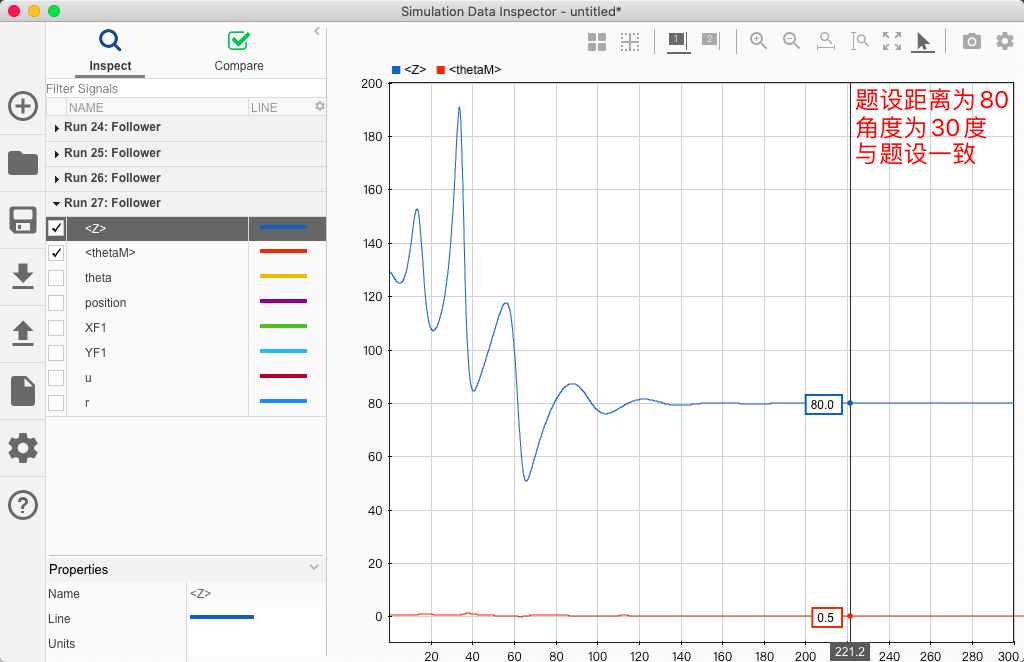
5 Conclusion and future work
Ref
Joseph J LaViola Jr. “an experiment comparing double exponential smoothing and kalman filter-based predictive tracking algorithms”. In Virtual Reality, 2003. Proceedings. IEEE, pages 283–284. IEEE, 2003.
最后
以上就是精明抽屉最近收集整理的关于【Paper】2015_El H_UAV-UGV Cooperation For Objects Transportation In An Industrial Area1 Introduction2 Problem Statement3 Architecture configuration4 Results5 Conclusion and future workRef的全部内容,更多相关【Paper】2015_El内容请搜索靠谱客的其他文章。








发表评论 取消回复