
【010】
一、求两数之和
给定一个整数数组 nums 和一个目标值 target,请你在该数组中找出和为目标值的那 两个 整数,并返回他们的数组下标。
你可以假设每种输入只会对应一个答案。但是,你不能重复利用这个数组中同样的元素。
示例:
给定 nums = [2, 7, 11, 15], target = 9
因为 nums[0] + nums[1] = 2 + 7 = 9
所以返回 [0, 1]方法一:暴力法
暴力法很简单。遍历每个元素 xx,并查找是否存在一个值与 target - xtarget−x 相等的目标元素。
public int[] twoSum(int[] nums, int target) {
for (int i = 0; i < nums.length; i++) {
for (int j = i + 1; j < nums.length; j++) {
if (nums[j] == target - nums[i]) {
return new int[] { i, j };
}
}
}
throw new IllegalArgumentException("No two sum solution");
}复杂度分析:
- 时间复杂度:O(n^2)O(n2), 对于每个元素,我们试图通过遍历数组的其余部分来寻找它所对应的目标元素,这将耗费 O(n)O(n) 的时间。因此时间复杂度为 O(n^2)O(n2)。
- 空间复杂度:O(1)O(1)。
方法二:两遍哈希表
为了对运行时间复杂度进行优化,我们需要一种更有效的方法来检查数组中是否存在目标元素。如果存在,我们需要找出它的索引。保持数组中的每个元素与其索引相互对应的最好方法是什么?哈希表。
通过以空间换取速度的方式,我们可以将查找时间从 O(n)O(n) 降低到 O(1)O(1)。哈希表正是为此目的而构建的,它支持以 近似 恒定的时间进行快速查找。我用“近似”来描述,是因为一旦出现冲突,查找用时可能会退化到 O(n)O(n)。但只要你仔细地挑选哈希函数,在哈希表中进行查找的用时应当被摊销为 O(1)O(1)。
一个简单的实现使用了两次迭代。在第一次迭代中,我们将每个元素的值和它的索引添加到表中。然后,在第二次迭代中,我们将检查每个元素所对应的目标元素(target - nums[i]target−nums[i])是否存在于表中。注意,该目标元素不能是 nums[i]nums[i] 本身!
public int[] twoSum(int[] nums, int target) {
Map<Integer, Integer> map = new HashMap<>();
for (int i = 0; i < nums.length; i++) {
map.put(nums[i], i);
}
for (int i = 0; i < nums.length; i++) {
int complement = target - nums[i];
if (map.containsKey(complement) && map.get(complement) != i) {
return new int[] { i, map.get(complement) };
}
}
throw new IllegalArgumentException("No two sum solution");
}复杂度分析:
- 时间复杂度:O(n)O(n), 我们把包含有 nn 个元素的列表遍历两次。由于哈希表将查找时间缩短到 O(1)O(1) ,所以时间复杂度为 O(n)O(n)。
- 空间复杂度:O(n)O(n), 所需的额外空间取决于哈希表中存储的元素数量,该表中存储了 nn 个元素。
方法三:一遍哈希表
事实证明,我们可以一次完成。在进行迭代并将元素插入到表中的同时,我们还会回过头来检查表中是否已经存在当前元素所对应的目标元素。如果它存在,那我们已经找到了对应解,并立即将其返回。
public int[] twoSum(int[] nums, int target) {
Map<Integer, Integer> map = new HashMap<>();
for (int i = 0; i < nums.length; i++) {
int complement = target - nums[i];
if (map.containsKey(complement)) {
return new int[] { map.get(complement), i };
}
map.put(nums[i], i);
}
throw new IllegalArgumentException("No two sum solution");
}复杂度分析:
- 时间复杂度:O(n)O(n), 我们只遍历了包含有 nn 个元素的列表一次。在表中进行的每次查找只花费 O(1)O(1) 的时间。
- 空间复杂度:O(n)O(n), 所需的额外空间取决于哈希表中存储的元素数量,该表最多需要存储 nn 个元素。
二、两数相加
给出两个 非空 的链表用来表示两个非负的整数。其中,它们各自的位数是按照 逆序 的方式存储的,并且它们的每个节点只能存储 一位 数字。
如果,我们将这两个数相加起来,则会返回一个新的链表来表示它们的和。
您可以假设除了数字 0 之外,这两个数都不会以 0 开头。
示例:
输入:(2 -> 4 -> 3) + (5 -> 6 -> 4)
输出:7 -> 0 -> 8
原因:342 + 465 = 807方法:初等数学
思路
我们使用变量来跟踪进位,并从包含最低有效位的表头开始模拟逐位相加的过程。
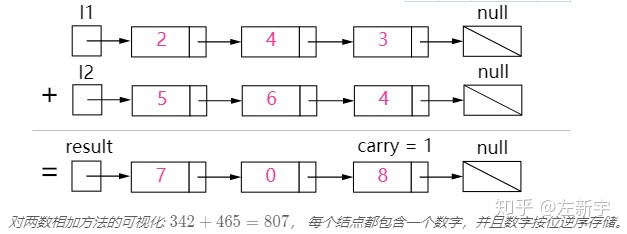
算法
就像你在纸上计算两个数字的和那样,我们首先从最低有效位也就是列表 l1l1 和 l2l2 的表头开始相加。由于每位数字都应当处于 0 ldots 90…9 的范围内,我们计算两个数字的和时可能会出现“溢出”。例如,5 + 7 = 125+7=12。在这种情况下,我们会将当前位的数值设置为 22,并将进位 carry = 1carry=1 带入下一次迭代。进位 carrycarry 必定是 00 或 11,这是因为两个数字相加(考虑到进位)可能出现的最大和为 9 + 9 + 1 = 199+9+1=19。
伪代码如下:
- 将当前结点初始化为返回列表的哑结点。
- 将进位 carrycarry 初始化为 00。
- 将 pp 和 qq 分别初始化为列表 l1l1 和 l2l2 的头部。
- 遍历列表 l1l1 和 l2l2 直至到达它们的尾端。
- 将 xx 设为结点 pp 的值。如果 pp 已经到达 l1l1 的末尾,则将其值设置为 00。
- 将 yy 设为结点 qq 的值。如果 qq 已经到达 l2l2 的末尾,则将其值设置为 00。
- 设定 sum = x + y + carrysum=x+y+carry。
- 更新进位的值,carry = sum / 10carry=sum/10。
- 创建一个数值为 (sum bmod 10)(summod10) 的新结点,并将其设置为当前结点的下一个结点,然后将当前结点前进到下一个结点。
- 同时,将 pp 和 qq 前进到下一个结点。
- 检查 carry = 1carry=1 是否成立,如果成立,则向返回列表追加一个含有数字 11 的新结点。
- 返回哑结点的下一个结点。
请注意,我们使用哑结点来简化代码。如果没有哑结点,则必须编写额外的条件语句来初始化表头的值。
请特别注意以下情况:

public ListNode addTwoNumbers(ListNode l1, ListNode l2) {
ListNode dummyHead = new ListNode(0);
ListNode p = l1, q = l2, curr = dummyHead;
int carry = 0;
while (p != null || q != null) {
int x = (p != null) ? p.val : 0;
int y = (q != null) ? q.val : 0;
int sum = carry + x + y;
carry = sum / 10;
curr.next = new ListNode(sum % 10);
curr = curr.next;
if (p != null) p = p.next;
if (q != null) q = q.next;
}
if (carry > 0) {
curr.next = new ListNode(carry);
}
return dummyHead.next;
}复杂度分析
- 时间复杂度:O(max(m, n))O(max(m,n)),假设 mm 和 nn 分别表示 l1l1 和 l2l2 的长度,上面的算法最多重复 max(m, n)max(m,n)次。
- 空间复杂度:O(max(m, n))O(max(m,n)), 新列表的长度最多为 max(m,n) + 1max(m,n)+1。
三、无重复字符的最长子串
给定一个字符串,请你找出其中不含有重复字符的 最长子串 的长度。
示例 1:
输入: "abcabcbb"
输出: 3
解释:因为无重复字符的最长子串是“abc”,所以其长度为3。
示例 2:
输入: "bbbbb"
输出: 1
解释:因为无重复字符的最长子串是“b”,所以其长度为1。
示例 3:
输入: "pwwkew"输出: 3
解释:因为无重复字符的最长子串是“wke”,所以其长度为3。
请注意:你的答案必须是子串的长度,“pwke”是一个子序列,不是子川串。
方法一:暴力法
思路
逐个检查所有的子字符串,看它是否不含有重复的字符。
算法
假设我们有一个函数 boolean allUnique(String substring) ,如果子字符串中的字符都是唯一的,它会返回true,否则会返回false。 我们可以遍历给定字符串 s 的所有可能的子字符串并调用函数 allUnique。 如果事实证明返回值为true,那么我们将会更新无重复字符子串的最大长度的答案。
现在让我们填补缺少的部分:
- 为了枚举给定字符串的所有子字符串,我们需要枚举它们开始和结束的索引。假设开始和结束的索引分别为 ii 和 jj。那么我们有 0 leq i lt j leq n0≤i<j≤n (这里的结束索引 jj 是按惯例排除的)。因此,使用 ii 从0到 n - 1n−1 以及 jj 从 i+1i+1 到 nn 这两个嵌套的循环,我们可以枚举出
s的所有子字符串。 - 要检查一个字符串是否有重复字符,我们可以使用集合。我们遍历字符串中的所有字符,并将它们逐个放入
set中。在放置一个字符之前,我们检查该集合是否已经包含它。如果包含,我们会返回false。循环结束后,我们返回true。
public class Solution {
public int lengthOfLongestSubstring(String s) {
int n = s.length();
int ans = 0;
for (int i = 0; i < n; i++)
for (int j = i + 1; j <= n; j++)
if (allUnique(s, i, j)) ans = Math.max(ans, j - i);
return ans;
}
public boolean allUnique(String s, int start, int end) {
Set<Character> set = new HashSet<>();
for (int i = start; i < end; i++) {
Character ch = s.charAt(i);
if (set.contains(ch)) return false;
set.add(ch);
}
return true;
}
}复杂度分析
- 时间复杂度:O(n^3)O(n3) 。
要验证索引范围在 [i, j)[i,j) 内的字符是否都是唯一的,我们需要检查该范围中的所有字符。 因此,它将花费 O(j - i)O(j−i) 的时间。
对于给定的i,对于所有 j in [i+1, n]j∈[i+1,n] 所耗费的时间总和为:
sum_{i+1}^{n}O(j - i)∑i+1nO(j−i)
因此,执行所有步骤耗去的时间总和为:
Oleft(sum_{i = 0}^{n - 1}left(sum_{j = i + 1}^{n}(j - i)right)right) = Oleft(sum_{i = 0}^{n - 1}frac{(1 + n - i)(n - i)}{2}right) = O(n^3)O(∑i=0n−1(∑j=i+1n(j−i)))=O(∑i=0n−12(1+n−i)(n−i))=O(n3) - 空间复杂度:O(min(n, m))O(min(n,m)),我们需要 O(k)O(k) 的空间来检查子字符串中是否有重复字符,其中 kk 表示
Set的大小。而 Set 的大小取决于字符串 nn 的大小以及字符集/字母 mm 的大小。
方法二:滑动窗口
算法
暴力法非常简单。但它太慢了。那么我们该如何优化它呢?
在暴力法中,我们会反复检查一个子字符串是否含有有重复的字符,但这是没有必要的。如果从索引 ii 到 j - 1j−1 之间的子字符串 s_{ij}sij 已经被检查为没有重复字符。我们只需要检查 s[j]s[j] 对应的字符是否已经存在于子字符串 s_{ij}sij 中。
要检查一个字符是否已经在子字符串中,我们可以检查整个子字符串,这将产生一个复杂度为 O(n^2)O(n2) 的算法,但我们可以做得更好。
通过使用 HashSet 作为滑动窗口,我们可以用 O(1)O(1) 的时间来完成对字符是否在当前的子字符串中的检查。
滑动窗口是数组/字符串问题中常用的抽象概念。 窗口通常是在数组/字符串中由开始和结束索引定义的一系列元素的集合,即 [i, j)[i,j)(左闭,右开)。而滑动窗口是可以将两个边界向某一方向“滑动”的窗口。例如,我们将 [i, j)[i,j) 向右滑动 11 个元素,则它将变为 [i+1, j+1)[i+1,j+1)(左闭,右开)。
回到我们的问题,我们使用 HashSet 将字符存储在当前窗口 [i, j)[i,j)(最初 j = ij=i)中。 然后我们向右侧滑动索引 jj,如果它不在 HashSet 中,我们会继续滑动 jj。直到 s[j] 已经存在于 HashSet 中。此时,我们找到的没有重复字符的最长子字符串将会以索引 ii 开头。如果我们对所有的 ii 这样做,就可以得到答案。
public class Solution {
public int lengthOfLongestSubstring(String s) {
int n = s.length();
Set<Character> set = new HashSet<>();
int ans = 0, i = 0, j = 0;
while (i < n && j < n) {
// try to extend the range [i, j]
if (!set.contains(s.charAt(j))){
set.add(s.charAt(j++));
ans = Math.max(ans, j - i);
}
else {
set.remove(s.charAt(i++));
}
}
return ans;
}
}复杂度分析
- 时间复杂度:O(2n) = O(n)O(2n)=O(n),在最糟糕的情况下,每个字符将被 ii 和 jj 访问两次。
- 空间复杂度:O(min(m, n))O(min(m,n)),与之前的方法相同。滑动窗口法需要 O(k)O(k) 的空间,其中 kk 表示
Set的大小。而Set的大小取决于字符串 nn 的大小以及字符集/字母 mm 的大小。
方法三:优化的滑动窗口
上述的方法最多需要执行 2n 个步骤。事实上,它可以被进一步优化为仅需要 n 个步骤。我们可以定义字符到索引的映射,而不是使用集合来判断一个字符是否存在。 当我们找到重复的字符时,我们可以立即跳过该窗口。
也就是说,如果 s[j]s[j] 在 [i, j)[i,j) 范围内有与 j'j′ 重复的字符,我们不需要逐渐增加 ii 。 我们可以直接跳过 [i,j'][i,j′] 范围内的所有元素,并将 ii 变为 j' + 1j′+1。
Java(使用 HashMap)
public class Solution {
public int lengthOfLongestSubstring(String s) {
int n = s.length(), ans = 0;
Map<Character, Integer> map = new HashMap<>(); // current index of character
// try to extend the range [i, j]
for (int j = 0, i = 0; j < n; j++) {
if (map.containsKey(s.charAt(j))) {
i = Math.max(map.get(s.charAt(j)), i);
}
ans = Math.max(ans, j - i + 1);
map.put(s.charAt(j), j + 1);
}
return ans;
}
}Java(假设字符集为 ASCII 128)
以前的我们都没有对字符串 s 所使用的字符集进行假设。
当我们知道该字符集比较小的时侯,我们可以用一个整数数组作为直接访问表来替换 Map。
常用的表如下所示:
int [26]用于字母 ‘a’ - ‘z’或 ‘A’ - ‘Z’int [128]用于ASCII码int [256]用于扩展ASCII码
public class Solution {
public int lengthOfLongestSubstring(String s) {
int n = s.length(), ans = 0;
int[] index = new int[128]; // current index of character
// try to extend the range [i, j]
for (int j = 0, i = 0; j < n; j++) {
i = Math.max(index[s.charAt(j)], i);
ans = Math.max(ans, j - i + 1);
index[s.charAt(j)] = j + 1;
}
return ans;
}
}复杂度分析
- 时间复杂度:O(n)O(n),索引 jj 将会迭代 nn 次。
- 空间复杂度(HashMap):O(min(m, n))O(min(m,n)),与之前的方法相同。
- 空间复杂度(Table):O(m)O(m),mm 是字符集的大小。
最后
以上就是勤恳菠萝最近收集整理的关于集合中元素相加为给定值的算法_三道基础算法题的全部内容,更多相关集合中元素相加为给定值内容请搜索靠谱客的其他文章。








发表评论 取消回复