2019杭电多校第九场 HDU 6682 Rikka with Mista

92 阅读 0 评论 61 点赞

我是靠谱客的博主粗心盼望，最近开发中收集的这篇文章主要介绍2019杭电多校第九场 HDU 6682 Rikka with Mista，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

在这里插入图片描述

题意

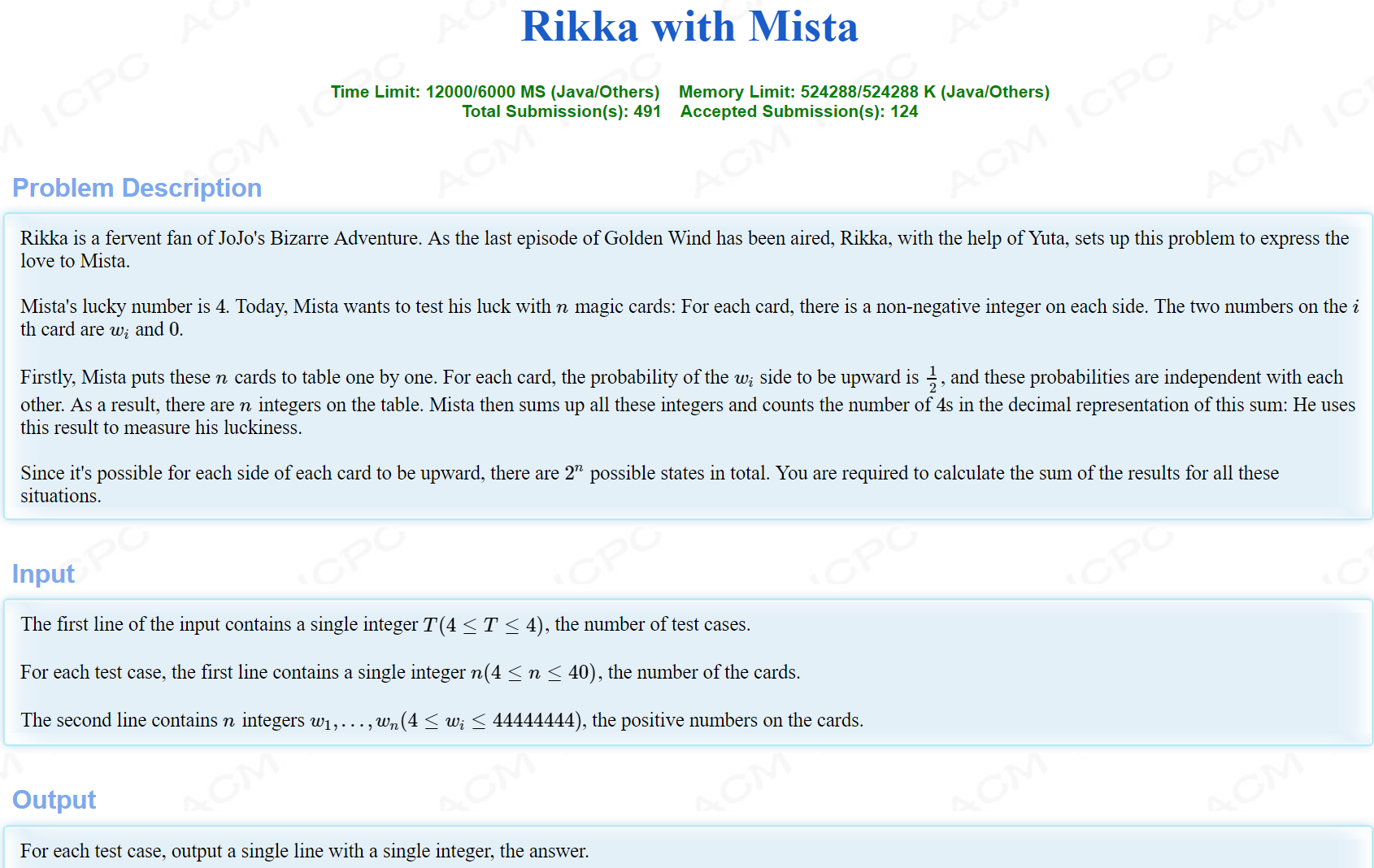
给出n个数，取任意个数加一起，将和的十进制表达中 4 的个数加到答案，问这 $2^n$ 个和的4的个数的和

题解

分别计算 $4times10^i$ 的答案
将一半的数放在A 中，另一半放在 B 中，分别暴力出所有组合
当 $(A_i+B_j) ~mod~10^{i+1}in[4times10^i,5times10^i)$ 时，答案加一
维持 A、B是有序的，所以可以用两个指针维护合法的区间
假设枚举的数字为 $x$ ，算出合法区间 $[n, m]$ ，然后让 $l$ 指向 $\geq n$ 的第一个数， $r$ 指向 $\geq m$ 的第一个数，那么 $r - l$ 就是答案
值得注意的是， $r - l$ 可能产生负数，我们规定，所有的位置都是在 $m o d l e n g h (B)$ 的意义下的，所以负数加上
$l e n g t h (B)$ 就可以了，基于此，所有的数组下标从 $0$ 开始，真的方便了好多

然后是如何维护有序
用归并排序就好了
因为，一开始要排次序，这就保证了对应位相同的数，他的下一位也是有序的，如此，满足归并排序的条件
自带 $inplace_merge(first,second,last)$ 函数

代码

#include<bits/stdc++.h>
#define N (1<<20)+3
#define LL long long
#define sc(x) scanf("%d",&x)
using namespace std;

int w[N],T,n,m,a,b,tot,l,r; 
int A[N],B[N],p4[10],p5[10],d[11],p[10];
int *c;
LL ans;

void dfs(int x,int y,int z){
    if (x==y){
        c[tot++]=z;
        return;
    }
    dfs(x+1,y,z+w[x]);
    dfs(x+1,y,z);
}

void merge(int *C,int c,int x){
    for(int i=0;i<11;i++) d[i]=c;
    for(int i=0;i<c;i++){
        int t=C[i]/p[x];
        if (d[t]==c) d[t]=i;
        C[i]%=p[x];
    }
    for(int i=9;i>=0;i--) if (d[i]==c) d[i]=d[i+1];
    for(int i=0;i<9;i++)
        inplace_merge(C,C+d[i+1],C+d[i+2]);
}

inline void mantain(int y,int x){
    int n=p4[x]-y,m=p5[x]-y-1;
    if (n<0) n+=p[x-1];
    if (m<0) m+=p[x-1];
    while(l<b&&B[l]<n) l++;
    while(l&&B[l-1]>=n) l--;
    while(r<b&&B[r]<=m) r++;
    while(r&&B[r-1]>m) r--;
}

void work(int x){
    l=r=0;
    for(int i=0;i<a;i++){
        mantain(A[i],x);
        ans+=r-l;
        if(r-l<0) ans+=b;
    }
    merge(A,a,x);
    merge(B,b,x);
}

int main(int argc, char const *argv[]){
    sc(T);
    while(T--){
        sc(n);
        for(int i=0;i<n;i++) sc(w[i]);
        
        c=A; tot=0; dfs(0,n/2,0); a=tot;
        c=B; tot=0; dfs(n/2,n,0); b=tot;

        sort(A,A+a); sort(B,B+b);

        ans=0;
        p[9]=1; for(int i=8;i>=0;i--) p[i]=p[i+1]*10;
        for(int i=1;i<10;i++) p4[i]=p[i]*4,p5[i]=p[i]*5;
        for(int i=1;i<10;i++) work(i);
        printf("%lldn",ans);
    }
    return 0;
}