「hdu6681」Rikka with Cake【线段树】

Rikka with Cake

Problem Description

Rikka’s birthday is on June $12-th$. The story of this problem happens on that day.

Today is $Rikk{a}^{\prime }s$ birthday. Yuta prepares a big cake for her: the shape of this cake is a rectangular of n centimeters times m centimeters. With the guidance of a grimoire, $Rikka$ is going to cut the cake.

For simplicity, $Rikka$ firstly builds a Cartesian coordinate system on the cake: the coordinate of the left bottom corner is $(0,0)$ while that of the right top corner is $(n,m)$. There are $K$ instructions on the grimoire: The $i-th$ cut is a ray starting from $(x_i,y_i)$ while the direction is $D_i$. There are four possible directions: $L$, passes $(x_{i-1},y_i)$; R, passes $(x_{i+1},y_i)$; U, passes $(x_i,y_{i+1})$; D, passes $(x_i,y_{i-1})$.

Take advantage of the infinite power of $Tyran{t}^{\prime }s$ Eye, $Rikka$ finishes all the instructions quickly. Now she wants to count the number of pieces of the cake. However, since a huge number of cuts have been done, the number of pieces can be very large. Therefore, $Rikka$ wants you to finish this task.

Input

The first line of the input contains a single integer $T(1\le T\le 100)$, the number of the test cases.

For each test case, the first line contains three positive integers $n,m,K(1\le n,m\le 10^9,1\le K\le 10^5)$, which represents the shape of the cake and the number of instructions on the grimoire.

Then $K$ lines follow, the ith line contains two integers $x_i,y_i(1\le x_i<n,1\le y_i<m)$ and a char D i ∈ { ′ L ′ , ′ R ′ , ′ U ′ , ′ D ′ } D_i∈{&#x27;L&#x27;,&#x27;R&#x27;,&#x27;U&#x27;,&#x27;D&#x27;} Di​∈{′L′,′R′,′U′,′D′}, which describes the ith cut.

The input guarantees that there are no more than 5 test cases with $K>1000$, and no two cuts share the same $x$ coordinate or $y$ coordinate, $i.e.,\forall 1\le i<j\le K,x_i!=x_{j}and{y}_i!=y_j.$

Output

For each test case, output a single line with a single integer, the number of pieces of the cake.

Hint

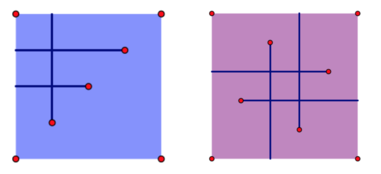
The left image and the right image show the results of the first and the second test case in the sample input respectively. Clearly, the answer to the first test case is $3$ while the second one is $5$.

Sample Input

2
4 4 3
1 1 U
2 2 L
3 3 L
5 5 4
1 2 R
3 1 U
4 3 L
2 4 D

Sample Output

3
5

Source

2019 Multi-University Training Contest 9

题意

• 就是给你一个$n\times m$的蛋糕，每次从蛋糕中间一个地方向四个方向中的一个方向切一刀【切的方向平行于其中一个蛋糕边缘】，问最后共几块蛋糕，没有切断的算一块

题解

• 比赛的时候一眼看出了答案是交点个数$+1$，和队友说了一下队友同意了，然后我这个伪几何选手直接套了一个线段交点个数的板子，这个板子是直接从网上搬过来的，表面看上去复杂度是$n\log n$，但是交上去$T$掉了，然后还是老老实实写线段树吧:(
• 先考虑向上切的与其他横切的交点个数，从上至下遍历所有横切的，在线段树中区间加值，然后对于一个向上切，单点查询值就是交点个数了，向下切在从下至上遍历一次就行了

代码

#pragma GCC optimize ("O3")
#include<bits/stdc++.h>

using namespace std;
const int maxn=2e5+10;

namespace IO{ 
    #define BUF_SIZE 100000 
    #define OUT_SIZE 100000 

    bool IOerror=0; 
    inline char nc(){ 
        static char buf[BUF_SIZE],*p1=buf+BUF_SIZE,*pend=buf+BUF_SIZE; 
        if (p1==pend){ 
            p1=buf; pend=buf+fread(buf,1,BUF_SIZE,stdin); 
            if (pend==p1){IOerror=1;return -1;} 
        } 
        return *p1++; 
    } 
    inline bool blank(char ch){return ch==' '||ch=='n'||ch=='r'||ch=='t';} 
    inline bool read(double &x){ 
        bool sign=0; char ch=nc(); x=0; 
        for (;blank(ch);ch=nc()); 
        if (IOerror) return false; 
        if (ch=='-')sign=1,ch=nc(); 
        for (;ch>='0'&&ch<='9';ch=nc())x=x*10+ch-'0'; 
        if (ch=='.'){ 
            double tmp=1; ch=nc(); 
            for (;ch>='0'&&ch<='9';ch=nc())tmp/=10.0,x+=tmp*(ch-'0'); 
        } 
        if (sign)x=-x; return true;
    } 
    template<typename T>
    inline bool read(T &x){ 
        bool sign=0; char ch=nc(); x=0; 
        for (;blank(ch);ch=nc()); 
        if (IOerror) return false; 
        if (ch=='-')sign=1,ch=nc(); 
        for (;ch>='0'&&ch<='9';ch=nc())x=x*10+ch-'0'; 
        if (sign)x=-x; return true;
    } 
    inline bool read(char *s){ 
        char ch=nc(); 
        for (;blank(ch);ch=nc()); 
        if (IOerror) return false; 
        for (;!blank(ch)&&!IOerror;ch=nc())*s++=ch; 
        *s=0; return true;
    } 
};
using namespace IO;

int sum[maxn<<2],mark[maxn<<2];

void down(int id)
{
    mark[id<<1]+=mark[id];mark[id<<1|1]+=mark[id];
    mark[id]=0;
}

void build(int id,int l,int r)
{
    mark[id]=0;
    if(l==r) return;
    int mid=(l+r)>>1;
    build(id<<1,l,mid);build(id<<1|1,mid+1,r);
}

void update(int id,int L,int R,int l,int r,long long add)
{
    if(l<=L&&R<=r) {
        mark[id]+=add;
        return;
    }
    if(mark[id]!=0) down(id);int mid=(L+R)>>1;
    if(l<=mid) update(id<<1,L,mid,l,r,add);
    if(r>mid) update(id<<1|1,mid+1,R,l,r,add);
}

int query(int id,int L,int R,int pos)
{
    if(L==R) return mark[id];
    int mid=(L+R)>>1;
    if(mark[id]) down(id);
    if(pos<=mid) return query(id<<1,L,mid,pos);
    else return query(id<<1|1,mid+1,R,pos);
}

struct line{
    int x,y,dir;
    line(int a=0,int b=0,int d=0) {
        x=a;y=b;dir=d;
    }
}a[maxn];

char s[10];
int b[maxn],c[maxn],w,h,n,m,k;
vector<int> vec[4][maxn];

void clear_()
{
    for(int i=0;i<=3;i++) for(int j=0;j<=h;j++) vec[i][j].clear();
}

int main()
{
    int t;read(t);
    while(t--) {
        read(n);read(m);read(k);
        for(int i=1,x,y;i<=k;i++) {
            read(a[i].x);read(a[i].y);read(s+1);
            b[i]=a[i].x;c[i]=a[i].y;
            if(s[1]=='L') a[i].dir=3;
            else if(s[1]=='R') a[i].dir=1;
            else if(s[1]=='U') a[i].dir=0;
            else a[i].dir=2;
        }
        sort(b+1,b+k+1);
        sort(c+1,c+k+1);

        w=unique(b+1,b+k+1)-b-1;
        h=unique(c+1,c+k+1)-c-1;
        for(int i=1;i<=k;i++) {
            a[i].x=lower_bound(b+1,b+k+1,a[i].x)-b;
            a[i].y=lower_bound(c+1,c+k+1,a[i].y)-c;
            vec[a[i].dir][a[i].y].push_back(a[i].x);

        }
        
        build(1,1,w);
        long long ans=0;
        for(int i=1;i<=h;i++) {
            for(auto j:vec[1][i]) update(1,1,w,j,w,1);
            for(auto j:vec[3][i]) update(1,1,w,1,j,1);

            for(auto j:vec[2][i]) ans+=query(1,1,w,j);
        }
        build(1,1,w);
        for(int i=h;i>=1;i--) {
            for(auto j:vec[1][i]) update(1,1,w,j,w,1);
            for(auto j:vec[3][i]) update(1,1,w,1,j,1);
            for(auto j:vec[0][i]) ans+=query(1,1,w,j);
        }
        printf("%lldn",ans+1);

        clear_();
    }
}

最后

以上就是苗条舞蹈为你收集整理的「hdu6681」Rikka with Cake【线段树】的全部内容，希望文章能够帮你解决「hdu6681」Rikka with Cake【线段树】所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。