概述
There are n rectangles on the plane. The problem is to find the area of the union of these rectangles. Note that these rectangles might overlap with each other, and the overlapped areas of these rectangles shall not be counted more than once. For example, given a rectangle A with the bottom left corner located at (0,0) and the top right corner at (2,2), and the other rectangle B with the bottom left corner located at (1,1) and the top right corner at (3,3), it follows that the area of the union of A and B should be 7, instead of 8.
Although the problem looks simple at the first glance, it might take a while to figure out how to do it correctly. Note that the shape of the union can be very complicated, and the intersected areas can be overlapped by more than two rectangles.
Note:
(1) The coordinates of these rectangles are given in integers. So you do not have to worry about the floating point round-off errors. However, these integers can be as large as 1,000,000.
(2) To make the problem easier, you do not have to worry about the sum of the areas exceeding the long integer precision. That is, you can assume that the total area does not result in integer overflow.
Input Format
Several sets of rectangles configurations. The inputs are a list of integers. Within each set, the first integer (in a single line) represents the number of rectangles, n, which can be as large as 1000. After n, there will be n lines representing the n rectangles; each line contains four integers <a,b,c,d> , which means that the bottom left corner of the rectangle is located at (a,b), and the top right corner of the rectangle is located at (c,d). Note that integers a, b, c, d can be as large as 1,000,000.
These configurations of rectangles occur repetitively in the input as the pattern described above. An integer n=0 (zero) signifies the end of input.
Output Format
For each set of the rectangles configurations appeared in the input, calculate the total area of the union of the rectangles. Again, these rectangles might overlap each other, and the intersecting areas of these rectangles can only be counted once. Output a single star '*' to signify the end of outputs.
样例输入
2 0 0 2 2 1 1 3 3 3 0 0 1 1 2 2 3 3 4 4 5 5 0
样例输出
7 3 *
题目大意：
给你几个矩形的左下角坐标和右上角坐标，让你求出这些矩形并集的面积（就是矩形所占用的全部面积，重合的部分只算一次）；
解题思路：
1.先利用结构体存储每个矩形的坐标；
2.然后自后向前搜索每个矩形；
3.将当前矩形与之前搜索过的矩形进行比较（第n-1个与第n个比较，第n-2与n-1与n个比较，以此类推）；
比较方式采用切割的方法：
例如：新矩形x1是在老矩形x1'的左边，就可以以x1'这条边对新矩形进行切割，切割出的部分便是需要加到总面积的部分；
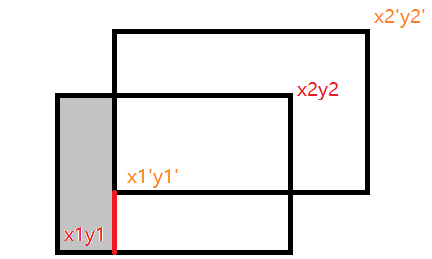
代码如下：
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<iostream>
#include<string>
#include<vector>
#include<stack>
#include<bitset>
#include<cstdlib>
#include<cmath>
#include<set>
#include<list>
#include<deque>
#include<map>
#include<queue>
using namespace std;
struct node
{
long long int x1,x2,y1,y2;
}T[1010];//结构体存矩形数据
int n=0;
long long int sum[1010];//用以存储每个矩形多出来的面积
void find(long long int x1,long long int y1,long long int x2,long long int y2,int k,int c)
{
/*此函数用于寻找新矩形比老矩形多出来的面积
开始的while循环用来排除掉不重合的老矩形 */
while(k<n&&(x1>=T[k].x2||x2<=T[k].x1||y1>=T[k].y2||y2<=T[k].y1))
k++;
if(k>=n)
{
sum[c]+=(x2-x1)*(y2-y1);
return;//切割出来的矩形计算面积加入当前矩形多余面积和中
}
/*下面几条判断语句用用来逐个切割矩形
具体切割方式见上方图片解释
*/
if(x1<T[k].x1)
{
find(x1,y1,T[k].x1,y2,k+1,c);/*将切割的新矩形与更上一个老矩形比较，
最后有一个最终切割面不与任何矩形重合
下面几组判断同理*/
x1=T[k].x1;
}
if(x2>T[k].x2)
{
find(T[k].x2,y1,x2,y2,k+1,c);
x2=T[k].x2;
}
if(y1<T[k].y1)
{
find(x1,y1,x2,T[k].y1,k+1,c);
y1=T[k].y1;
}
if(y2>T[k].y2)
{
find(x1,T[k].y2,x2,y2,k+1,c);
y2=T[k].y2;
}
}
int main()
{
int i;
long long int x1,x2,y1,y2;
while(cin>>n)
{
if(n==0)
{
cout<<"*"<<endl;
break;
}
for(int j=0;j<n;j++)
{
scanf("%lld%lld%lld%lld",&x1,&y1,&x2,&y2);
T[j].x1=x1,T[j].y1=y1;
T[j].x2=x2,T[j].y2=y2;
sum[j]=0;
}
for(i=n-1;i>=0;i--)
find(T[i].x1,T[i].y1,T[i].x2,T[i].y2,i+1,i);//自后向前逐个扫描矩形
long long int ans=0;
for(i=0;i<n;i++)
ans+=sum[i];//将所有切割面积加起来
printf("%lldn",ans);
}
return 0;
}
没什么特别注意的，可能数精度会很高我用了long long其他没什么了；
最后
以上就是欢呼百合为你收集整理的Overlapping Rectangles的全部内容，希望文章能够帮你解决Overlapping Rectangles所遇到的程序开发问题。
如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。
发表评论 取消回复