无向图最短路径的数目

转载自http://www.cnblogs.com/AndyJee/p/4640508.html
题目：
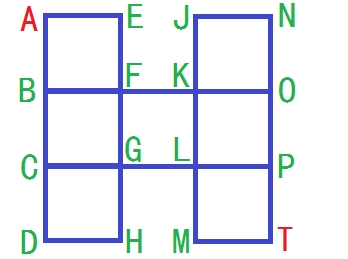
给定如下图所示的无向连通图，假定图中所有边的权值都为1；
显然，从源点A到终点T的最短路径有多条，求不同的最短路径的数目。
注：两条路径中有任意结点不同或者结点顺序不同，都称为不同的路径。

思路：
给定的图中，边权相等且非负，Dijkstra最短路径算法退化为BFS广度优先搜索。实现过程中可以使用队列。
计算到某结点最短路径条数，只需计算与该结点相邻的结点的最短路径值和最短路径条数，把最短路径值最小且相等的最短路径条数加起来即可。

答案：12

#include <iostream>
#include <queue>
#include <string.h>
using namespace std;
const int N=16;
int calNumOfPath(int G[N][N]){
int stepNum[N]; // how many steps to reach i
int pathNum[N]; // how many paths can reach i
bool visited[N];
memset(stepNum,0,N*sizeof(int));
memset(pathNum,0,N*sizeof(int));
memset(visited,false,N*sizeof(bool));
stepNum[0]=0;
pathNum[0]=1;
queue<int> q;
q.push(0);
while(!q.empty()){
int node=q.front();
q.pop();
visited[node]=true;
int s=stepNum[node]+1;
for(int i=0;i<N;i++){
if(i!=node && !visited[i] && G[node][i]==1){
if(stepNum[i]==0 || pathNum[i]>s){
stepNum[i]=s;
pathNum[i]=pathNum[node];
q.push(i);
}
else if(stepNum[i]==s){
pathNum[i]=pathNum[i]+pathNum[node];
}
}
}
}
return pathNum[N-1];
}
int main()
{
int G[16][16]={
{0,1,0,0,1,0,0,0,0,0,0,0,0,0,0,0},
{1,0,1,0,0,1,0,0,0,0,0,0,0,0,0,0},
{0,1,0,1,0,0,1,0,0,0,0,0,0,0,0,0},
{0,0,1,0,0,0,0,1,0,0,0,0,0,0,0,0},
{1,0,0,0,0,1,0,0,0,0,0,0,0,0,0,0},
{0,1,0,0,1,0,1,0,0,1,0,0,0,0,0,0},
{0,0,1,0,0,1,0,1,0,0,1,0,0,0,0,0},
{0,0,0,1,0,0,1,0,0,0,0,0,0,0,0,0},
{0,0,0,0,0,0,0,0,0,1,0,0,1,0,0,0},
{0,0,0,0,0,1,0,0,1,0,1,0,0,1,0,0},
{0,0,0,0,0,0,1,0,0,1,0,1,0,0,1,0},
{0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,1},
{0,0,0,0,0,0,0,0,1,0,0,0,0,1,0,0},
{0,0,0,0,0,0,0,0,0,1,0,0,1,0,1,0},
{0,0,0,0,0,0,0,0,0,0,1,0,0,1,0,1},
{0,0,0,0,0,0,0,0,0,0,0,1,0,0,1,0}};
cout << calNumOfPath(G) << endl;
return 0;
}

最后

以上就是痴情萝莉为你收集整理的无向图最短路径的数目的全部内容，希望文章能够帮你解决无向图最短路径的数目所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。