PBR来龙去脉十：低差异序列开头

今天来看PBRT第七章。

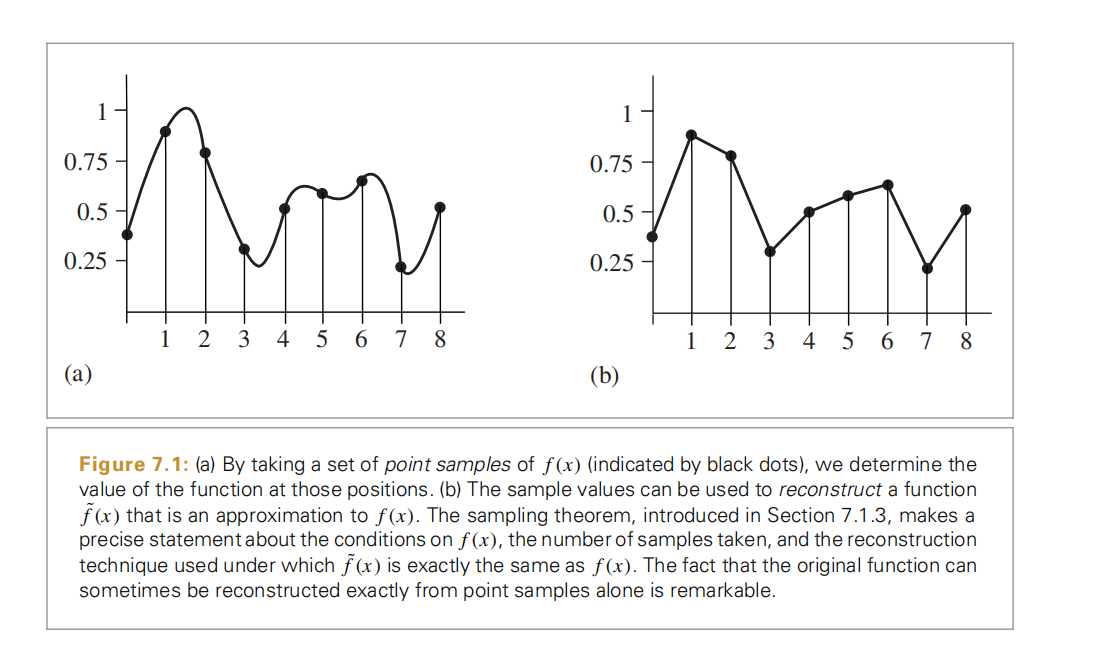
这里的采样定理把所有图像源作为原始函数，而最终显示器上的值为重建后的函数。取一组样本值并将它们转化为连续函数的过程叫做重建。

这里要注意，光线追踪算法的渲染过程并不是单纯的把目标的像素值从原始的像素值直接拷贝过来，后面需要根据采样的定理来理解这个差别。

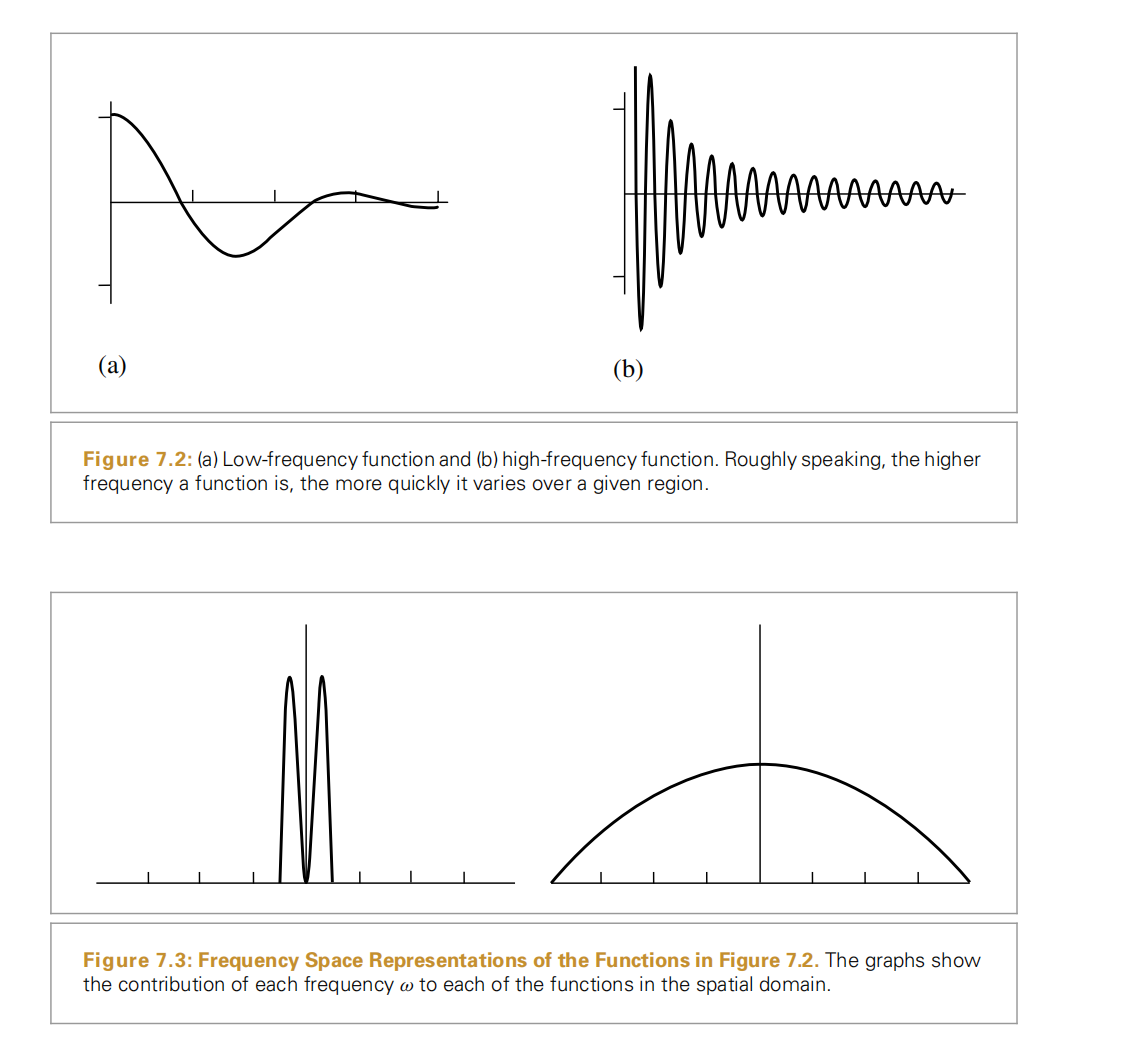
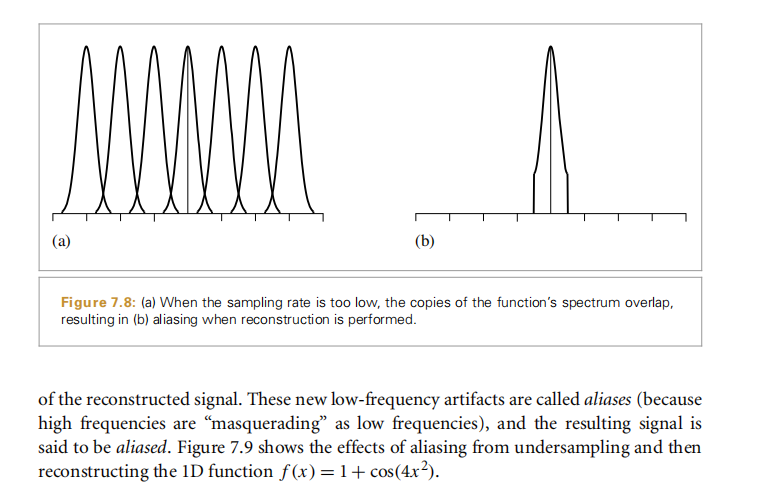
采样和重构过程使用了近似技术，这就会出现所谓“走样”(aliasing)的失真现象，这种失真会有多种情况，其中包括锯齿边和动画中的闪烁现象。失真现象的出现是因为采样过程并不能够获取连续图像函数的全部信息。 

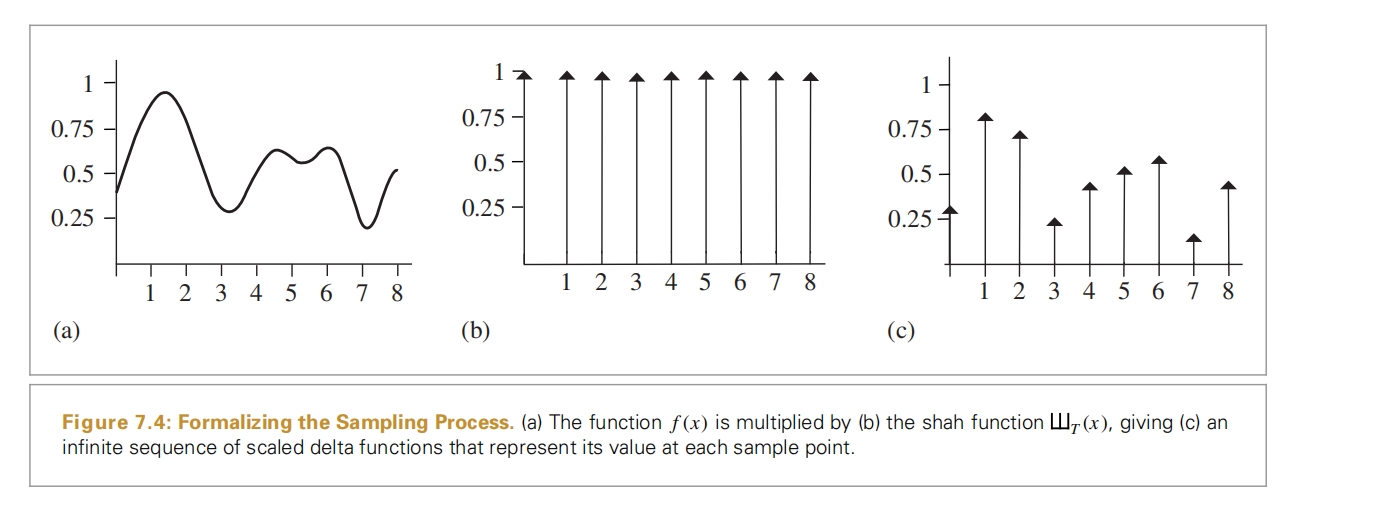
 这里要好好理解下，首先十山t(x)，通过x-iT，我们知道间隔是T，然后是前面有个系数T，

 目前还是理解不了，看后面有没有解释吧。不过现在有一个现象，

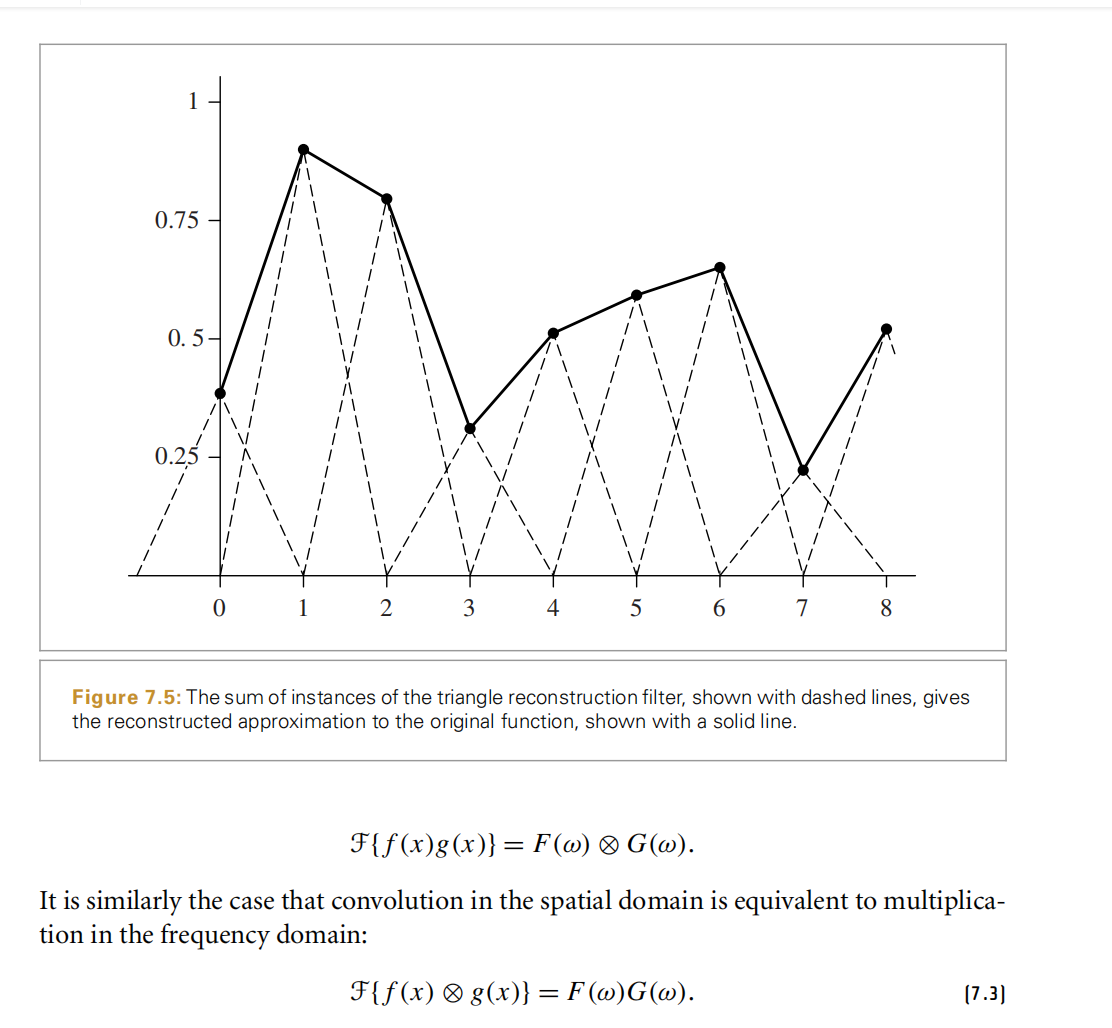
上面是卷积定理。

这里也非常有意思，时域中周期为T的函数，在频域中的周期就是1/T

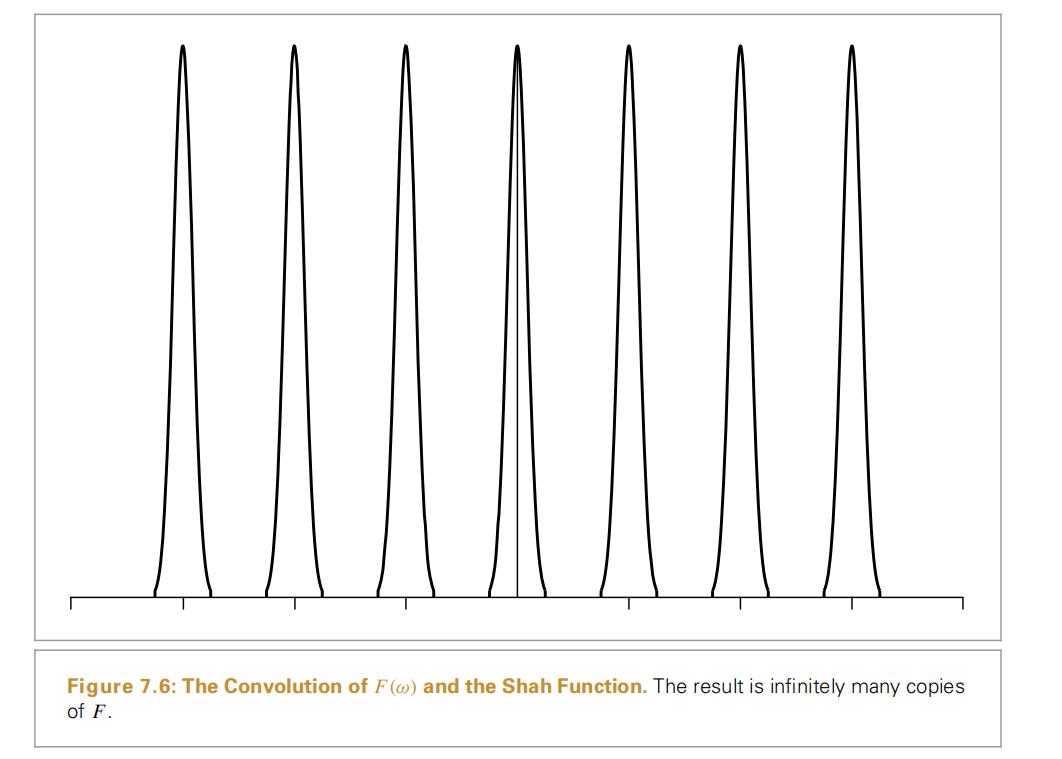 而采样函数的乘积对应的就是频域的卷积，也就是

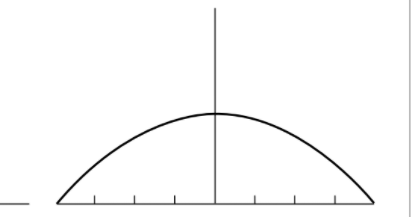
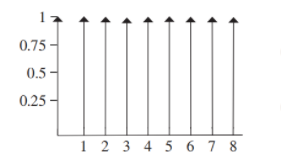
 这种函数的卷积的意思就是函数的不断重复的过程，也就是：

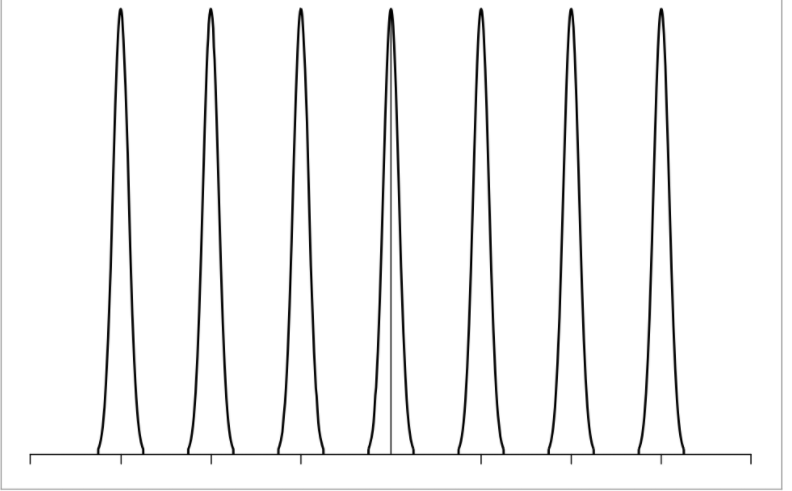
根据卷积的定义应该更好理解：

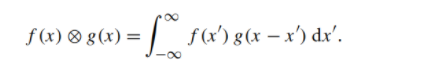
 首先f(x')是这个函数的采样值，因为积分域是无穷，所以可以还原出原始信号f(x),然后他要和g(x-x')先进行乘积再积分，积分就是求和，我们把所有x的值取边，然后相加就行。

具体还是要看下文章：https://zhuanlan.zhihu.com/p/103730714

所以直接从离散的卷积定义其实就可以看出来：

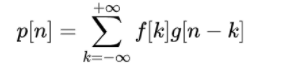
不过要理解频域卷积，还是得看这篇文章：https://blog.csdn.net/qq_37335890/article/details/84922878

傅里叶变换推导部分，可以看：https://zhuanlan.zhihu.com/p/41455378（注意看评论区，因为原文有错误）

不过这里的频移性质是e^jwt，似乎和我们想要的脉冲函数没啥关系。但其实e^jwt的傅里叶就是脉冲函数。

参考：https://www.zhihu.com/question/20973620

 于是，我们知道了e^iwj的傅里叶就是一个脉冲函数。

单个脉冲函数的傅里叶变换：https://zhuanlan.zhihu.com/p/108271985

那么shah函数的傅里叶变换推导：https://www.thefouriertransform.com/pairs/shah.php

这里一开始我没有反应过来，为什么必须先傅里叶级数一下再推导，而直接带入傅里叶变换公式不行，后来我发现了，如果是周期函数，傅里叶的积分域是一个周期内的，所以带入傅里叶公式后，

其实只需要取某个周期的狄拉克函数，当然这样推到起来就没有傅里叶级数带入来的快了。

大佬说可以直接根据泊松求和公式，泊松求和公式证明：https://zhuanlan.zhihu.com/p/107540842

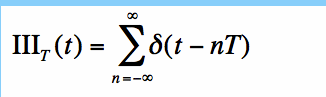
所以，f就是狄拉克函数，f的傅里叶是求和e^-iwnT 

不过这个求和其实就是狄拉克函数本身。

 让我们回到教材本身：

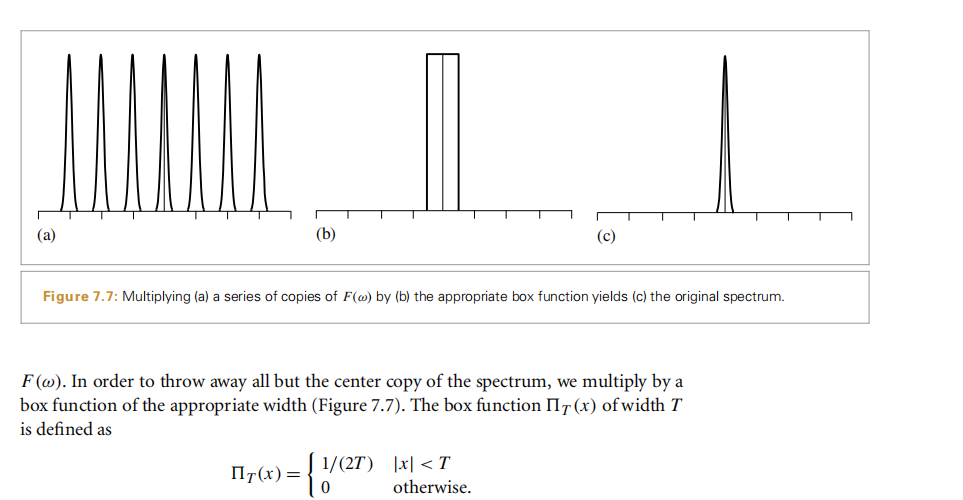
 这里可以看到无法完美重建的原因，首先完美重建基于的是公式：

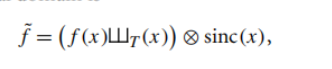
假定f(x)已知，那么似乎是可以根据公式完美重建的，但实际上，我们得到的是一堆采样值，也就是f(i)，而这些采样值要完美还原信号，只能通过无穷个求和，这是无法实际操作的。

这里提到了卷积定理，卷积定理证明：https://blog.csdn.net/xxmy7/article/details/109358114

然后是采样定理证明：https://blog.csdn.net/qq_35771020/article/details/83959339

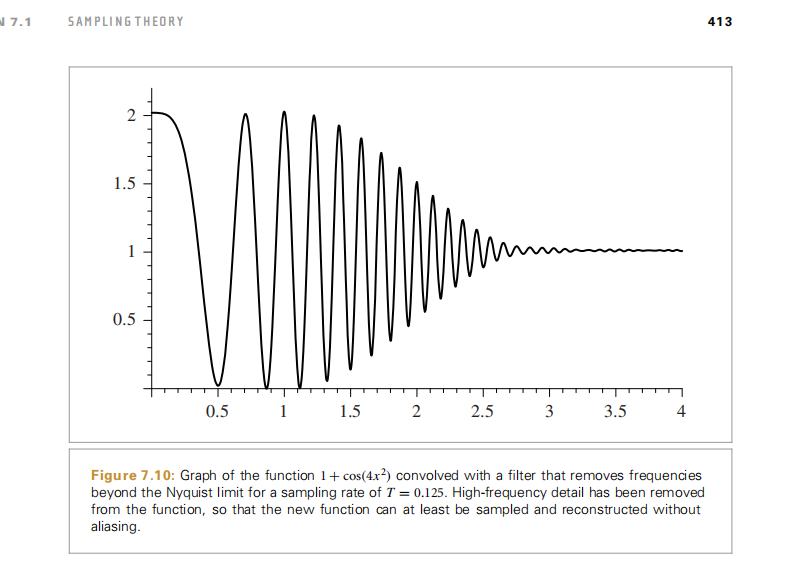
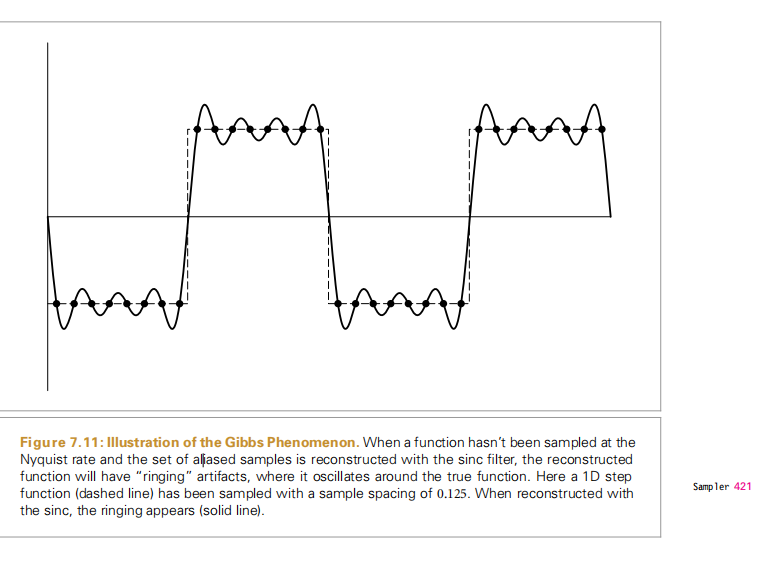
最后

以上就是顺心皮带为你收集整理的PBR来龙去脉十：低差异序列开头的全部内容，希望文章能够帮你解决PBR来龙去脉十：低差异序列开头所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。