SHAH FUNCTION

SHAH FUNCTION

Maths

Mathematically, Shah function is actually an extension of Delta function. This work will shed light on it in the context of its celebrated application --- Crystal Gazing --- for intuitive understanding.

Set-up

(1) X-rays were discovered in 1895 by Roentgen who concluded that they are waves with 10^-8 cm of wavelength, thus too small to measure;

(2) Crystals are atoms arrayed on a lattice. Max von Lave studied atomic crystal via diffraction approach with X-rays in 1912.

For experimental details, we need first bring up the fundamental hypothesis,

(1) X-rays are waves, so will diffract;

(2) Crystals have lattice atomic structure;

(3) Spacing of atoms is comparable to wavelength of X-rays.

Derivation                  

In one-dimensional case, we think of a 1-D crystal as evenly spaced along a line, effectively an infinite array, as shown Figure 1.

Figure 1

The function ro(x) denotes an electron density for a single atom. Then, the entire electron density distribution ro­_p(x) for crystal is given by the periodized version of ro(x),

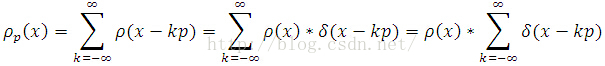
By defining

we have

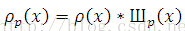
Figure 2 shows the pictorial representation of Shah_p(x), which is a periodization of Delta function.

Figure 2

In physics, a diffraction pattern is determined by the Fourier transform taken by nature. By taking the Fourier transform of ro_p(x), we obtain

where the Fourier transform of ro is a fixed function depending on the nature of crystal of interest. Question is, what is the Fourier transform of Shah_p(x)?

Taking p=1, we obtain a special case,

where Shah_p(x) makes senses as a distribution, which is defined by pairing with a test function in Schwartz class,

On the other hand,

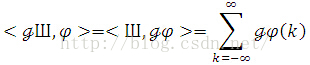
One can write down

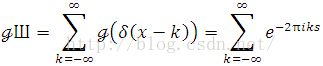
This doesn't converge classically. But it is fine as a distribution. However, we are missing something here.

To gain further progress, we have to introduce the deepest fact known about integers, the Poisson summation formula (See its proof in Appendix), given by

Therefore,

Consequently,

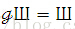
Back to the general case,

Therefore, by using the stretching property of Delta function, we represent Shah_p(x) in terms of Shah(x/p) with a coefficient of (1/p).

Further,

Consequently,

The process is illustrated in Figure 3.

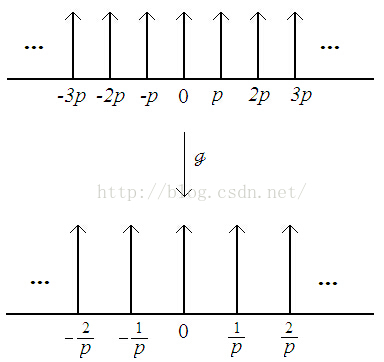
Figure 3

Armed with this technique, we can get back to crystal problem,

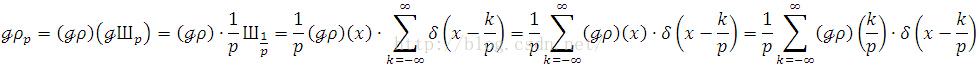
In conclusion, visually, you will see in a diffraction experiment a pattern spaced by (1/p). With nature taking a Fourier transform for you, you measure the spacing the pattern and reach a conclusion that the spacing length is the reciprocal of spacing in the atom in crystal.

Appendix I

Prove: for any rapidly decreasing function phi(x) and integers k,

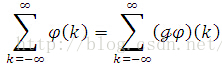
First, we periodize phi to have period of 1, i.e., (1)

Then, expand PHI in Fourier series,

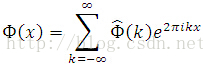
Knowing that the Fourier coefficient of the composed function by periodization equals the value evaluated at the Fourier transform of periodized function, i.e.,

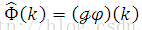
we have (2)

Finally, evaluating (1) and (2) at zero yields

Appendix II

According the derivation above, we obtain an important property,

最后

以上就是大胆酒窝为你收集整理的SHAH FUNCTION的全部内容，希望文章能够帮你解决SHAH FUNCTION所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。