【软考学习1】数据表示——进制转换，R进制转10进制 和 10进制转R进制

进制转换是软考必考的项目，首先对其进行复习。
进制转换模块可分为两块——R进制转10进制、10进制转R进制。

零、使用场景

日常生活中通常使用十进制，但计算机底层都是采用二进制计算，所以会涉及到进制转换。

一、十进制转R进制（短除法）

样例一

除法的计算公式为 被除数 ÷ 除数 = 商 + 余数。

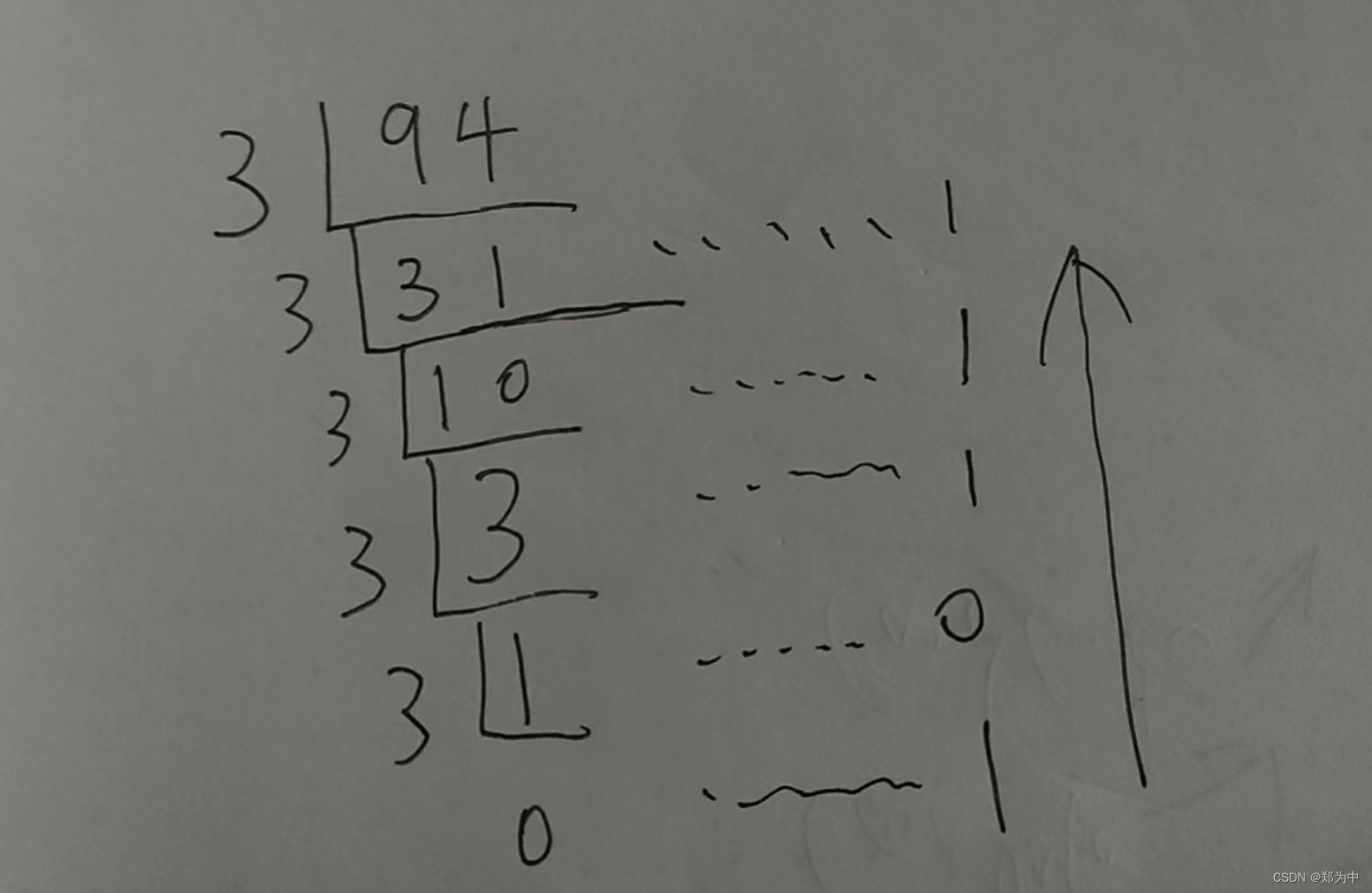
比如要将 94 转换为 3 进制，过程如下：

被除数 94 除以 3，商为 31，余数为 1；
被除数 31 除以 3，商为 10，余数为 1；
被除数 10 除以 3，商为 3，余数为 1；
被除数 3 除以 3，商为 1，余数为 0；
被除数 1 除以 3，商为 0，余数为 1；

所以从下到上，答案就是10111，如下图所示。

样例二

比如要将 68 转换为 6 进制，过程如下：

被除数 68 除以 6，商为 11，余数为 2；
被除数 11 除以 6，商为 1，余数为 5；
被除数 1 除以 6，商为 0，余数为 1；

所以从下到上，答案就是152，如下图所示。

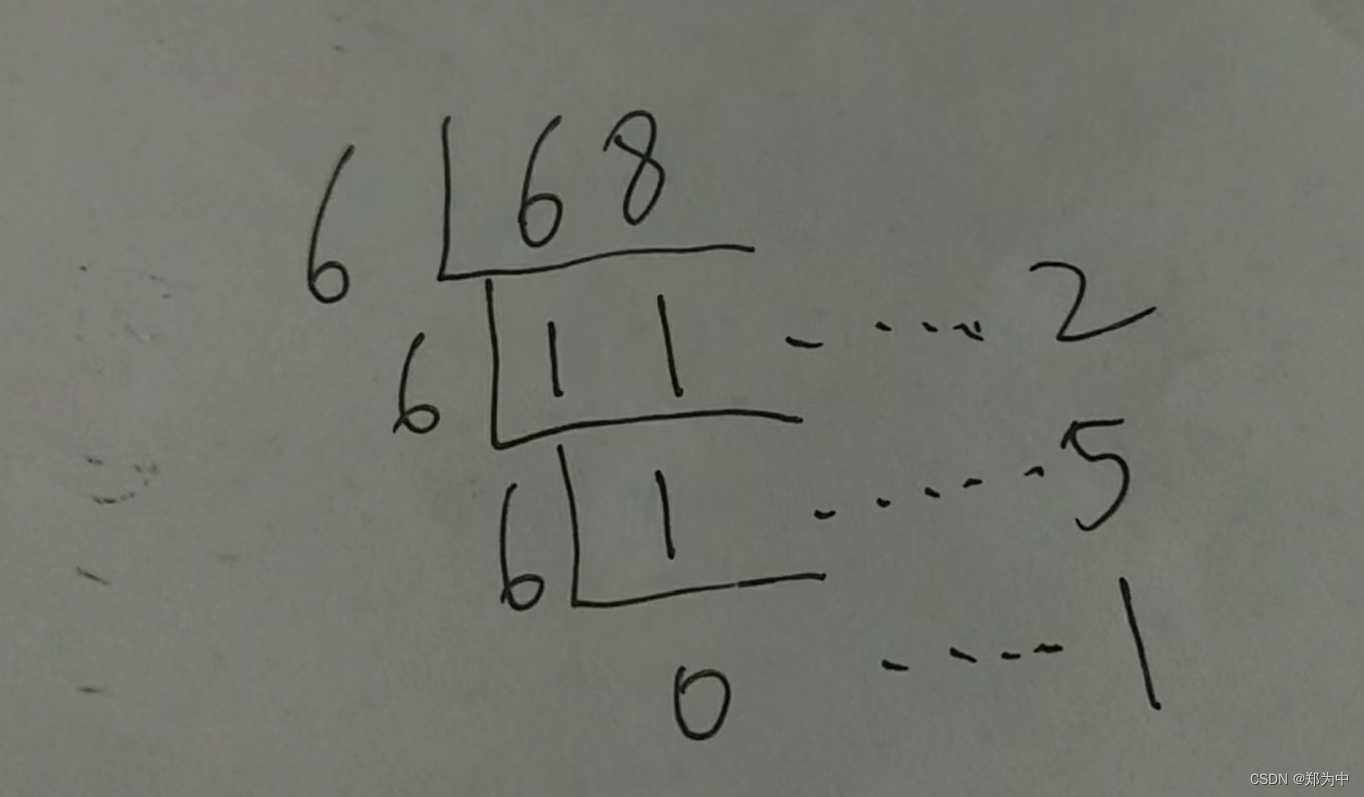
程序验证

结果可以采用 Java 程序验证，相关代码如下。

public static void main(String[] args) {
    // 转换前数字
    Integer number = 94;
    // 转换结果
    String ans = Integer.toString(number,3);
    // 94 转换为 3进制，答案为 10111
    System.out.println(ans);
}

二、R进制转十进制（按权展开法）

将 R 进制数的每一位拆为幂次方形式，幂的底数为 R，指数为 K，K 是数位和小数点的有向距离，左边为正，右边为负。

样例三

16进制数 6A8 转10 进制
第一位 6 ，拆分为 6 乘 16 的 2 次方。
第二位 A（即10），拆分为10 乘 16 的 1 次方。
第三位 8，拆分为 8 乘 16 的 0 次方。
再将所有结果相加，最终得到 1701 的答案，如下图所示。

样例四

比如13进制数 8B7 转10进制
第一位 8 ，拆分为 8 乘 13 的 2 次方。
第二位 B（即11），拆分为11 乘 13 的 1 次方。
第三位 7，拆分为 7 乘 13 的 0 次方。
再将所有结果相加，最终得到 1502 的答案，如下图所示。

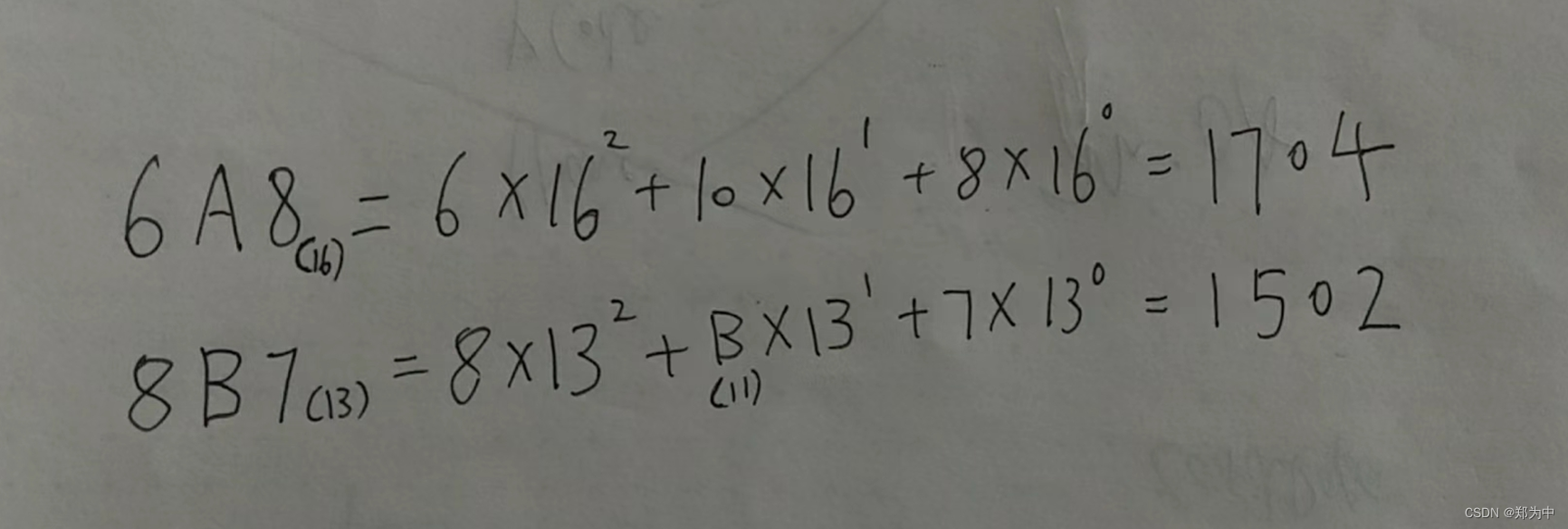
程序验证

结果可以采用 Java 程序验证，相关代码如下。

public static void main(String[] args) {
    String number = "8B7";
    Integer ans = Integer.parseInt(number,13);
    System.out.println(ans);
}

三、总结

今天对进制转换进行了学习，掌握了 R 进制转 10 进制 和 10进制转 R 进制的方法。

最后

以上就是无心可乐为你收集整理的【软考学习1】数据表示——进制转换，R进制转10进制 和 10进制转R进制的全部内容，希望文章能够帮你解决【软考学习1】数据表示——进制转换，R进制转10进制 和 10进制转R进制所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。