一【题目难度】

• 乙级

二【题目编号】

• 1049 数列的片段和 (20 分)

三【题目描述】

• 给定一个正数数列，我们可以从中截取任意的连续的几个数，称为片段。例如，给定数列 { 0.1, 0.2, 0.3, 0.4 }，我们有 (0.1) (0.1, 0.2) (0.1, 0.2, 0.3) (0.1, 0.2, 0.3, 0.4) (0.2) (0.2, 0.3) (0.2, 0.3, 0.4) (0.3) (0.3, 0.4) (0.4) 这 10 个片段。
• 给定正整数数列，求出全部片段包含的所有的数之和。如本例中 10 个片段总和是 0.1 + 0.3 + 0.6 + 1.0 + 0.2 + 0.5 + 0.9 + 0.3 + 0.7 + 0.4 = 5.0。

四【题目示例】

• 输入格式：
  输入第一行给出一个不超过 $10^5$ 的正整数 $N$，表示数列中数的个数，第二行给出 $N$ 个不超过 1.0 的正数，是数列中的数，其间以空格分隔。

• 输出格式：
  在一行中输出该序列所有片段包含的数之和，精确到小数点后 2 位。

• 输入样例：
  4
  0.1 0.2 0.3 0.4

• 输出样例：
  5.00

五【解题思路】

• 这个题是真的没想到啊，确实是一个数学问题，更确切的说是找规律：如果当前是第$i$个数，那么其总出现次数等于$i\ast (n+1-i)$次，所以只需要遍历每一个数字，累加起来就行，要是还不懂，可以看下面的图就明白了（此图来自算法笔记-上机训练实战指南-胡凡），其中还需要注意：使用double类型会有一个测试用例不能通过，有可能是数字太大，计算机中以二进制存储时会损失精度（学过计算机组成原理可能更好理解），所以每次将临时结果转换为$longlong$类型，记得要乘1000之后再转，这样不会损失精度，输出结果的时候再除以1000.0，注意不能除以1000，否则又会损失精度
  

六【最终得分】

• 20分

七【代码实现】

#include<stdio.h>
int main()
{
    int n;
    scanf("%d",&n);
    double temp;
    long long res = 0.0;
    for(int i = 1;i<=n;i++)
    {
        scanf("%lf",&temp);
        res += (long long)(temp * 1000) * i * (n + 1 - i);
    }
    printf("%.2lf",res / 1000.0);
    return 0;
}

八【提交结果】

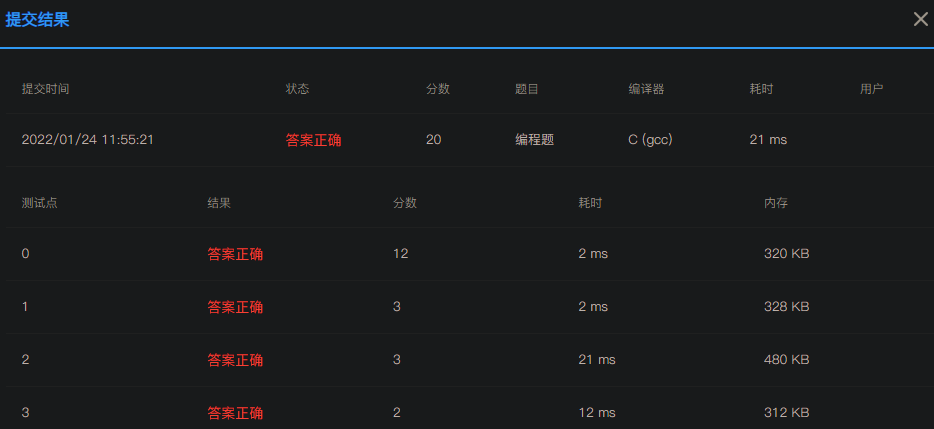
最后

以上就是灵巧超短裙为你收集整理的【PAT (Basic Level) Practice】——【简单数学】1049 数列的片段和一【题目难度】二【题目编号】三【题目描述】四【题目示例】五【解题思路】六【最终得分】七【代码实现】八【提交结果】的全部内容，希望文章能够帮你解决【PAT (Basic Level) Practice】——【简单数学】1049 数列的片段和一【题目难度】二【题目编号】三【题目描述】四【题目示例】五【解题思路】六【最终得分】七【代码实现】八【提交结果】所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。