从多重背包到混合背包

83 阅读 0 评论 55 点赞

我是靠谱客的博主微笑铅笔，最近开发中收集的这篇文章主要介绍从多重背包到混合背包，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

多重背包

在这里插入图片描述
所谓多重背包就是每种物品有数量限制，一个很自然的想法就是把01背包的状态方程稍微修改一下，每种物品有0、1、2…p[i]件选法，多一重枚举即可。

f[i][j] = max(f[i-1][j], f[i-1][j-k*w[i]] + k * v[i]) (k:0->p[i])

这也就是将p[i]分解，但是我们为什么不采取一种更有效率的分解方法？你看任何数都可以按照二进制位进行分解，举个栗子，比如15(10)就是1111(2)，那么1~15的任何数字都可以通过8、4、2、1组成。

为什么是01背包的加强版呢？因为我将数量为13的这种物品分解成1、2、4、6这几种数量之后相当于分别变成了重量分别为1w、2w、4w、6w这四种不同重量但数量为1的物品（w为一件物品的重量）

那么问题来了，怎么分解呢？

for (int i = 1; i <= n; i++) {
    int num = min(p[i], V / w[i]);//如果装不下，你有再多也是白搭
    for (int k = 1; num > 0; k <<= 1) {
        if (k > num) k = num;//1 2 4 后面不是8，而是6（总共有13件时）
        num -= k;
        for (int j = V; j >= w[i] * k; j--)
            f[j] = max(f[j], f[j - w[i] * k] + v[i] * k);
    }
}

模板题背过

①Dividing
这题我老老实实套上面的模板然后TLE了，哭晕！拆，就硬拆！把好多重背包按照上述二进制方法拆分成若干个小物件然后01背包！我还不信了，这还不过！
有亿点点????坑！WA了几发，TLE了几发，大家加油????

#include <bits/stdc++.h>
using namespace std;

const int N = 20010;

int marbles[7];
bool flag = true;
int sum, cnt;
int f[N], divide[N];

void p(int x, bool f){
	printf("Collection #%d:n", x);
	if(f) printf("Can be divided.n");
	else printf("Can't be divided.n");
}

void solve(){
	while(flag){
		cnt++, sum = 0; 
		if(cnt!=1) printf("n");
		for (int i = 1; i <= 6; ++i)
		{
			scanf("%d", &marbles[i]);
			sum += marbles[i] * i;
		}
		if(sum == 0) {flag = false; break;}
		if(sum % 2 == 1){p(cnt, false);continue;}
		sum /= 2;
		int l = 0;
		memset(divide, 0, sizeof divide);
		memset(f, 0, sizeof f);
		for (int i = 1; i <= 6; ++i)
		{
			for (int j = 1; j <= marbles[i]; j <<= 1)
			{
				divide[l++] = j * i;//价值就是i，注意divide数组的下标是l++
				marbles[i]-= j;//记得更新数量
			}
			if(marbles[i] > 0) divide[l++] = marbles[i] * i;//注意处理剩下的
		}
		for (int i = 0; i < l; ++i)//物品数量更新到了l，而且是从0开始的
		{
			for (int j = sum; j >= divide[i]; j--)
			{
				f[j] = max(f[j], f[j - divide[i]] + divide[i]);
			}
		}
		if(f[sum] == sum) p(cnt, true);
		else p(cnt, false);
	}
}

int main(int argc, char const *argv[])
{
	solve();
	return 0;
}

②P1776 宝物筛选
这题我没有像上面那样硬拆也没超时hhh，那就酱~

#include <bits/stdc++.h>
using namespace std;

const int N = 4e4 + 10;

struct treasure
{
	int v, w, m;//价值，重量，件数
}t[105];

int n, W;
int f[N];

void solve(){
	scanf("%d%d", &n, &W);
	for (int i = 1; i <= n; ++i)
		scanf("%d%d%d", &t[i].v, &t[i].w, &t[i].m);
	for (int i = 1; i <= n; ++i)
	{
		int num = min(t[i].m, W / t[i].w);
		for (int k = 1; num > 0; k <<= 1)
		{
			if(k > num) k = num;
			num -= k;
			for (int j = W; j >= t[i].w * k; --j)
			{
				f[j] = max(f[j], f[j - t[i].w * k] + t[i].v * k);
			}
		}
	}
	printf("%dn", f[W]);
}

int main(int argc, char const *argv[])
{
	solve();
	return 0;
}

混合背包

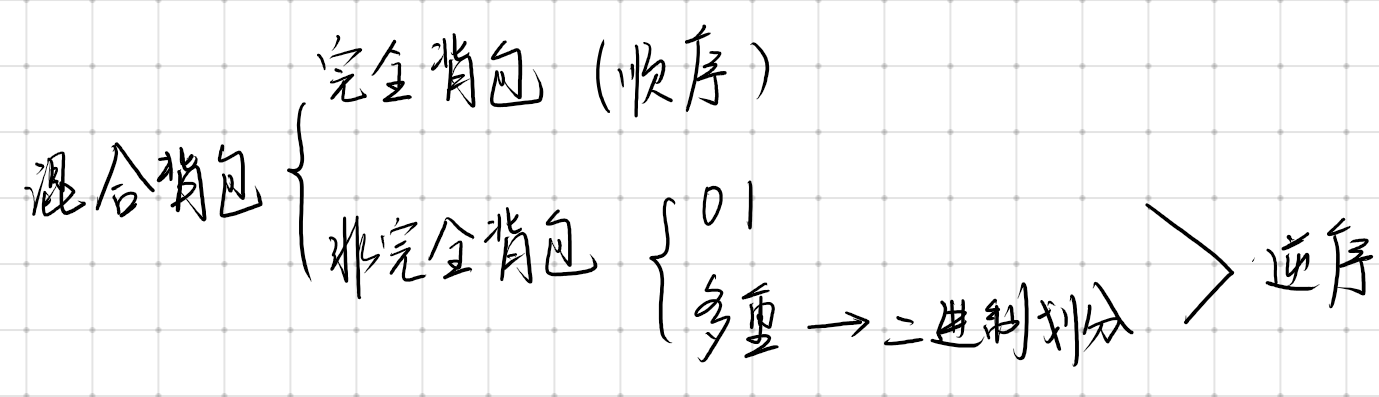
什么叫混合背包呢？顾名思义，混合就是既有A又有B，还有C，A就是01背包，B就是完全背包，C就是多重背包。
在这里插入图片描述
这也太会了吧！但是你以为这样就是究极版本吗？大错特错了，这还只是把前面的知识融会贯通一遍，后面还有更精彩的呢！
聪明如你，一定可以想到这几种情况的混合也不过是按照情况的不同分类处理——
在这里插入图片描述

//p[i]:每个物品的件数，0代表无穷个
for (int i = 1; i <= n; i++)
    if (p[i] == 0)
        for (int j = w[i]; j <= V; j++)
            f[j] = max(f[j], f[j - w[i]] + v[i]);
    else
    for (int k = 1; k <= p[i]; k++)
        for (int j = V; j >= w[i]; j--)
            f[j] = max(f[j], f[j - w[i]] + v[i]);

模板题背过

①P1833 樱花

#include <bits/stdc++.h>
using namespace std;

const int N = 1e3 + 10;
const int M = 1e4 + 10;

int f[N];
struct Tree
{
	int T, C, P;//体积，价值，个数
}t[M];
int n, V;//件数，容积

void solve(){
	int h1, m1, h2, m2;
	scanf("%d:%d %d:%d", &h1, &m1, &h2, &m2);//注意数据的读入方式
	V = (h2 - h1) * 60 + (m2 - m1);
	scanf("%d", &n);
	for (int i = 1; i <= n; ++i)
		scanf("%d%d%d", &t[i].T, &t[i].C, &t[i].P);
	for (int i = 1; i <= n; ++i)
	{
		if(t[i].P == 0){//无限次
			for (int j = t[i].T; j <= V; ++j)//从前往后
				f[j] = max(f[j], f[j - t[i].T] + t[i].C);
		}else{
			int num = min(t[i].P, V / t[i].T);
			for (int k = 1; num > 0; k <<= 1)
			{
				if(num < k) k = num;
				num -= k;
				for (int j = V; j >= k * t[i].T; j--)//从后往前
				{
					f[j] = max(f[j], f[j - k * t[i].T] + k * t[i].C);
				}
			}
		}
	}
	printf("%dn", f[V]);
}

int main(int argc, char const *argv[])
{
	solve();
	return 0;
}