题目

思路
本题极其类似于最优矩阵链乘,同样是最优子结构,同样是二分区间DP,唯一的不同在于本题难以简洁地表达子问题。
为什么呢?类似于最优矩阵链乘。
A1A2A3A4A5A6
A
1
A
2
A
3
A
4
A
5
A
6
—- >>>>
(A1A2)(A3A4A5A6)
(
A
1
A
2
)
(
A
3
A
4
A
5
A
6
)
(1,6)−−−−>>>>(1,2)(3,6)
(
1
,
6
)
−
−
−
−
>>>>
(
1
,
2
)
(
3
,
6
)
不管怎么分,子问题都可以简洁地用一个区间来表达。
但是三角剖分,你剖分的这一刀可以是在任意的两个点,这就造成了在如下情况:
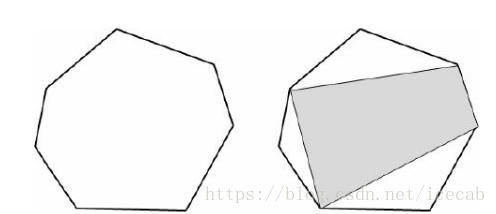
就很难用一个区间就能表示的了。
因此有必要把决策的顺序规范化,使得在规范的决策顺序下,任意状态都能用区间表示。
1.状态定义:d(i,j),由点表示的子多边形i,i+1,…,j-1,j的最优值。
2.边界:d(i,i+1)=0
3.答案:d(1,n)
4.状态转移方程:
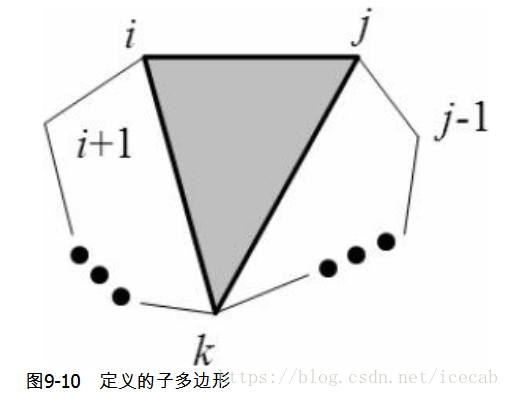
5.复杂度: O(n3) O ( n 3 )
代码
没有任何OJ上有本题的模板题,也没有找到任何的样例数据。。。所以只能凭感觉反映一下思路即可,下面的代码有99%的可能性有bug
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <cmath>
#include <algorithm>
#define _for(i,a,b) for(int i = (a); i<(b); i++)
#define _rep(i,a,b) for(int i = (a); i<=(b); i++)
using namespace std;
const int maxn = 100 + 10;
int n, w[maxn][maxn][maxn], d[maxn][maxn];
int main() {
scanf("%d", &n);
// 三角形权值可以是周长,面积等,此处假设题目输入
_rep(i, 1, n)
_rep(j, 1, n)
_rep(k, 1, n)
scanf("%d", &w[i][j][k]);
_rep(i, 1, n - 1) d[i][i + 1] = 0;
int j;
_rep(l,2,n)
_rep(i, 1, n) {
j = i + l;
if (j > n) continue;
_rep(k, i + 1, j - 1)
d[i][j] = max(d[i][j], d[i][k] + d[k][j] + w[i][j][k]);
}
printf("%dn", d[1][n]);
return 0;
}最后
以上就是和谐茉莉最近收集整理的关于[区间DP] 凸边形三角剖分(子问题的表达)的全部内容,更多相关[区间DP]内容请搜索靠谱客的其他文章。




![[区间DP] 凸边形三角剖分(子问题的表达)](https://www.shuijiaxian.com/files_image/reation/bcimg7.png)



发表评论 取消回复