【33. 0 1 背包问题】

背包问题

• 一共有N件物品，背包容量为V,物品有俩个属性，一个是体积一个是价值（类似在一个宝岛上，你有一个背包，它只能装满这个背包，小岛上有很多金子，各种体积的，而且每个金子纯度不一样，看最后怎么装才会使得背包中的金子价值最高）

四种背包问题

• 0 1 背包 每件物品最多只用一次，
• 完全背包 每件物品有无线个
• 多重背包 每个物品不一样，每个物品最多有有S_i个——朴素版和优化版
• 分组背包 有水果，汽车，人等，每一种里面最多只能选择一个

思路：

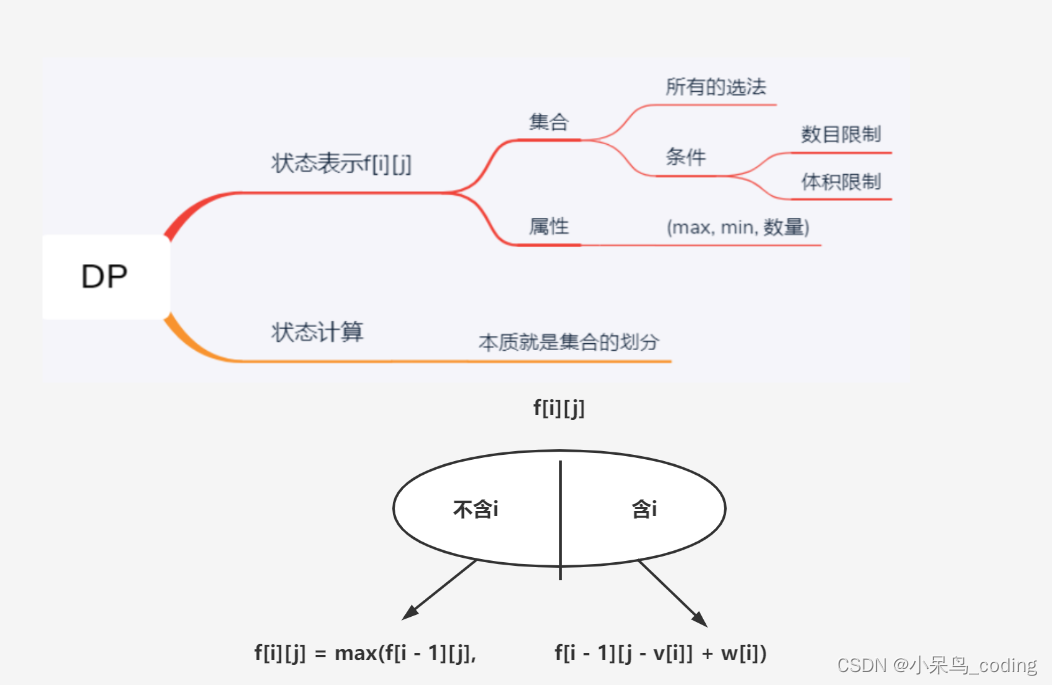
注意

• 在f[i][j]划分集合时，左边的情况是一定存在的，但是右边的情况不一定存在（当容量j < v[i]时，也就是最后一个物品的体积，大于总容量时。）

集合如何划分

• 一般原则:不重不漏,不重不一定都要满足(一般求个数时要满足)

• 如何将现有的集合划分为更小的子集,使得所有子集都可以计算出来.

方法1：二维dp

（1）转态f[i][j]: 前 i 个物品，背包容量 j 下的最优解（最大价值）

• 当前的状态依赖于之前的状态，可以理解为从初始状态f[0][0] = 0,开始决策，有 N 件物品，则需要 N 次决 策，每一次对第 i 件物品的决策,状态f[i][j]不断由之前的状态更新而来

（2）当前背包容量不够（j < v[i]），没得选，因此前 i 个物品最优解等于前 i−1 个物品最优解：

• 对应代码：f[i][j] = f[i - 1][j]

(3) 当前背包容量够，可以选，因此需要决策选与不选第 i 个物品：

• 选：f[i][j] = f[i - 1][j - v[i]] + w[i]。
• 不选：f[i][j] = f[i - 1][j] 。
• 我们的决策是如何取到最大价值，因此以上两种情况取 max() 。

注意：

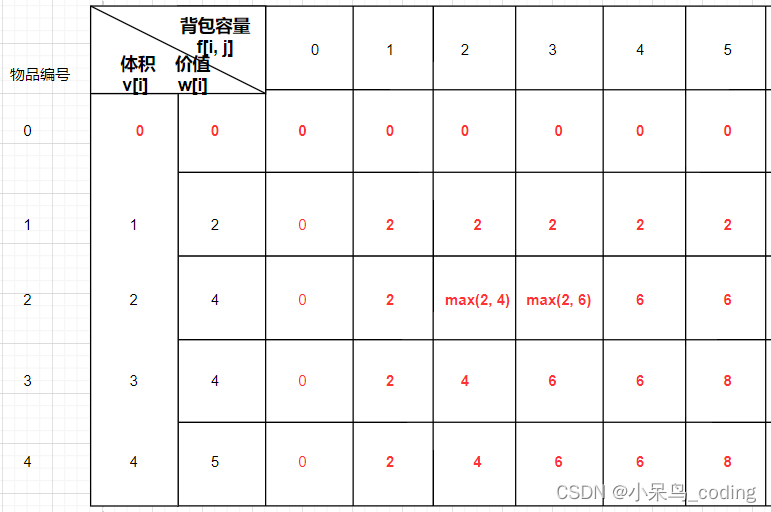
• 当进行初始化的时候，需要枚举所有的状态f[0~n][0~m]
• 对于f[0][0~m]来说值始终为0，因为0代表没有物品(0件物品，总体积不超过0,1,2，...m)的最大价值是多少
• f[i-1][j]:不选第i个物品的集合中的最大值
• f[i-1][j-v[i]]+w[i]:选第i个物品的集合,但是直接求不容易求所在集合的属性,于是先将第i个物品的体积减去,求剩下集合中选法的最大值.然后再加上第i个物品的价值
  

题目

代码

#include <iostream>
#include <algorithm>
using namespace std;

const int N = 1010;
int n, m;             //n为物品个数，m为物品容量
int f[N][N];          //定义了全局变量，默认就是0。
int v[N],w[N]; 

int main()
{
    cin >> n >> m;
    for (int i = 1; i <= n; i ++)  cin >> v[i] >> w[i];
    
    for (int i = 1; i <= n; i ++)
    {
        for (int j = 0; j <= m; j ++)
        {
            f[i][j] = f[i - 1][j];
            if (j >= v[i]) f[i][j] = max(f[i][j], f[i - 1][j - v[i]] + w[i]);
        }
    }
    
    cout << f[n][m] << endl;
    return 0;
}

方法2：一维dp

f[i]这一层只用到了f[ i - 1]这一层，而f[i - 2]到f[0]这些层都没有用到，所以可以用滚动数组来做
将状态f[i][j]优化到一维f[j]，实际上只需要做一个等价变形。

为什么可以这样变形呢？我们定义的状态f[i][j]可以求得任意合法的i与j最优解，但题目只需要求得最终状态f[n][m]，因此我们只需要一维的空间来更新状态。

• （1）状态f[j]定义：N 件物品，背包容量j下的最优解。
• （2）注意枚举背包容量j必须从m开始。
• （3）为什么一维情况下枚举背包容量需要逆序？在二维情况下，状态f[i][j]是由上一轮i - 1的状态得来的，f[i][j]与f[i - 1][j]是独立的。而优化到一维后，如果我们还是正序，则有f[较小体积]更新到f[较大体积]，则有可能本应该用第i-1轮的状态却用的是第i轮的状态。
• （4）简单来说，一维情况正序更新状态f[j]需要用到前面计算的状态已经被「污染」，逆序则不会有这样的问题。

正序
f[1] = max(f[1], f[0] + w[1])
f[2] = max(f[2], f[2 - v[1]] + w[1]) = max(f[2], f[1] + w[1])
f[3] = max(f[3], f[3 - v[1]] + w[1]) = max(f[3], f[2] + w[1])

• 发现中间f[2]已经是计算出来的，已经更改了，被污染的，然后将这个已经更改的f[2]又传给了下面，这是错误的

逆序
f[4] = max(f[4], f[4 - v[1]] + w[1]) = max(f[4], f[3] + w[1])
f[3] = max(f[3], f[3 - v[1]] + w[1]) = max(f[3], f[2] + w[1])
f[2] = max(f[2], f[2 - v[1]] + w[1]) = max(f[2], f[1] + w[1])

总结：

• j-v[i]<=j,j是递增更新的，所以f[j-v[i]]是第i层计算过了，就是相当于，我用一个已经更新的值，又进行计算了
• 如果直接把f[i]删掉的话，直接等价于f[i][j] = max(f[i][j], f[i ][j - v[i]] + w[i]),而正确是f[i][j] = max(f[i][j], f[i - 1][j - v[i]] + w[i]),所以需要倒序
• 如果是正序枚举，因为j-v[i] < j,肯定会比f[j]早更新到（从第i-1层转移到了第i层），因为此时的f[j-v[i]]不是我们想要的第I-1层的状态，而是第i层的

代码

#include <iostream>
using namespace std;

const int N = 1010;
int n, m;
int f[N], v[N], w[N];

int main()
{
    cin >> n >> m;
    for (int i = 1; i <= n; i ++)  cin >> v[i] >> w[i];
    for (int i = 1; i <= n; i ++)
    {
        for (int j = m; j >= v[i]; j --)
        {
        
             f[j] = max(f[j], f[j - v[i]] + w[i]);
        }
    }
    cout << f[m];
    return 0;
}

最后

以上就是直率导师为你收集整理的【33. 0 1 背包问题】的全部内容，希望文章能够帮你解决【33. 0 1 背包问题】所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。