【c++回顾】3.1经典算法问题-完全背包问题2--背包价值最大问题

接上一篇博客，继续解决完全背包问题。
问题描述：给定n种物品和一个背包。物品i的重量是wi，其价值为vi，背包的容量为C。应该如何选择装入背包中的物品，使得装入背包中物品的总价值最大？每种物品有无限个。
利用上一篇博客的子功能，我们可以获得所有的使背包饱和（即无法再装入任何一个物品）的方案，求取所有方案的背包价值，找出最大价值及其对应的拿取方案即可。
上代码：

//给定n种物品和一个背包。物品i的重量是wi，其价值为vi，背包的容量为C。应该如何选择装入背包中的物品，使得装入背包中物品的总价值最大？每种物品有无限个
//利用完全背包填满问题的递归函数，遍历得到所有使背包饱和的结果，求取每个方案的价值，查找最大值并输出最佳拿取方案

#include "pch.h"
#include <iostream>
#include <vector>
#include <math.h>
using namespace std;

//打印拿取方案
void PrintVector(vector<int> take_or_not)
{
	cout << "【最佳拿取方案】" << endl;
	for (int i = 0; i < take_or_not.size(); i++)
	{
		cout << "拿取" << "第" << i << "个物品:" << take_or_not[i] << " 个" << endl;
	}
	cout << endl;
}
//给出拿取情况向量与重量列表向量，求解当前背包重量,也可以用于求解价值
int CalculateWeight(vector<int> taken_items, vector<int> weights)
{
	int weight = 0;
	for (int i = 0; i < taken_items.size(); i++)
		weight = weight + taken_items[i] * weights[i];
	return weight;
}
//判断剩余空间能否放下从i开始的某个物品，一个都放不了则返回False
bool TakeMore(vector<int> weights, int left_capacity, int i)
{
	for (; i < weights.size(); i++)
	{
		if (weights[i] <= left_capacity)
			return true;
	}
	return false;
}
/*递归解决该问题*/
//给出背包（剩余）容量，物品重量列表，拿取方案列表，要拿取的物品位置i
//主函数调用时先初始化take_or_not与i为0
//该问题中，solutions用于存储所有使背包饱和的拿取方案
void Recursion(int capacity, vector<int> weights, vector<int>& take_or_not, int i, vector<vector<int>>& solutions)
{
	int left_capacity = capacity - CalculateWeight(take_or_not, weights);
	//如果已经到最后一个物品，则直接用最后一个物品装满背包，进行操作，并返回
	if (i == (take_or_not.size() - 1))
	{
		take_or_not[i] = left_capacity / weights[i];
		//更新left_capacity
		left_capacity = capacity - CalculateWeight(take_or_not, weights);
		if (take_or_not[i] >= 0)
		{
			//判断当前拿取方案是否饱和，如果每个物品都放不下了再进行操作
			if (!TakeMore(weights, left_capacity, 0))
			{
				//operation,存储当前拿取方案
				solutions.push_back(take_or_not);
			}
		}
		//返回前将最后一个物品清空
		take_or_not[i] = 0;
		return;
	}
	//定义flag，用于判断是否执行了for循环
	bool flag = false;
	//第i个物品数量从0开始递增，直到装满背包为止，每加1就对i+1进行递归
	for (int o = 0; weights[i] <= left_capacity; o++)
	{
		take_or_not[i] = o;
		//更新left_capacity
		left_capacity = capacity - CalculateWeight(take_or_not, weights);
		Recursion(capacity, weights, take_or_not, i + 1, solutions);
		flag = true;
	}
	//如果当前i不是最后一个物品,且未执行for循环，则继续递归
	if (i != take_or_not.size() - 1 && !flag)
		Recursion(capacity, weights, take_or_not, i + 1, solutions);
	//当前物品遍历结束后，该物品数量清零并返回
	take_or_not[i] = 0;
	return;
}
//在solution中查找并输出背包价值最大值及最佳拿取方案
void Backpack(vector<vector<int>> solutions, vector<int> values)
{
	//定义最大价值，初始化为0
	int max_value = 0;
	//第一次遍历，求得最大值，并输出
	for (auto solution : solutions)
	{
		int current_value = CalculateWeight(solution, values);
		max_value = max_value > current_value ? max_value : current_value;
	}
	cout << "【背包最大价值】" << endl << max_value << endl;
	//第二次遍历，求得最佳拿取方案，并输出
	for (auto solution : solutions)
	{
		int current_value = CalculateWeight(solution, values);
		if (current_value == max_value)
			PrintVector(solution);
	}
}

int main()
{
	//初始化
	int capacity;
	vector<int> weights;
	vector<int> values;
	int number;
	cout << "输入背包容量及物品件数：" << endl;
	cin >> capacity >> number;
	cout << "输入这" << number << "个物品的重量" << endl;
	for (int i = 0; i < number; i++)
	{
		int weight;
		cin >> weight;
		weights.push_back(weight);
	}
	cout << "输入这" << number << "个物品的价值" << endl;
	for (int i = 0; i < number; i++)
	{
		int value;
		cin >> value;
		values.push_back(value);
	}
	//定义拿取方案，用于递归
	vector<int> take_or_not(number, 0);
	//定义递归操作符
	int i = 0;
	//定义solutions，用于存储所有使背包饱和的拿取方案
	vector<vector<int>> solutions;
	//递归获取所有solution
	Recursion(capacity, weights, take_or_not, i, solutions);
	//在solution中查找并输出背包价值最大值及最佳拿取方案
	Backpack(solutions, values);

	return 0;
}
/*
输入：
10 3
2 5 8
1 4 7
*/

示例运行结果：

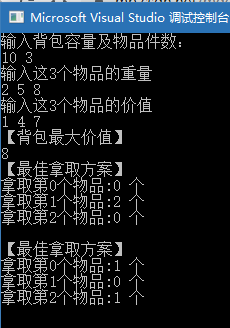
最后

以上就是沉静宝马为你收集整理的【c++回顾】3.1经典算法问题-完全背包问题2--背包价值最大问题的全部内容，希望文章能够帮你解决【c++回顾】3.1经典算法问题-完全背包问题2--背包价值最大问题所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。