完全背包问题：最大价值(java)

81 阅读 0 评论 54 点赞

我是靠谱客的博主高高秋天，最近开发中收集的这篇文章主要介绍完全背包问题：最大价值(java)，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

题目来源
在这里插入图片描述
完全背包问题是每件物品可以使用无限次，而01背包问题是每件物品最多可以使用一次(用或者不用两种情况)

示例
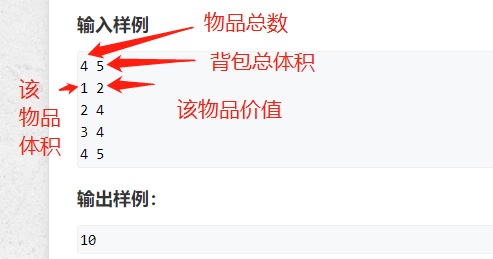
在这里插入图片描述
分析
要求的是放哪些物品，分别放多少件，使总价值最大

for(int i = 1;i <=物品总数;i++){
//物品总数做最外层循环，那么物品放进背包是有顺序的。
//如果一种结果是(物品1，物品2)，那只有一种情况，
//而不会出现(物品1，物品2)和(物品2，物品1)两种情况
//虽然在这里没有影响，但是如果问题是求方案数的时候，则会出问题
	for(int j = v[i];j <= 背包总容量;j++){
	//因为j<v[i]时，该物品不会被选，所以从v[i]开始遍历，可以减少循环次数
		for(int k = 0;k*v[i]<=j;k++){
		//每种物品，遍历从不放入到最多可放入k件，计算总价值
			dp[i][j] = Math.max(dp[i-1][j],dp[i-1][j-k*v[i]]+k*w[i]);
		}
	}
}
dp[i][j]=max(dp[i-1][j],dp[i-1][j-v[i]]+w[i],...,dp[i-1][j-k*v[i]]+k*w[i]);
dp[i][j-v[i]] = max(dp[i-1][j-v[i]],...,dp[j-1][j-k*v[i]]+(k-1)*w[i])
=>dp[i][j] = max(dp[i-1][j],dp[i][j-v[i]]+w[i])
对j从小到大遍历
对于第i层循环，遍历到dp[i][j]时，dp[i][j-v[i]]也一定遍历到了,但dp[i][j]用的是dp[i-1][j]的值
所以有
dp[j] = max(dp[j],dp[j-v[i]]+w[i]) 等价于 dp[i][j] = max(dp[i-1][j],dp[i][j-v[i]]+w[i])

具体代码

import java.util.Scanner;

public class Main{
    public static void main(String[] args){
        Scanner sc = new Scanner(System.in);
        int m = sc.nextInt();
        int n = sc.nextInt();
        int[] v = new int[m+1];
        int[] w = new int[m+1];
        int[] dp = new int[n+1];
        for(int i = 1;i <= m;i++){
            v[i] = sc.nextInt();
            w[i] = sc.nextInt();
        }
        for(int i = 1;i <= m;i++){
            for(int j =v[i]; j <= n;j++){
                dp[j] = dp[j];
                if(j >= v[i]){
                    dp[j] = Math.max(dp[j],dp[j-v[i]]+w[i]);
                }
            }
        }
        System.out.println(dp[n]);
    }
}