背包问题之3

设有一个背包可以放入的物品重量为S，现有n件物品，重量分别为w1，w2，w3，……，wn。问：能否从这n件物品中选择若干件放入次背包，使得放入的重量之和正好为S。如果存在一种符合上述要求的选择，则称此背包问题有解（或称解为“真”），否则此问题无解（或解为“假”）。

算法设计：递归枚举
背包问题3与背包问题1,2的根本差别在于：背包问题1所选的物品件数是固定的常量，备选物品件数可以是可知的变量；背包问题2备选物品件数是固定常量且较小，所选物品件数不定；而背包问题3备选物品件数是可知的变量，所选物品件数也是不定的。因此背包问题3没有可以用固定的（常量个）嵌套循环来枚举的对象。这种情况可以用递归算法来解决。
C++代码：

    #include <iostream>
#include <vector>
using namespace std;

//如果能在sz件物品中选择若干件物品放入背包，使背包的重量正好为w，则返回true，否则返回false
bool fun(int w, vector<int> &v, int sz)
{
    if (w == 0)
    {
        return true;
    }
    else if (w < 0)
    {
        return false;
    }
    else
    {
        if (sz <= 0)
        {
            return false;
        }
        /*return fun(w-v[sz-1], v, sz-1) || fun(w, v, sz-1);*/
        if ( fun(w-v[sz-1], v, sz-1) )
        {
            cout<<"选择"<<v[sz-1]<<'t';
            return true;
        }
        else
            return fun(w, v, sz-1);
    }
}

int main()
{
    cout<<"请输入背包可以放入物品的总重量：";
    int w;
    cin>>w;
    vector<int> v;
    int t;
    cout<<"请分别输入物品的重量：";
    while (cin>>t)
    {
        v.push_back(t);
    }
    int sz = v.size();
    if(fun(w,v,sz))
    {
        cout<<"有解"<<endl;
    }
    else
    {
        cout<<"无解"<<endl;
    }
    return 0;
}

运行结果：

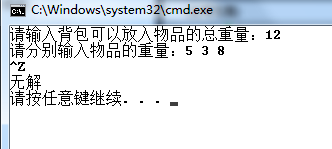
最后

以上就是动听小鸽子为你收集整理的背包问题之3的全部内容，希望文章能够帮你解决背包问题之3所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。