1. 首页
  2. 文章中心
  3. C语言

数字图像处理笔记(八)彩色图像和彩色图像直方图均衡化 1. 彩色空间 2. HSI空间进行直方图均衡化 3. 代码 4. 参考文献

80 阅读 0 评论
我是靠谱客的博主 坚定小虾米，最近开发中收集的这篇文章主要介绍数字图像处理笔记(八)彩色图像和彩色图像直方图均衡化 1. 彩色空间 2. HSI空间进行直方图均衡化 3. 代码 4. 参考文献 ，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

0. 前言

  今天是10.24节，假装在考研过程中百忙中给自己放一个假，好吧只是骗自己的，继续写笔记罢了，读了好多文章和冈萨雷斯老师的书感觉彩色图像处理这一块都不是讲的很细，可能是理论太过于繁琐而实践的时候都已经有封装好的API了吧

1. 彩色空间

1.1 RGB空间

  这个是应该是人人都认识的色彩空间了，
在 RGB 模型中，每种颜色出现在红、绿、蓝的颜色光谱分量中。该模型基于笛卡儿坐标系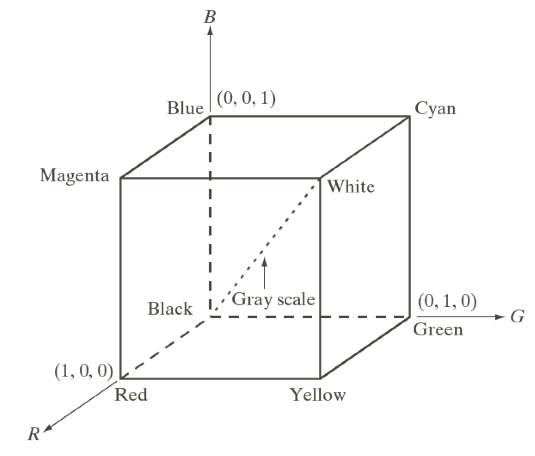在这里插入图片描述
只不过在实际处理的时候我们都是灰度图合并起来罢了，一般都是三个分量即R、G、B分量，8bit图像值在0-255之间。
  事实上，在我们遥感传统所见到的真彩色图像也是种假彩色图像，它是R、G、B图像按照一定的比例混合起来合成一幅灰度图，而只不过这幅灰度图和人眼感受到的真实世界很像，所以我们称其为真彩色图像罢了。
即：

     D
    
    
     N
    
    
     =
    
    
     0.2989
    
    
     ∗
    
    
     R
    
    
     +
    
    
     0.5870
    
    
     ∗
    
    
     G
    
    
     +
    
    
     0.1140
    
    
     ∗
    
    
     B
    
   
   
    DN = 0.2989 ∗ R + 0.5870 ∗ G + 0.1140 ∗ B
   
  
 </span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.68333em; vertical-align: 0em;"></span><span class="mord mathdefault" style="margin-right: 0.02778em;">D</span><span class="mord mathdefault" style="margin-right: 0.10903em;">N</span><span class="mspace" style="margin-right: 0.2777777777777778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right: 0.2777777777777778em;"></span></span><span class="base"><span class="strut" style="height: 0.76666em; vertical-align: -0.08333em;"></span><span class="mord">0</span><span class="mord">.</span><span class="mord">2</span><span class="mord">9</span><span class="mord">8</span><span class="mord">9</span><span class="mord">∗</span><span class="mord mathdefault" style="margin-right: 0.00773em;">R</span><span class="mspace" style="margin-right: 0.2222222222222222em;"></span><span class="mbin">+</span><span class="mspace" style="margin-right: 0.2222222222222222em;"></span></span><span class="base"><span class="strut" style="height: 0.76666em; vertical-align: -0.08333em;"></span><span class="mord">0</span><span class="mord">.</span><span class="mord">5</span><span class="mord">8</span><span class="mord">7</span><span class="mord">0</span><span class="mord">∗</span><span class="mord mathdefault">G</span><span class="mspace" style="margin-right: 0.2222222222222222em;"></span><span class="mbin">+</span><span class="mspace" style="margin-right: 0.2222222222222222em;"></span></span><span class="base"><span class="strut" style="height: 0.68333em; vertical-align: 0em;"></span><span class="mord">0</span><span class="mord">.</span><span class="mord">1</span><span class="mord">1</span><span class="mord">4</span><span class="mord">0</span><span class="mord">∗</span><span class="mord mathdefault" style="margin-right: 0.05017em;">B</span></span></span></span></span></span> 如此罢了。突然想起了之前一位同学在处理遥感影像的时候发现影像太大没法用MATLAB读取，ENVI直接死机的时候问我怎么做这个真彩色图，后来我和她说用ENVI的band math写一个波段运算把3个分量按比例送进去就行了。我觉得这个"送"是真的很传神，毕竟我喜欢称彩色是一种空间吗，哈哈哈！</p>

1.2 HSI空间

彩色模型是一种彩色感知空间，采用色度(Hue)，饱和度(Satutation)和亮度(Intense)直观的描述一种颜色空间。彩色空间基于两个重要的事实：
其一，亮度分量与图像的彩色信息无关；
其二，色度和饱和度分量与人对颜色的感受方式紧密相连。这些特点使得HSI彩色空间成为一种非常重要的以彩色处理为目的颜色空间的选择

顺便记下英文吧，对考研有帮助的!

色调和饱和度在HSI颜色模型中，点是任意颜色点。那个与红轴的夹角表示色调，矢量的长度为饱和。这个所有这些平面上所有颜色的强度都是由平面在垂直强度轴上的位置给出的

上面两段话是引自一篇硕士论文以及冈萨雷斯老师的书。
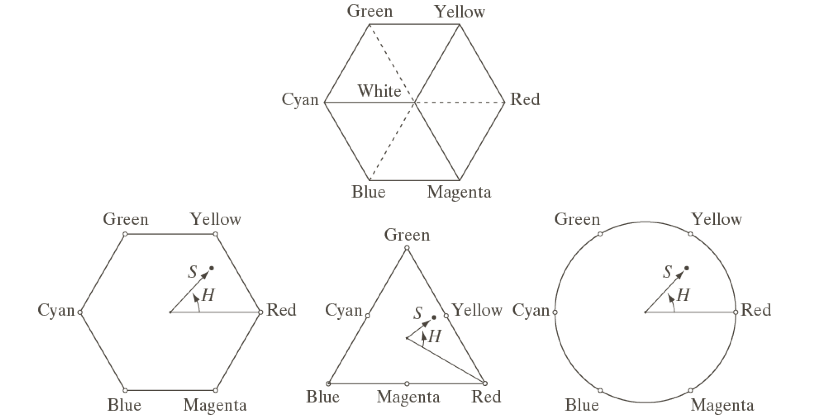
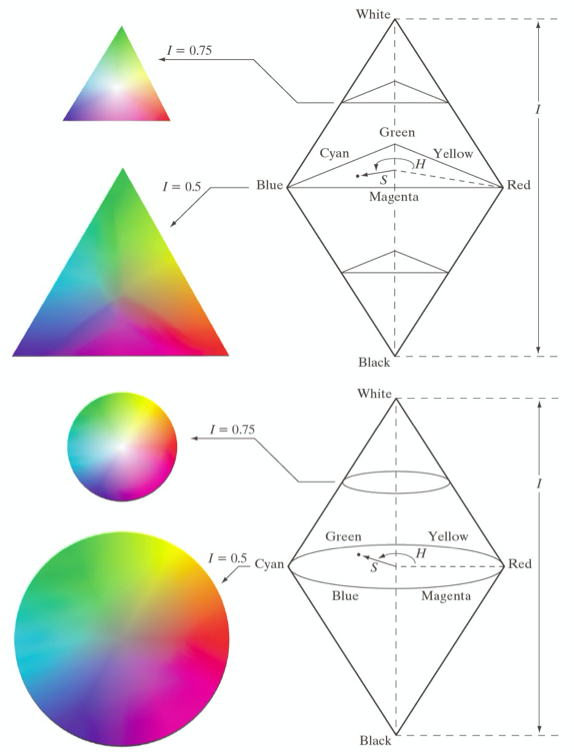
在这里插入图片描述
在这里插入图片描述

呃…其实感觉说了和没说没啥区别，毕竟通常都有封装好的API，如果实在没API自己写几个判断也能转化过来。

1.3 RGB和HIS的转化

  虽然俺确信这个百分之百不会考，但是既然写了文章就写下吧。

1.3.1 从RGB到HSI 

     H
    
    
     =
    
    
     
      {
     
     
      
       
        
         
          
           θ
          
          
           ,
          
         
        
       
       
        
         
          
           B
          
          
           ≤
          
          
           G
          
         
        
       
      
      
       
        
         
          
           360
          
          
           −
          
          
           θ
          
          
           ,
          
         
        
       
       
        
         
          
           B
          
          
           &gt;
          
          
           G
          
         
        
       
      
     
    
   
   
    H= <span class="MathJax_Preview" style="color: inherit; display: none;"></span><div class="MathJax_Display"><span class="MathJax MathJax_FullWidth" id="MathJax-Element-1-Frame" tabindex="0" data-mathml="<math xmlns=&quot;http://www.w3.org/1998/Math/MathML&quot; display=&quot;block&quot;><mrow><mo>{</mo><mtable columnalign=&quot;left left&quot; rowspacing=&quot;.2em&quot; columnspacing=&quot;1em&quot; displaystyle=&quot;false&quot;><mtr><mtd><mi>&amp;#x03B8;</mi><mo>,</mo></mtd><mtd><mi>B</mi><mo>&amp;#x2264;</mo><mi>G</mi></mtd></mtr><mtr><mtd><mn>360</mn><mo>&amp;#x2212;</mo><mi>&amp;#x03B8;</mi><mo>,</mo></mtd><mtd><mi>B</mi><mo>&amp;gt;</mo><mi>G</mi></mtd></mtr></mtable><mo fence=&quot;true&quot; stretchy=&quot;true&quot; symmetric=&quot;true&quot;></mo></mrow></math>" role="presentation" style="position: relative;"><nobr aria-hidden="true"><span class="math" id="MathJax-Span-1" style="width: 100%; display: inline-block; min-width: 8.558em;"><span style="display: inline-block; position: relative; width: 100%; height: 0px; font-size: 102%;"><span style="position: absolute; clip: rect(2.382em, 1008.36em, 5.115em, -999.997em); top: -3.997em; left: 0em; width: 100%;"><span class="mrow" id="MathJax-Span-2"><span style="display: inline-block; position: relative; width: 100%; height: 0px;"><span style="position: absolute; clip: rect(2.382em, 1008.36em, 5.115em, -999.997em); top: -3.997em; left: 50%; margin-left: -4.149em;"><span class="mrow" id="MathJax-Span-3"><span class="mo" id="MathJax-Span-4" style="vertical-align: 0em;"><span style="font-family: MathJax_Size3;">{</span></span><span class="mtable" id="MathJax-Span-5" style="padding-right: 0.154em; padding-left: 0.154em;"><span style="display: inline-block; position: relative; width: 7.292em; height: 0px;"><span style="position: absolute; clip: rect(2.584em, 1003.39em, 5.014em, -999.997em); top: -3.997em; left: 0em;"><span style="display: inline-block; position: relative; width: 3.445em; height: 0px;"><span style="position: absolute; width: 100%; clip: rect(3.141em, 1000.66em, 4.356em, -999.997em); top: -4.554em; left: 0em;"><span class="mtd" id="MathJax-Span-6"><span class="mrow" id="MathJax-Span-7"><span style="display: inline-block; position: relative; width: 100%; height: 0px;"><span style="position: absolute; clip: rect(3.141em, 1000.66em, 4.356em, -999.997em); top: -3.997em; left: 50%; margin-left: -0.352em;"><span class="mi" id="MathJax-Span-8" style="font-family: MathJax_Math-italic;">θ</span><span class="mo" id="MathJax-Span-9" style="font-family: MathJax_Main;">,</span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span></span></span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span><span style="position: absolute; width: 100%; clip: rect(3.141em, 1003.39em, 4.356em, -999.997em); top: -3.339em; left: 0em;"><span class="mtd" id="MathJax-Span-15"><span class="mrow" id="MathJax-Span-16"><span style="display: inline-block; position: relative; width: 100%; height: 0px;"><span style="position: absolute; clip: rect(3.141em, 1003.39em, 4.356em, -999.997em); top: -3.997em; left: 50%; margin-left: -1.719em;"><span class="mn" id="MathJax-Span-17" style="font-family: MathJax_Main;">360</span><span class="mo" id="MathJax-Span-18" style="font-family: MathJax_Main; padding-left: 0.205em;">−</span><span class="mi" id="MathJax-Span-19" style="font-family: MathJax_Math-italic; padding-left: 0.205em;">θ</span><span class="mo" id="MathJax-Span-20" style="font-family: MathJax_Main;">,</span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span></span></span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span><span style="position: absolute; clip: rect(2.584em, 1002.79em, 4.862em, -999.997em); top: -3.997em; left: 4.457em;"><span style="display: inline-block; position: relative; width: 2.837em; height: 0px;"><span style="position: absolute; width: 100%; clip: rect(3.141em, 1002.79em, 4.305em, -999.997em); top: -4.554em; left: 0em;"><span class="mtd" id="MathJax-Span-10"><span class="mrow" id="MathJax-Span-11"><span style="display: inline-block; position: relative; width: 100%; height: 0px;"><span style="position: absolute; clip: rect(3.141em, 1002.79em, 4.305em, -999.997em); top: -3.997em; left: 50%; margin-left: -1.415em;"><span class="mi" id="MathJax-Span-12" style="font-family: MathJax_Math-italic;">B</span><span class="mo" id="MathJax-Span-13" style="font-family: MathJax_Main; padding-left: 0.256em;">≤</span><span class="mi" id="MathJax-Span-14" style="font-family: MathJax_Math-italic; padding-left: 0.256em;">G</span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span></span></span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span><span style="position: absolute; width: 100%; clip: rect(3.141em, 1002.79em, 4.204em, -999.997em); top: -3.339em; left: 0em;"><span class="mtd" id="MathJax-Span-21"><span class="mrow" id="MathJax-Span-22"><span style="display: inline-block; position: relative; width: 100%; height: 0px;"><span style="position: absolute; clip: rect(3.141em, 1002.79em, 4.204em, -999.997em); top: -3.997em; left: 50%; margin-left: -1.415em;"><span class="mi" id="MathJax-Span-23" style="font-family: MathJax_Math-italic;">B</span><span class="mo" id="MathJax-Span-24" style="font-family: MathJax_Main; padding-left: 0.256em;">&gt;</span><span class="mi" id="MathJax-Span-25" style="font-family: MathJax_Math-italic; padding-left: 0.256em;">G</span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span></span></span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span></span><span class="mo" id="MathJax-Span-26"></span></span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span></span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span><span style="display: inline-block; overflow: hidden; vertical-align: -1.03em; border-left: 0px solid; width: 0px; height: 2.533em;"></span></span></nobr><span class="MJX_Assistive_MathML MJX_Assistive_MathML_Block" role="presentation"><math xmlns="http://www.w3.org/1998/Math/MathML" display="block"><mrow><mo>{</mo><mtable columnalign="left left" rowspacing=".2em" columnspacing="1em" displaystyle="false"><mtr><mtd><mi>θ</mi><mo>,</mo></mtd><mtd><mi>B</mi><mo>≤</mo><mi>G</mi></mtd></mtr><mtr><mtd><mn>360</mn><mo>−</mo><mi>θ</mi><mo>,</mo></mtd><mtd><mi>B</mi><mo>&gt;</mo><mi>G</mi></mtd></mtr></mtable><mo fence="true" stretchy="true" symmetric="true"></mo></mrow></math></span></span></div><script type="math/tex; mode=display" id="MathJax-Element-1">begin{cases} theta, & B le G \ 360 - theta, & B>G end{cases}</script>
   
  
 </span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.68333em; vertical-align: 0em;"></span><span class="mord mathdefault" style="margin-right: 0.08125em;">H</span><span class="mspace" style="margin-right: 0.2777777777777778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right: 0.2777777777777778em;"></span></span><span class="base"><span class="strut" style="height: 3.0000299999999998em; vertical-align: -1.25003em;"></span><span class="minner"><span class="mopen delimcenter" style="top: 0em;"><span class="delimsizing size4">{<!-- --></span></span><span class="mord"><span class="mtable"><span class="col-align-l"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 1.69em;"><span class="" style="top: -3.69em;"><span class="pstrut" style="height: 3.008em;"></span><span class="mord"><span class="mord mathdefault" style="margin-right: 0.02778em;">θ</span><span class="mpunct">,</span></span></span><span class="" style="top: -2.25em;"><span class="pstrut" style="height: 3.008em;"></span><span class="mord"><span class="mord">3</span><span class="mord">6</span><span class="mord">0</span><span class="mspace" style="margin-right: 0.2222222222222222em;"></span><span class="mbin">−</span><span class="mspace" style="margin-right: 0.2222222222222222em;"></span><span class="mord mathdefault" style="margin-right: 0.02778em;">θ</span><span class="mpunct">,</span></span></span></span><span class="vlist-s">​</span></span><span class="vlist-r"><span class="vlist" style="height: 1.19em;"><span class=""></span></span></span></span></span><span class="arraycolsep" style="width: 1em;"></span><span class="col-align-l"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 1.69em;"><span class="" style="top: -3.69em;"><span class="pstrut" style="height: 3.008em;"></span><span class="mord"><span class="mord mathdefault" style="margin-right: 0.05017em;">B</span><span class="mspace" style="margin-right: 0.2777777777777778em;"></span><span class="mrel">≤</span><span class="mspace" style="margin-right: 0.2777777777777778em;"></span><span class="mord mathdefault">G</span></span></span><span class="" style="top: -2.25em;"><span class="pstrut" style="height: 3.008em;"></span><span class="mord"><span class="mord mathdefault" style="margin-right: 0.05017em;">B</span><span class="mspace" style="margin-right: 0.2777777777777778em;"></span><span class="mrel">&gt;</span><span class="mspace" style="margin-right: 0.2777777777777778em;"></span><span class="mord mathdefault">G</span></span></span></span><span class="vlist-s">​</span></span><span class="vlist-r"><span class="vlist" style="height: 1.19em;"><span class=""></span></span></span></span></span></span></span><span class="mclose nulldelimiter"></span></span></span></span></span></span></span>其中<br data-filtered="filtered"> <span class="katex--display"><span class="katex-display"><span class="katex"><span class="katex-mathml">
 
  
   
    
     θ
    
    
     =
    
    
     arccos
    
    
     ⁡
    
    
     
      
       
        1
       
       
        2
       
      
      
       [
      
      
       (
      
      
       R
      
      
       −
      
      
       G
      
      
       )
      
      
       +
      
      
       (
      
      
       R
      
      
       −
      
      
       B
      
      
       )
      
      
       ]
      
     
     
      
       [
      
      
       (
      
      
       R
      
      
       −
      
      
       G
      
      
       
        )
       
       
        2
       
      
      
       +
      
      
       (
      
      
       R
      
      
       −
      
      
       B
      
      
       )
      
      
       (
      
      
       G
      
      
       −
      
      
       B
      
      
       )
      
      
       
        ]
       
       
        
         1
        
        
         /
        
        
         2
        
       
      
     
    
   
   
    theta = arccos { frac{ dfrac{1}{2} [ (R-G)+ (R- B)] }{ [(R-G)^2 + (R-B)(G-B)]^{1/2}} }
   
  
 </span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.69444em; vertical-align: 0em;"></span><span class="mord mathdefault" style="margin-right: 0.02778em;">θ</span><span class="mspace" style="margin-right: 0.2777777777777778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right: 0.2777777777777778em;"></span></span><span class="base"><span class="strut" style="height: 3.35144em; vertical-align: -0.954em;"></span><span class="mop">arccos</span><span class="mspace" style="margin-right: 0.16666666666666666em;"></span><span class="mord"><span class="mord"><span class="mopen nulldelimiter"></span><span class="mfrac"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 2.39744em;"><span class="" style="top: -2.61744em;"><span class="pstrut" style="height: 3.32144em;"></span><span class="mord"><span class="mopen">[</span><span class="mopen">(</span><span class="mord mathdefault" style="margin-right: 0.00773em;">R</span><span class="mspace" style="margin-right: 0.2222222222222222em;"></span><span class="mbin">−</span><span class="mspace" style="margin-right: 0.2222222222222222em;"></span><span class="mord mathdefault">G</span><span class="mclose"><span class="mclose">)</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.740108em;"><span class="" style="top: -2.9890000000000003em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">2</span></span></span></span></span></span></span></span><span class="mspace" style="margin-right: 0.2222222222222222em;"></span><span class="mbin">+</span><span class="mspace" style="margin-right: 0.2222222222222222em;"></span><span class="mopen">(</span><span class="mord mathdefault" style="margin-right: 0.00773em;">R</span><span class="mspace" style="margin-right: 0.2222222222222222em;"></span><span class="mbin">−</span><span class="mspace" style="margin-right: 0.2222222222222222em;"></span><span class="mord mathdefault" style="margin-right: 0.05017em;">B</span><span class="mclose">)</span><span class="mopen">(</span><span class="mord mathdefault">G</span><span class="mspace" style="margin-right: 0.2222222222222222em;"></span><span class="mbin">−</span><span class="mspace" style="margin-right: 0.2222222222222222em;"></span><span class="mord mathdefault" style="margin-right: 0.05017em;">B</span><span class="mclose">)</span><span class="mclose"><span class="mclose">]</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.814em;"><span class="" style="top: -2.989em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mtight">1</span><span class="mord mtight">/</span><span class="mord mtight">2</span></span></span></span></span></span></span></span></span></span></span><span class="" style="top: -3.55144em;"><span class="pstrut" style="height: 3.32144em;"></span><span class="frac-line" style="border-bottom-width: 0.04em;"></span></span><span class="" style="top: -4.3974400000000005em;"><span class="pstrut" style="height: 3.32144em;"></span><span class="mord"><span class="mord"><span class="mopen nulldelimiter"></span><span class="mfrac"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 1.32144em;"><span class="" style="top: -2.314em;"><span class="pstrut" style="height: 3em;"></span><span class="mord"><span class="mord">2</span></span></span><span class="" style="top: -3.23em;"><span class="pstrut" style="height: 3em;"></span><span class="frac-line" style="border-bottom-width: 0.04em;"></span></span><span class="" style="top: -3.677em;"><span class="pstrut" style="height: 3em;"></span><span class="mord"><span class="mord">1</span></span></span></span><span class="vlist-s">​</span></span><span class="vlist-r"><span class="vlist" style="height: 0.686em;"><span class=""></span></span></span></span></span><span class="mclose nulldelimiter"></span></span><span class="mopen">[</span><span class="mopen">(</span><span class="mord mathdefault" style="margin-right: 0.00773em;">R</span><span class="mspace" style="margin-right: 0.2222222222222222em;"></span><span class="mbin">−</span><span class="mspace" style="margin-right: 0.2222222222222222em;"></span><span class="mord mathdefault">G</span><span class="mclose">)</span><span class="mspace" style="margin-right: 0.2222222222222222em;"></span><span class="mbin">+</span><span class="mspace" style="margin-right: 0.2222222222222222em;"></span><span class="mopen">(</span><span class="mord mathdefault" style="margin-right: 0.00773em;">R</span><span class="mspace" style="margin-right: 0.2222222222222222em;"></span><span class="mbin">−</span><span class="mspace" style="margin-right: 0.2222222222222222em;"></span><span class="mord mathdefault" style="margin-right: 0.05017em;">B</span><span class="mclose">)</span><span class="mclose">]</span></span></span></span><span class="vlist-s">​</span></span><span class="vlist-r"><span class="vlist" style="height: 0.954em;"><span class=""></span></span></span></span></span><span class="mclose nulldelimiter"></span></span></span></span></span></span></span></span><br data-filtered="filtered"> 饱和度(S)由下列公式给出<br data-filtered="filtered"> <span class="katex--display"><span class="katex-display"><span class="katex"><span class="katex-mathml">
 
  
   
    
     S
    
    
     =
    
    
     1
    
    
     −
    
    
     
      3
     
     
      
       (
      
      
       R
      
      
       +
      
      
       G
      
      
       +
      
      
       B
      
      
       )
      
     
    
    
     [
    
    
     min
    
    
     ⁡
    
    
     (
    
    
     R
    
    
     ,
    
    
     G
    
    
     ,
    
    
     B
    
    
     )
    
    
     ]
    
   
   
    S = 1 - frac{3}{(R+G+B)}[min(R,G,B)]
   
  
 </span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.68333em; vertical-align: 0em;"></span><span class="mord mathdefault" style="margin-right: 0.05764em;">S</span><span class="mspace" style="margin-right: 0.2777777777777778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right: 0.2777777777777778em;"></span></span><span class="base"><span class="strut" style="height: 0.72777em; vertical-align: -0.08333em;"></span><span class="mord">1</span><span class="mspace" style="margin-right: 0.2222222222222222em;"></span><span class="mbin">−</span><span class="mspace" style="margin-right: 0.2222222222222222em;"></span></span><span class="base"><span class="strut" style="height: 2.25744em; vertical-align: -0.936em;"></span><span class="mord"><span class="mopen nulldelimiter"></span><span class="mfrac"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 1.32144em;"><span class="" style="top: -2.314em;"><span class="pstrut" style="height: 3em;"></span><span class="mord"><span class="mopen">(</span><span class="mord mathdefault" style="margin-right: 0.00773em;">R</span><span class="mspace" style="margin-right: 0.2222222222222222em;"></span><span class="mbin">+</span><span class="mspace" style="margin-right: 0.2222222222222222em;"></span><span class="mord mathdefault">G</span><span class="mspace" style="margin-right: 0.2222222222222222em;"></span><span class="mbin">+</span><span class="mspace" style="margin-right: 0.2222222222222222em;"></span><span class="mord mathdefault" style="margin-right: 0.05017em;">B</span><span class="mclose">)</span></span></span><span class="" style="top: -3.23em;"><span class="pstrut" style="height: 3em;"></span><span class="frac-line" style="border-bottom-width: 0.04em;"></span></span><span class="" style="top: -3.677em;"><span class="pstrut" style="height: 3em;"></span><span class="mord"><span class="mord">3</span></span></span></span><span class="vlist-s">​</span></span><span class="vlist-r"><span class="vlist" style="height: 0.936em;"><span class=""></span></span></span></span></span><span class="mclose nulldelimiter"></span></span><span class="mopen">[</span><span class="mop">min</span><span class="mopen">(</span><span class="mord mathdefault" style="margin-right: 0.00773em;">R</span><span class="mpunct">,</span><span class="mspace" style="margin-right: 0.16666666666666666em;"></span><span class="mord mathdefault">G</span><span class="mpunct">,</span><span class="mspace" style="margin-right: 0.16666666666666666em;"></span><span class="mord mathdefault" style="margin-right: 0.05017em;">B</span><span class="mclose">)</span><span class="mclose">]</span></span></span></span></span></span><br data-filtered="filtered"> 强度(I)由下列公式给出<br data-filtered="filtered"> <span class="katex--display"><span class="katex-display"><span class="katex"><span class="katex-mathml">
 
  
   
    
     I
    
    
     =
    
    
     
      1
     
     
      3
     
    
    
     (
    
    
     R
    
    
     +
    
    
     G
    
    
     +
    
    
     B
    
    
     )
    
   
   
    I = dfrac{1}{3} (R+G+B)
   
  
 </span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.68333em; vertical-align: 0em;"></span><span class="mord mathdefault" style="margin-right: 0.07847em;">I</span><span class="mspace" style="margin-right: 0.2777777777777778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right: 0.2777777777777778em;"></span></span><span class="base"><span class="strut" style="height: 2.00744em; vertical-align: -0.686em;"></span><span class="mord"><span class="mopen nulldelimiter"></span><span class="mfrac"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 1.32144em;"><span class="" style="top: -2.314em;"><span class="pstrut" style="height: 3em;"></span><span class="mord"><span class="mord">3</span></span></span><span class="" style="top: -3.23em;"><span class="pstrut" style="height: 3em;"></span><span class="frac-line" style="border-bottom-width: 0.04em;"></span></span><span class="" style="top: -3.677em;"><span class="pstrut" style="height: 3em;"></span><span class="mord"><span class="mord">1</span></span></span></span><span class="vlist-s">​</span></span><span class="vlist-r"><span class="vlist" style="height: 0.686em;"><span class=""></span></span></span></span></span><span class="mclose nulldelimiter"></span></span><span class="mopen">(</span><span class="mord mathdefault" style="margin-right: 0.00773em;">R</span><span class="mspace" style="margin-right: 0.2222222222222222em;"></span><span class="mbin">+</span><span class="mspace" style="margin-right: 0.2222222222222222em;"></span></span><span class="base"><span class="strut" style="height: 0.76666em; vertical-align: -0.08333em;"></span><span class="mord mathdefault">G</span><span class="mspace" style="margin-right: 0.2222222222222222em;"></span><span class="mbin">+</span><span class="mspace" style="margin-right: 0.2222222222222222em;"></span></span><span class="base"><span class="strut" style="height: 1em; vertical-align: -0.25em;"></span><span class="mord mathdefault" style="margin-right: 0.05017em;">B</span><span class="mclose">)</span></span></span></span></span></span></p>

1.3.2 从HSI到RGB

   在 

    [
   
   
    0
   
   
    ,
   
   
    1
   
   
    ]
   
  
  
   [0,1]
  
 
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 1em; vertical-align: -0.25em;"></span><span class="mopen">[</span><span class="mord">0</span><span class="mpunct">,</span><span class="mspace" style="margin-right: 0.16666666666666666em;"></span><span class="mord">1</span><span class="mclose">]</span></span></span></span></span>内给出HSI值，现在我们想要在相同的值域找到对应的RGB值。可用的公式取决于H的值。在原色分隔中有3个相隔<span class="katex--inline"><span class="katex"><span class="katex-mathml">

 
  
   
    12
   
   
    
     0
    
    
     ∘
    
   
  
  
   120^{circ}
  
 
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.674115em; vertical-align: 0em;"></span><span class="mord">1</span><span class="mord">2</span><span class="mord"><span class="mord">0</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.674115em;"><span class="" style="top: -3.063em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mtight">∘</span></span></span></span></span></span></span></span></span></span></span></span></span>扇形区间。我们从H乘以<span class="katex--inline"><span class="katex"><span class="katex-mathml">

 
  
   
    36
   
   
    
     0
    
    
     ∘
    
   
  
  
   360^{circ}
  
 
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.674115em; vertical-align: 0em;"></span><span class="mord">3</span><span class="mord">6</span><span class="mord"><span class="mord">0</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.674115em;"><span class="" style="top: -3.063em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mtight">∘</span></span></span></span></span></span></span></span></span></span></span></span></span>开始，这时的色调值调回到范围<span class="katex--inline"><span class="katex"><span class="katex-mathml">

 
  
   
    [
   
   
    
     0
    
    
     ∘
    
   
   
    ,
   
   
    36
   
   
    
     0
    
    
     ∘
    
   
   
    ]
   
  
  
   [0^{circ},360^{circ}]
  
 
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 1em; vertical-align: -0.25em;"></span><span class="mopen">[</span><span class="mord"><span class="mord">0</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.674115em;"><span class="" style="top: -3.063em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mtight">∘</span></span></span></span></span></span></span></span></span><span class="mpunct">,</span><span class="mspace" style="margin-right: 0.16666666666666666em;"></span><span class="mord">3</span><span class="mord">6</span><span class="mord"><span class="mord">0</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.674115em;"><span class="" style="top: -3.063em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mtight">∘</span></span></span></span></span></span></span></span></span><span class="mclose">]</span></span></span></span></span></p>

RG扇区 

     (
    
    
     
      0
     
     
      ∘
     
    
    
     ≤
    
    
     H
    
    
     ≤
    
    
     12
    
    
     
      0
     
     
      ∘
     
    
    
     )
    
   
   
    (0^{circ} le H le 120^{circ})
   
  
 </span><span class="katex-html"><span class="base"><span class="strut" style="height: 1em; vertical-align: -0.25em;"></span><span class="mopen">(</span><span class="mord"><span class="mord">0</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.674115em;"><span class="" style="top: -3.063em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mtight">∘</span></span></span></span></span></span></span></span></span><span class="mspace" style="margin-right: 0.2777777777777778em;"></span><span class="mrel">≤</span><span class="mspace" style="margin-right: 0.2777777777777778em;"></span></span><span class="base"><span class="strut" style="height: 0.8193em; vertical-align: -0.13597em;"></span><span class="mord mathdefault" style="margin-right: 0.08125em;">H</span><span class="mspace" style="margin-right: 0.2777777777777778em;"></span><span class="mrel">≤</span><span class="mspace" style="margin-right: 0.2777777777777778em;"></span></span><span class="base"><span class="strut" style="height: 1em; vertical-align: -0.25em;"></span><span class="mord">1</span><span class="mord">2</span><span class="mord"><span class="mord">0</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.674115em;"><span class="" style="top: -3.063em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mtight">∘</span></span></span></span></span></span></span></span></span><span class="mclose">)</span></span></span></span></span>:当<span class="katex--inline"><span class="katex"><span class="katex-mathml">
 
  
   
    
     H
    
   
   
    H
   
  
 </span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.68333em; vertical-align: 0em;"></span><span class="mord mathdefault" style="margin-right: 0.08125em;">H</span></span></span></span></span>的值在该扇区中时，RGB分量由以下公式给出。</font><br data-filtered="filtered"> <span class="katex--display"><span class="katex-display"><span class="katex"><span class="katex-mathml">
 
  
   
    
     B
    
    
     =
    
    
     I
    
    
     (
    
    
     1
    
    
     −
    
    
     S
    
    
     )
    
   
   
    B = I(1-S)
   
  
 </span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.68333em; vertical-align: 0em;"></span><span class="mord mathdefault" style="margin-right: 0.05017em;">B</span><span class="mspace" style="margin-right: 0.2777777777777778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right: 0.2777777777777778em;"></span></span><span class="base"><span class="strut" style="height: 1em; vertical-align: -0.25em;"></span><span class="mord mathdefault" style="margin-right: 0.07847em;">I</span><span class="mopen">(</span><span class="mord">1</span><span class="mspace" style="margin-right: 0.2222222222222222em;"></span><span class="mbin">−</span><span class="mspace" style="margin-right: 0.2222222222222222em;"></span></span><span class="base"><span class="strut" style="height: 1em; vertical-align: -0.25em;"></span><span class="mord mathdefault" style="margin-right: 0.05764em;">S</span><span class="mclose">)</span></span></span></span></span></span><span class="katex--display"><span class="katex-display"><span class="katex"><span class="katex-mathml">
 
  
   
    
     R
    
    
     =
    
    
     I
    
    
     [
    
    
     1
    
    
     +
    
    
     
      
       S
      
      
       cos
      
      
       ⁡
      
      
       H
      
     
     
      
       cos
      
      
       ⁡
      
      
       (
      
      
       6
      
      
       
        0
       
       
        ∘
       
      
      
       −
      
      
       H
      
      
       )
      
     
    
    
     ]
    
   
   
    R = I[1 + frac{Scos H}{cos(60^{circ} -H)}]
   
  
 </span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.68333em; vertical-align: 0em;"></span><span class="mord mathdefault" style="margin-right: 0.00773em;">R</span><span class="mspace" style="margin-right: 0.2777777777777778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right: 0.2777777777777778em;"></span></span><span class="base"><span class="strut" style="height: 1em; vertical-align: -0.25em;"></span><span class="mord mathdefault" style="margin-right: 0.07847em;">I</span><span class="mopen">[</span><span class="mord">1</span><span class="mspace" style="margin-right: 0.2222222222222222em;"></span><span class="mbin">+</span><span class="mspace" style="margin-right: 0.2222222222222222em;"></span></span><span class="base"><span class="strut" style="height: 2.29633em; vertical-align: -0.936em;"></span><span class="mord"><span class="mopen nulldelimiter"></span><span class="mfrac"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 1.36033em;"><span class="" style="top: -2.314em;"><span class="pstrut" style="height: 3em;"></span><span class="mord"><span class="mop">cos</span><span class="mopen">(</span><span class="mord">6</span><span class="mord"><span class="mord">0</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.600115em;"><span class="" style="top: -2.9890000000000003em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mtight">∘</span></span></span></span></span></span></span></span></span><span class="mspace" style="margin-right: 0.2222222222222222em;"></span><span class="mbin">−</span><span class="mspace" style="margin-right: 0.2222222222222222em;"></span><span class="mord mathdefault" style="margin-right: 0.08125em;">H</span><span class="mclose">)</span></span></span><span class="" style="top: -3.23em;"><span class="pstrut" style="height: 3em;"></span><span class="frac-line" style="border-bottom-width: 0.04em;"></span></span><span class="" style="top: -3.677em;"><span class="pstrut" style="height: 3em;"></span><span class="mord"><span class="mord mathdefault" style="margin-right: 0.05764em;">S</span><span class="mspace" style="margin-right: 0.16666666666666666em;"></span><span class="mop">cos</span><span class="mspace" style="margin-right: 0.16666666666666666em;"></span><span class="mord mathdefault" style="margin-right: 0.08125em;">H</span></span></span></span><span class="vlist-s">​</span></span><span class="vlist-r"><span class="vlist" style="height: 0.936em;"><span class=""></span></span></span></span></span><span class="mclose nulldelimiter"></span></span><span class="mclose">]</span></span></span></span></span></span> <span class="katex--display"><span class="katex-display"><span class="katex"><span class="katex-mathml">
 
  
   
    
     G
    
    
     =
    
    
     3
    
    
     I
    
    
     −
    
    
     (
    
    
     R
    
    
     +
    
    
     B
    
    
     )
    
   
   
    G = 3I - (R+B)
   
  
 </span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.68333em; vertical-align: 0em;"></span><span class="mord mathdefault">G</span><span class="mspace" style="margin-right: 0.2777777777777778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right: 0.2777777777777778em;"></span></span><span class="base"><span class="strut" style="height: 0.76666em; vertical-align: -0.08333em;"></span><span class="mord">3</span><span class="mord mathdefault" style="margin-right: 0.07847em;">I</span><span class="mspace" style="margin-right: 0.2222222222222222em;"></span><span class="mbin">−</span><span class="mspace" style="margin-right: 0.2222222222222222em;"></span></span><span class="base"><span class="strut" style="height: 1em; vertical-align: -0.25em;"></span><span class="mopen">(</span><span class="mord mathdefault" style="margin-right: 0.00773em;">R</span><span class="mspace" style="margin-right: 0.2222222222222222em;"></span><span class="mbin">+</span><span class="mspace" style="margin-right: 0.2222222222222222em;"></span></span><span class="base"><span class="strut" style="height: 1em; vertical-align: -0.25em;"></span><span class="mord mathdefault" style="margin-right: 0.05017em;">B</span><span class="mclose">)</span></span></span></span></span></span></p>

GB扇区 

     (
    
    
     12
    
    
     
      0
     
     
      ∘
     
    
    
     ≤
    
    
     H
    
    
     ≤
    
    
     24
    
    
     
      0
     
     
      ∘
     
    
    
     )
    
   
   
    (120^{circ} le H le 240^{circ})
   
  
 </span><span class="katex-html"><span class="base"><span class="strut" style="height: 1em; vertical-align: -0.25em;"></span><span class="mopen">(</span><span class="mord">1</span><span class="mord">2</span><span class="mord"><span class="mord">0</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.674115em;"><span class="" style="top: -3.063em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mtight">∘</span></span></span></span></span></span></span></span></span><span class="mspace" style="margin-right: 0.2777777777777778em;"></span><span class="mrel">≤</span><span class="mspace" style="margin-right: 0.2777777777777778em;"></span></span><span class="base"><span class="strut" style="height: 0.8193em; vertical-align: -0.13597em;"></span><span class="mord mathdefault" style="margin-right: 0.08125em;">H</span><span class="mspace" style="margin-right: 0.2777777777777778em;"></span><span class="mrel">≤</span><span class="mspace" style="margin-right: 0.2777777777777778em;"></span></span><span class="base"><span class="strut" style="height: 1em; vertical-align: -0.25em;"></span><span class="mord">2</span><span class="mord">4</span><span class="mord"><span class="mord">0</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.674115em;"><span class="" style="top: -3.063em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mtight">∘</span></span></span></span></span></span></span></span></span><span class="mclose">)</span></span></span></span></span>:当<span class="katex--inline"><span class="katex"><span class="katex-mathml">
 
  
   
    
     H
    
   
   
    H
   
  
 </span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.68333em; vertical-align: 0em;"></span><span class="mord mathdefault" style="margin-right: 0.08125em;">H</span></span></span></span></span>的值在该扇区中时，RGB分量由以下公式给出,则从<span class="katex--inline"><span class="katex"><span class="katex-mathml">
 
  
   
    
     H
    
   
   
    H
   
  
 </span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.68333em; vertical-align: 0em;"></span><span class="mord mathdefault" style="margin-right: 0.08125em;">H</span></span></span></span></span>中减去<span class="katex--inline"><span class="katex"><span class="katex-mathml">
 
  
   
    
     12
    
    
     
      0
     
     
      ∘
     
    
   
   
    120^{circ}
   
  
 </span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.674115em; vertical-align: 0em;"></span><span class="mord">1</span><span class="mord">2</span><span class="mord"><span class="mord">0</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.674115em;"><span class="" style="top: -3.063em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mtight">∘</span></span></span></span></span></span></span></span></span></span></span></span></span>,即 </font><br data-filtered="filtered"> <span class="katex--display"><span class="katex-display"><span class="katex"><span class="katex-mathml">
 
  
   
    
     H
    
    
     =
    
    
     H
    
    
     −
    
    
     12
    
    
     
      0
     
     
      ∘
     
    
   
   
    H = H - 120^{circ}
   
  
 </span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.68333em; vertical-align: 0em;"></span><span class="mord mathdefault" style="margin-right: 0.08125em;">H</span><span class="mspace" style="margin-right: 0.2777777777777778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right: 0.2777777777777778em;"></span></span><span class="base"><span class="strut" style="height: 0.76666em; vertical-align: -0.08333em;"></span><span class="mord mathdefault" style="margin-right: 0.08125em;">H</span><span class="mspace" style="margin-right: 0.2222222222222222em;"></span><span class="mbin">−</span><span class="mspace" style="margin-right: 0.2222222222222222em;"></span></span><span class="base"><span class="strut" style="height: 0.724115em; vertical-align: 0em;"></span><span class="mord">1</span><span class="mord">2</span><span class="mord"><span class="mord">0</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.724115em;"><span class="" style="top: -3.113em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mtight">∘</span></span></span></span></span></span></span></span></span></span></span></span></span></span><span class="katex--display"><span class="katex-display"><span class="katex"><span class="katex-mathml">
 
  
   
    
     R
    
    
     =
    
    
     I
    
    
     (
    
    
     1
    
    
     −
    
    
     S
    
    
     )
    
   
   
    R = I(1-S)
   
  
 </span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.68333em; vertical-align: 0em;"></span><span class="mord mathdefault" style="margin-right: 0.00773em;">R</span><span class="mspace" style="margin-right: 0.2777777777777778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right: 0.2777777777777778em;"></span></span><span class="base"><span class="strut" style="height: 1em; vertical-align: -0.25em;"></span><span class="mord mathdefault" style="margin-right: 0.07847em;">I</span><span class="mopen">(</span><span class="mord">1</span><span class="mspace" style="margin-right: 0.2222222222222222em;"></span><span class="mbin">−</span><span class="mspace" style="margin-right: 0.2222222222222222em;"></span></span><span class="base"><span class="strut" style="height: 1em; vertical-align: -0.25em;"></span><span class="mord mathdefault" style="margin-right: 0.05764em;">S</span><span class="mclose">)</span></span></span></span></span></span><span class="katex--display"><span class="katex-display"><span class="katex"><span class="katex-mathml">
 
  
   
    
     G
    
    
     =
    
    
     I
    
    
     [
    
    
     1
    
    
     +
    
    
     
      
       S
      
      
       cos
      
      
       ⁡
      
      
       H
      
     
     
      
       cos
      
      
       ⁡
      
      
       (
      
      
       6
      
      
       
        0
       
       
        ∘
       
      
      
       −
      
      
       H
      
      
       )
      
     
    
    
     ]
    
   
   
    G = I[1 + frac{Scos H}{cos(60^{circ} -H)}]
   
  
 </span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.68333em; vertical-align: 0em;"></span><span class="mord mathdefault">G</span><span class="mspace" style="margin-right: 0.2777777777777778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right: 0.2777777777777778em;"></span></span><span class="base"><span class="strut" style="height: 1em; vertical-align: -0.25em;"></span><span class="mord mathdefault" style="margin-right: 0.07847em;">I</span><span class="mopen">[</span><span class="mord">1</span><span class="mspace" style="margin-right: 0.2222222222222222em;"></span><span class="mbin">+</span><span class="mspace" style="margin-right: 0.2222222222222222em;"></span></span><span class="base"><span class="strut" style="height: 2.29633em; vertical-align: -0.936em;"></span><span class="mord"><span class="mopen nulldelimiter"></span><span class="mfrac"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 1.36033em;"><span class="" style="top: -2.314em;"><span class="pstrut" style="height: 3em;"></span><span class="mord"><span class="mop">cos</span><span class="mopen">(</span><span class="mord">6</span><span class="mord"><span class="mord">0</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.600115em;"><span class="" style="top: -2.9890000000000003em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mtight">∘</span></span></span></span></span></span></span></span></span><span class="mspace" style="margin-right: 0.2222222222222222em;"></span><span class="mbin">−</span><span class="mspace" style="margin-right: 0.2222222222222222em;"></span><span class="mord mathdefault" style="margin-right: 0.08125em;">H</span><span class="mclose">)</span></span></span><span class="" style="top: -3.23em;"><span class="pstrut" style="height: 3em;"></span><span class="frac-line" style="border-bottom-width: 0.04em;"></span></span><span class="" style="top: -3.677em;"><span class="pstrut" style="height: 3em;"></span><span class="mord"><span class="mord mathdefault" style="margin-right: 0.05764em;">S</span><span class="mspace" style="margin-right: 0.16666666666666666em;"></span><span class="mop">cos</span><span class="mspace" style="margin-right: 0.16666666666666666em;"></span><span class="mord mathdefault" style="margin-right: 0.08125em;">H</span></span></span></span><span class="vlist-s">​</span></span><span class="vlist-r"><span class="vlist" style="height: 0.936em;"><span class=""></span></span></span></span></span><span class="mclose nulldelimiter"></span></span><span class="mclose">]</span></span></span></span></span></span><span class="katex--display"><span class="katex-display"><span class="katex"><span class="katex-mathml">
 
  
   
    
     B
    
    
     =
    
    
     3
    
    
     I
    
    
     −
    
    
     (
    
    
     R
    
    
     +
    
    
     G
    
    
     )
    
   
   
    B = 3I - (R+G) 
   
  
 </span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.68333em; vertical-align: 0em;"></span><span class="mord mathdefault" style="margin-right: 0.05017em;">B</span><span class="mspace" style="margin-right: 0.2777777777777778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right: 0.2777777777777778em;"></span></span><span class="base"><span class="strut" style="height: 0.76666em; vertical-align: -0.08333em;"></span><span class="mord">3</span><span class="mord mathdefault" style="margin-right: 0.07847em;">I</span><span class="mspace" style="margin-right: 0.2222222222222222em;"></span><span class="mbin">−</span><span class="mspace" style="margin-right: 0.2222222222222222em;"></span></span><span class="base"><span class="strut" style="height: 1em; vertical-align: -0.25em;"></span><span class="mopen">(</span><span class="mord mathdefault" style="margin-right: 0.00773em;">R</span><span class="mspace" style="margin-right: 0.2222222222222222em;"></span><span class="mbin">+</span><span class="mspace" style="margin-right: 0.2222222222222222em;"></span></span><span class="base"><span class="strut" style="height: 1em; vertical-align: -0.25em;"></span><span class="mord mathdefault">G</span><span class="mclose">)</span></span></span></span></span></span></p>

BR扇区 

     (
    
    
     24
    
    
     
      0
     
     
      ∘
     
    
    
     ≤
    
    
     H
    
    
     ≤
    
    
     36
    
    
     
      0
     
     
      ∘
     
    
    
     )
    
   
   
    (240^{circ} le H le 360^{circ})
   
  
 </span><span class="katex-html"><span class="base"><span class="strut" style="height: 1em; vertical-align: -0.25em;"></span><span class="mopen">(</span><span class="mord">2</span><span class="mord">4</span><span class="mord"><span class="mord">0</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.674115em;"><span class="" style="top: -3.063em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mtight">∘</span></span></span></span></span></span></span></span></span><span class="mspace" style="margin-right: 0.2777777777777778em;"></span><span class="mrel">≤</span><span class="mspace" style="margin-right: 0.2777777777777778em;"></span></span><span class="base"><span class="strut" style="height: 0.8193em; vertical-align: -0.13597em;"></span><span class="mord mathdefault" style="margin-right: 0.08125em;">H</span><span class="mspace" style="margin-right: 0.2777777777777778em;"></span><span class="mrel">≤</span><span class="mspace" style="margin-right: 0.2777777777777778em;"></span></span><span class="base"><span class="strut" style="height: 1em; vertical-align: -0.25em;"></span><span class="mord">3</span><span class="mord">6</span><span class="mord"><span class="mord">0</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.674115em;"><span class="" style="top: -3.063em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mtight">∘</span></span></span></span></span></span></span></span></span><span class="mclose">)</span></span></span></span></span>:当<span class="katex--inline"><span class="katex"><span class="katex-mathml">
 
  
   
    
     H
    
   
   
    H
   
  
 </span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.68333em; vertical-align: 0em;"></span><span class="mord mathdefault" style="margin-right: 0.08125em;">H</span></span></span></span></span>的值在该扇区中时，RGB分量由以下公式给出,则从<span class="katex--inline"><span class="katex"><span class="katex-mathml">
 
  
   
    
     H
    
   
   
    H
   
  
 </span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.68333em; vertical-align: 0em;"></span><span class="mord mathdefault" style="margin-right: 0.08125em;">H</span></span></span></span></span>中减去<span class="katex--inline"><span class="katex"><span class="katex-mathml">
 
  
   
    
     24
    
    
     
      0
     
     
      ∘
     
    
   
   
    240^{circ}
   
  
 </span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.674115em; vertical-align: 0em;"></span><span class="mord">2</span><span class="mord">4</span><span class="mord"><span class="mord">0</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.674115em;"><span class="" style="top: -3.063em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mtight">∘</span></span></span></span></span></span></span></span></span></span></span></span></span>,即</font><br data-filtered="filtered"> <span class="katex--display"><span class="katex-display"><span class="katex"><span class="katex-mathml">
 
  
   
    
     H
    
    
     =
    
    
     H
    
    
     −
    
    
     24
    
    
     
      0
     
     
      ∘
     
    
   
   
     H = H - 240^{circ}
   
  
 </span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.68333em; vertical-align: 0em;"></span><span class="mord mathdefault" style="margin-right: 0.08125em;">H</span><span class="mspace" style="margin-right: 0.2777777777777778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right: 0.2777777777777778em;"></span></span><span class="base"><span class="strut" style="height: 0.76666em; vertical-align: -0.08333em;"></span><span class="mord mathdefault" style="margin-right: 0.08125em;">H</span><span class="mspace" style="margin-right: 0.2222222222222222em;"></span><span class="mbin">−</span><span class="mspace" style="margin-right: 0.2222222222222222em;"></span></span><span class="base"><span class="strut" style="height: 0.724115em; vertical-align: 0em;"></span><span class="mord">2</span><span class="mord">4</span><span class="mord"><span class="mord">0</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.724115em;"><span class="" style="top: -3.113em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mtight">∘</span></span></span></span></span></span></span></span></span></span></span></span></span></span><span class="katex--display"><span class="katex-display"><span class="katex"><span class="katex-mathml">
 
  
   
    
     G
    
    
     =
    
    
     I
    
    
     (
    
    
     1
    
    
     −
    
    
     S
    
    
     )
    
   
   
     G = I(1-S)
   
  
 </span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.68333em; vertical-align: 0em;"></span><span class="mord mathdefault">G</span><span class="mspace" style="margin-right: 0.2777777777777778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right: 0.2777777777777778em;"></span></span><span class="base"><span class="strut" style="height: 1em; vertical-align: -0.25em;"></span><span class="mord mathdefault" style="margin-right: 0.07847em;">I</span><span class="mopen">(</span><span class="mord">1</span><span class="mspace" style="margin-right: 0.2222222222222222em;"></span><span class="mbin">−</span><span class="mspace" style="margin-right: 0.2222222222222222em;"></span></span><span class="base"><span class="strut" style="height: 1em; vertical-align: -0.25em;"></span><span class="mord mathdefault" style="margin-right: 0.05764em;">S</span><span class="mclose">)</span></span></span></span></span></span><span class="katex--display"><span class="katex-display"><span class="katex"><span class="katex-mathml">
 
  
   
    
     B
    
    
     =
    
    
     I
    
    
     [
    
    
     1
    
    
     +
    
    
     
      
       S
      
      
       cos
      
      
       ⁡
      
      
       H
      
     
     
      
       cos
      
      
       ⁡
      
      
       (
      
      
       6
      
      
       
        0
       
       
        ∘
       
      
      
       −
      
      
       H
      
      
       )
      
     
    
    
     ]
    
   
   
    B = I[1 + frac{Scos H}{cos(60^{circ} -H)}]
   
  
 </span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.68333em; vertical-align: 0em;"></span><span class="mord mathdefault" style="margin-right: 0.05017em;">B</span><span class="mspace" style="margin-right: 0.2777777777777778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right: 0.2777777777777778em;"></span></span><span class="base"><span class="strut" style="height: 1em; vertical-align: -0.25em;"></span><span class="mord mathdefault" style="margin-right: 0.07847em;">I</span><span class="mopen">[</span><span class="mord">1</span><span class="mspace" style="margin-right: 0.2222222222222222em;"></span><span class="mbin">+</span><span class="mspace" style="margin-right: 0.2222222222222222em;"></span></span><span class="base"><span class="strut" style="height: 2.29633em; vertical-align: -0.936em;"></span><span class="mord"><span class="mopen nulldelimiter"></span><span class="mfrac"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 1.36033em;"><span class="" style="top: -2.314em;"><span class="pstrut" style="height: 3em;"></span><span class="mord"><span class="mop">cos</span><span class="mopen">(</span><span class="mord">6</span><span class="mord"><span class="mord">0</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.600115em;"><span class="" style="top: -2.9890000000000003em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mtight">∘</span></span></span></span></span></span></span></span></span><span class="mspace" style="margin-right: 0.2222222222222222em;"></span><span class="mbin">−</span><span class="mspace" style="margin-right: 0.2222222222222222em;"></span><span class="mord mathdefault" style="margin-right: 0.08125em;">H</span><span class="mclose">)</span></span></span><span class="" style="top: -3.23em;"><span class="pstrut" style="height: 3em;"></span><span class="frac-line" style="border-bottom-width: 0.04em;"></span></span><span class="" style="top: -3.677em;"><span class="pstrut" style="height: 3em;"></span><span class="mord"><span class="mord mathdefault" style="margin-right: 0.05764em;">S</span><span class="mspace" style="margin-right: 0.16666666666666666em;"></span><span class="mop">cos</span><span class="mspace" style="margin-right: 0.16666666666666666em;"></span><span class="mord mathdefault" style="margin-right: 0.08125em;">H</span></span></span></span><span class="vlist-s">​</span></span><span class="vlist-r"><span class="vlist" style="height: 0.936em;"><span class=""></span></span></span></span></span><span class="mclose nulldelimiter"></span></span><span class="mclose">]</span></span></span></span></span></span><span class="katex--display"><span class="katex-display"><span class="katex"><span class="katex-mathml">
 
  
   
    
     R
    
    
     =
    
    
     3
    
    
     I
    
    
     −
    
    
     (
    
    
     G
    
    
     +
    
    
     B
    
    
     )
    
   
   
    R = 3I - (G+B) 
   
  
 </span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.68333em; vertical-align: 0em;"></span><span class="mord mathdefault" style="margin-right: 0.00773em;">R</span><span class="mspace" style="margin-right: 0.2777777777777778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right: 0.2777777777777778em;"></span></span><span class="base"><span class="strut" style="height: 0.76666em; vertical-align: -0.08333em;"></span><span class="mord">3</span><span class="mord mathdefault" style="margin-right: 0.07847em;">I</span><span class="mspace" style="margin-right: 0.2222222222222222em;"></span><span class="mbin">−</span><span class="mspace" style="margin-right: 0.2222222222222222em;"></span></span><span class="base"><span class="strut" style="height: 1em; vertical-align: -0.25em;"></span><span class="mopen">(</span><span class="mord mathdefault">G</span><span class="mspace" style="margin-right: 0.2222222222222222em;"></span><span class="mbin">+</span><span class="mspace" style="margin-right: 0.2222222222222222em;"></span></span><span class="base"><span class="strut" style="height: 1em; vertical-align: -0.25em;"></span><span class="mord mathdefault" style="margin-right: 0.05017em;">B</span><span class="mclose">)</span></span></span></span></span></span></p>

其实可以看到就是一个过圆环走规律的过程，缺谁我那么一个分量值就是 

    I
   
   
    ∗
   
   
    (
   
   
    1
   
   
    −
   
   
    S
   
   
    )
   
  
  
   I*(1-S)
  
 
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.68333em; vertical-align: 0em;"></span><span class="mord mathdefault" style="margin-right: 0.07847em;">I</span><span class="mspace" style="margin-right: 0.2222222222222222em;"></span><span class="mbin">∗</span><span class="mspace" style="margin-right: 0.2222222222222222em;"></span></span><span class="base"><span class="strut" style="height: 1em; vertical-align: -0.25em;"></span><span class="mopen">(</span><span class="mord">1</span><span class="mspace" style="margin-right: 0.2222222222222222em;"></span><span class="mbin">−</span><span class="mspace" style="margin-right: 0.2222222222222222em;"></span></span><span class="base"><span class="strut" style="height: 1em; vertical-align: -0.25em;"></span><span class="mord mathdefault" style="margin-right: 0.05764em;">S</span><span class="mclose">)</span></span></span></span></span>然后按照RGB的顺序接下面的公式就行了。<br data-filtered="filtered"> 我还特地设了个颜色好看一些～～记住结论算了，不记应该也没啥关系。</p>

2. HSI空间进行直方图均衡化

  因为考题里有这道题，查了半天，发现讲的实在少的可怜，还好找到了一篇硕士论文还有pitas在1996年发表的paper，于是也自己动手实践了一下，理解了。

问题：什么是HSI颜色模型，如何在HSI颜色空间保持图像色度(H)不变的情况下，对彩色图像做直方图均衡化处理

  实际上，对彩色图像做直方图均衡化有好多种思路，
  第一种人们都会想到的思路就是对直接抽取R、G、B的分量分别做一个直方图均衡化，然后就我的北登就可怜了，看下面的图在这里插入图片描述

可以看到这种方法会导致彩色色调的改变，所以事实上，这种方法并不是很推荐，但是运行起来的效率会非常的高。

Although the R G B space provides a straightforwardway to display color images, it is not always the best choice for processing and analysis. One of its disadvantages is its inability to handle the perceptual properties of colors, such as intensity, hue, or saturation. The H S I color space has primaries H (hue), S (saturation), and I (intensity) and corresponds directly to the perceptual attributes of colors

贴一段pitas的原话吧，这是他指出的在RGB空间直接做直方图均衡化的显著问题（自己翻译吧～-～）。
  第二种方法是pitas在1996年提出的，将图像先送入HSI空间我仅仅对S和I分量进行直方图处理或者仅仅对其做变化，事实上，我按pitas的方法做了一次有点小问题，毕竟每幅图不一样。
  HSI的值都是介于0-1之间的，然后pista提出了对 

    I
   
  
  
   I
  
 
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.68333em; vertical-align: 0em;"></span><span class="mord mathdefault" style="margin-right: 0.07847em;">I</span></span></span></span></span> 和 <span class="katex--inline"><span class="katex"><span class="katex-mathml">

 
  
   
    S
   
  
  
   S
  
 
</span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.68333em; vertical-align: 0em;"></span><span class="mord mathdefault" style="margin-right: 0.05764em;">S</span></span></span></span></span> 做处理的方法。</p>

  就是下面三个公式 

      f
     
     
      I
     
    
    
     (
    
    
     I
    
    
     )
    
    
     =
    
    
     
      {
     
     
      
       
        
         
          
           12
          
          
           
            I
           
           
            2
           
          
          
           
            哈
           
           
            哈
           
           
            哈
           
           
            哈
           
          
         
        
       
       
        
         
          
           for&nbsp;
          
          
           0
          
          
           ≤
          
          
           I
          
          
           ≤
          
          
           0.5
          
         
        
       
      
      
       
        
         
          
           12
          
          
           (
          
          
           1
          
          
           −
          
          
           I
          
          
           
            )
           
           
            2
           
          
          
           
            哈
           
           
            哈
           
           
            哈
           
          
         
        
       
       
        
         
          
           for&nbsp;
          
          
           0.5
          
          
           ≤
          
          
           I
          
          
           ≤
          
          
           1
          
         
        
       
      
     
    
   
   
    f_I(I) = <span class="MathJax_Preview" style="color: inherit; display: none;"></span><div class="MathJax_Display"><span class="MathJax MathJax_FullWidth" id="MathJax-Element-2-Frame" tabindex="0" style="position: relative;" data-mathml="<math xmlns=&quot;http://www.w3.org/1998/Math/MathML&quot; display=&quot;block&quot;><mrow><mo>{</mo><mtable columnalign=&quot;left left&quot; rowspacing=&quot;.2em&quot; columnspacing=&quot;1em&quot; displaystyle=&quot;false&quot;><mtr><mtd><mn>12</mn><msup><mi>I</mi><mn>2</mn></msup><mrow class=&quot;MJX-TeXAtom-ORD&quot;><mphantom><mrow class=&quot;MJX-TeXAtom-ORD&quot;><mo>&amp;#x54C8;</mo></mrow><mrow class=&quot;MJX-TeXAtom-ORD&quot;><mo>&amp;#x54C8;</mo></mrow><mrow class=&quot;MJX-TeXAtom-ORD&quot;><mo>&amp;#x54C8;</mo></mrow><mrow class=&quot;MJX-TeXAtom-ORD&quot;><mo>&amp;#x54C8;</mo></mrow></mphantom></mrow></mtd><mtd><mtext>for</mtext><mtext>&amp;#xA0;</mtext><mn>0</mn><mo>&amp;#x2264;</mo><mi>I</mi><mo>&amp;#x2264;</mo><mn>0.5</mn></mtd></mtr><mtr><mtd><mn>12</mn><mo stretchy=&quot;false&quot;>(</mo><mn>1</mn><mo>&amp;#x2212;</mo><mi>I</mi><msup><mo stretchy=&quot;false&quot;>)</mo><mn>2</mn></msup><mrow class=&quot;MJX-TeXAtom-ORD&quot;><mphantom><mrow class=&quot;MJX-TeXAtom-ORD&quot;><mo>&amp;#x54C8;</mo></mrow><mrow class=&quot;MJX-TeXAtom-ORD&quot;><mo>&amp;#x54C8;</mo></mrow><mrow class=&quot;MJX-TeXAtom-ORD&quot;><mo>&amp;#x54C8;</mo></mrow></mphantom></mrow></mtd><mtd><mtext>for</mtext><mtext>&amp;#xA0;</mtext><mn>0.5</mn><mo>&amp;#x2264;</mo><mi>I</mi><mo>&amp;#x2264;</mo><mn>1</mn></mtd></mtr></mtable><mo fence=&quot;true&quot; stretchy=&quot;true&quot; symmetric=&quot;true&quot;></mo></mrow></math>" role="presentation"><nobr aria-hidden="true"><span class="math" id="MathJax-Span-27" style="width: 100%; display: inline-block; min-width: 14.582em;"><span style="display: inline-block; position: relative; width: 100%; height: 0px; font-size: 102%;"><span style="position: absolute; clip: rect(2.382em, 1014.28em, 5.115em, -999.997em); top: -3.997em; left: 0em; width: 100%;"><span class="mrow" id="MathJax-Span-28"><span style="display: inline-block; position: relative; width: 100%; height: 0px;"><span style="position: absolute; clip: rect(2.382em, 1014.28em, 5.115em, -999.997em); top: -3.997em; left: 50%; margin-left: -7.135em;"><span class="mrow" id="MathJax-Span-29"><span class="mo" id="MathJax-Span-30" style="vertical-align: 0em;"><span style="font-family: MathJax_Size3;">{</span></span><span class="mtable" id="MathJax-Span-31" style="padding-right: 0.154em; padding-left: 0.154em;"><span style="display: inline-block; position: relative; width: 13.215em; height: 0px;"><span style="position: absolute; clip: rect(2.432em, 1004.41em, 5.065em, -999.997em); top: -3.997em; left: 0em;"><span style="display: inline-block; position: relative; width: 5.925em; height: 0px;"><span style="position: absolute; width: 100%; clip: rect(3.04em, 1002.03em, 4.356em, -999.997em); top: -4.554em; left: 0em;"><span class="mtd" id="MathJax-Span-32"><span class="mrow" id="MathJax-Span-33"><span style="display: inline-block; position: relative; width: 100%; height: 0px;"><span style="position: absolute; clip: rect(3.04em, 1002.03em, 4.356em, -999.997em); top: -3.997em; left: 50%; margin-left: -2.022em;"><span class="mn" id="MathJax-Span-34" style="font-family: MathJax_Main;">12</span><span class="msubsup" id="MathJax-Span-35"><span style="display: inline-block; position: relative; width: 1.015em; height: 0px;"><span style="position: absolute; clip: rect(3.192em, 1000.51em, 4.154em, -999.997em); top: -3.997em; left: 0em;"><span class="mi" id="MathJax-Span-36" style="font-family: MathJax_Math-italic;">I<span style="display: inline-block; overflow: hidden; height: 1px; width: 0.053em;"></span></span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span><span style="position: absolute; top: -4.351em; left: 0.559em;"><span class="mn" id="MathJax-Span-37" style="font-size: 70.7%; font-family: MathJax_Main;">2</span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span></span><span class="texatom" id="MathJax-Span-38"><span class="mrow" id="MathJax-Span-39"><span style="display: inline-block; position: relative; width: 2.027em; height: 0px;"><span style="position: absolute; clip: rect(3.04em, 1000em, 4.356em, -999.997em); top: -3.997em; left: 0em;"><span class="mphantom" id="MathJax-Span-40"><span class="mrow" id="MathJax-Span-41" style="visibility: hidden;"><span class="texatom" id="MathJax-Span-42"><span class="mrow" id="MathJax-Span-43"><span style="display: inline-block; position: relative; width: 0.509em; height: 0px;"><span style="position: absolute; clip: rect(3.04em, 1000.51em, 4.356em, -999.997em); top: -3.997em; left: 0em;"><span class="mo" id="MathJax-Span-44"><span style="font-family: STIXGeneral, &quot;Arial Unicode MS&quot;, serif; font-size: 98%; font-style: normal; font-weight: normal;">哈</span></span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span></span></span><span class="texatom" id="MathJax-Span-45"><span class="mrow" id="MathJax-Span-46"><span style="display: inline-block; position: relative; width: 0.509em; height: 0px;"><span style="position: absolute; clip: rect(3.04em, 1000.51em, 4.356em, -999.997em); top: -3.997em; left: 0em;"><span class="mo" id="MathJax-Span-47"><span style="font-family: STIXGeneral, &quot;Arial Unicode MS&quot;, serif; font-size: 98%; font-style: normal; font-weight: normal;">哈</span></span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span></span></span><span class="texatom" id="MathJax-Span-48"><span class="mrow" id="MathJax-Span-49"><span style="display: inline-block; position: relative; width: 0.509em; height: 0px;"><span style="position: absolute; clip: rect(3.04em, 1000.51em, 4.356em, -999.997em); top: -3.997em; left: 0em;"><span class="mo" id="MathJax-Span-50"><span style="font-family: STIXGeneral, &quot;Arial Unicode MS&quot;, serif; font-size: 98%; font-style: normal; font-weight: normal;">哈</span></span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span></span></span><span class="texatom" id="MathJax-Span-51"><span class="mrow" id="MathJax-Span-52"><span style="display: inline-block; position: relative; width: 0.509em; height: 0px;"><span style="position: absolute; clip: rect(3.04em, 1000.51em, 4.356em, -999.997em); top: -3.997em; left: 0em;"><span class="mo" id="MathJax-Span-53"><span style="font-family: STIXGeneral, &quot;Arial Unicode MS&quot;, serif; font-size: 98%; font-style: normal; font-weight: normal;">哈</span></span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span></span></span></span></span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span></span></span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span></span></span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span><span style="position: absolute; width: 100%; clip: rect(3.04em, 1004.41em, 4.407em, -999.997em); top: -3.339em; left: 0em;"><span class="mtd" id="MathJax-Span-63"><span class="mrow" id="MathJax-Span-64"><span style="display: inline-block; position: relative; width: 100%; height: 0px;"><span style="position: absolute; clip: rect(3.04em, 1004.41em, 4.407em, -999.997em); top: -3.997em; left: 50%; margin-left: -2.934em;"><span class="mn" id="MathJax-Span-65" style="font-family: MathJax_Main;">12</span><span class="mo" id="MathJax-Span-66" style="font-family: MathJax_Main;">(</span><span class="mn" id="MathJax-Span-67" style="font-family: MathJax_Main;">1</span><span class="mo" id="MathJax-Span-68" style="font-family: MathJax_Main; padding-left: 0.205em;">−</span><span class="mi" id="MathJax-Span-69" style="font-family: MathJax_Math-italic; padding-left: 0.205em;">I<span style="display: inline-block; overflow: hidden; height: 1px; width: 0.053em;"></span></span><span class="msubsup" id="MathJax-Span-70"><span style="display: inline-block; position: relative; width: 0.812em; height: 0px;"><span style="position: absolute; clip: rect(3.091em, 1000.31em, 4.407em, -999.997em); top: -3.997em; left: 0em;"><span class="mo" id="MathJax-Span-71" style="font-family: MathJax_Main;">)</span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span><span style="position: absolute; top: -4.351em; left: 0.408em;"><span class="mn" id="MathJax-Span-72" style="font-size: 70.7%; font-family: MathJax_Main;">2</span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span></span><span class="texatom" id="MathJax-Span-73"><span class="mrow" id="MathJax-Span-74"><span style="display: inline-block; position: relative; width: 1.521em; height: 0px;"><span style="position: absolute; clip: rect(3.04em, 1000em, 4.356em, -999.997em); top: -3.997em; left: 0em;"><span class="mphantom" id="MathJax-Span-75"><span class="mrow" id="MathJax-Span-76" style="visibility: hidden;"><span class="texatom" id="MathJax-Span-77"><span class="mrow" id="MathJax-Span-78"><span style="display: inline-block; position: relative; width: 0.509em; height: 0px;"><span style="position: absolute; clip: rect(3.04em, 1000.51em, 4.356em, -999.997em); top: -3.997em; left: 0em;"><span class="mo" id="MathJax-Span-79"><span style="font-family: STIXGeneral, &quot;Arial Unicode MS&quot;, serif; font-size: 98%; font-style: normal; font-weight: normal;">哈</span></span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span></span></span><span class="texatom" id="MathJax-Span-80"><span class="mrow" id="MathJax-Span-81"><span style="display: inline-block; position: relative; width: 0.509em; height: 0px;"><span style="position: absolute; clip: rect(3.04em, 1000.51em, 4.356em, -999.997em); top: -3.997em; left: 0em;"><span class="mo" id="MathJax-Span-82"><span style="font-family: STIXGeneral, &quot;Arial Unicode MS&quot;, serif; font-size: 98%; font-style: normal; font-weight: normal;">哈</span></span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span></span></span><span class="texatom" id="MathJax-Span-83"><span class="mrow" id="MathJax-Span-84"><span style="display: inline-block; position: relative; width: 0.509em; height: 0px;"><span style="position: absolute; clip: rect(3.04em, 1000.51em, 4.356em, -999.997em); top: -3.997em; left: 0em;"><span class="mo" id="MathJax-Span-85"><span style="font-family: STIXGeneral, &quot;Arial Unicode MS&quot;, serif; font-size: 98%; font-style: normal; font-weight: normal;">哈</span></span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span></span></span></span></span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span></span></span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span></span></span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span><span style="position: absolute; clip: rect(2.584em, 1006.28em, 4.964em, -999.997em); top: -3.997em; left: 6.887em;"><span style="display: inline-block; position: relative; width: 6.33em; height: 0px;"><span style="position: absolute; width: 100%; clip: rect(3.141em, 1006.28em, 4.305em, -999.997em); top: -4.554em; left: 0em;"><span class="mtd" id="MathJax-Span-54"><span class="mrow" id="MathJax-Span-55"><span style="display: inline-block; position: relative; width: 100%; height: 0px;"><span style="position: absolute; clip: rect(3.141em, 1006.28em, 4.305em, -999.997em); top: -3.997em; left: 50%; margin-left: -3.136em;"><span class="mtext" id="MathJax-Span-56" style="font-family: MathJax_Main;">for</span><span class="mtext" id="MathJax-Span-57" style="font-family: MathJax_Main;">&nbsp;</span><span class="mn" id="MathJax-Span-58" style="font-family: MathJax_Main;">0</span><span class="mo" id="MathJax-Span-59" style="font-family: MathJax_Main; padding-left: 0.256em;">≤</span><span class="mi" id="MathJax-Span-60" style="font-family: MathJax_Math-italic; padding-left: 0.256em;">I<span style="display: inline-block; overflow: hidden; height: 1px; width: 0.053em;"></span></span><span class="mo" id="MathJax-Span-61" style="font-family: MathJax_Main; padding-left: 0.256em;">≤</span><span class="mn" id="MathJax-Span-62" style="font-family: MathJax_Main; padding-left: 0.256em;">0.5</span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span></span></span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span><span style="position: absolute; width: 100%; clip: rect(3.141em, 1006.23em, 4.305em, -999.997em); top: -3.339em; left: 0em;"><span class="mtd" id="MathJax-Span-86"><span class="mrow" id="MathJax-Span-87"><span style="display: inline-block; position: relative; width: 100%; height: 0px;"><span style="position: absolute; clip: rect(3.141em, 1006.23em, 4.305em, -999.997em); top: -3.997em; left: 50%; margin-left: -3.136em;"><span class="mtext" id="MathJax-Span-88" style="font-family: MathJax_Main;">for</span><span class="mtext" id="MathJax-Span-89" style="font-family: MathJax_Main;">&nbsp;</span><span class="mn" id="MathJax-Span-90" style="font-family: MathJax_Main;">0.5</span><span class="mo" id="MathJax-Span-91" style="font-family: MathJax_Main; padding-left: 0.256em;">≤</span><span class="mi" id="MathJax-Span-92" style="font-family: MathJax_Math-italic; padding-left: 0.256em;">I<span style="display: inline-block; overflow: hidden; height: 1px; width: 0.053em;"></span></span><span class="mo" id="MathJax-Span-93" style="font-family: MathJax_Main; padding-left: 0.256em;">≤</span><span class="mn" id="MathJax-Span-94" style="font-family: MathJax_Main; padding-left: 0.256em;">1</span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span></span></span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span></span><span class="mo" id="MathJax-Span-95"></span></span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span></span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span><span style="display: inline-block; overflow: hidden; vertical-align: -1.03em; border-left: 0px solid; width: 0px; height: 2.533em;"></span></span></nobr><span class="MJX_Assistive_MathML MJX_Assistive_MathML_Block" role="presentation"><math xmlns="http://www.w3.org/1998/Math/MathML" display="block"><mrow><mo>{</mo><mtable columnalign="left left" rowspacing=".2em" columnspacing="1em" displaystyle="false"><mtr><mtd><mn>12</mn><msup><mi>I</mi><mn>2</mn></msup><mrow class="MJX-TeXAtom-ORD"><mphantom><mrow class="MJX-TeXAtom-ORD"><mo>哈</mo></mrow><mrow class="MJX-TeXAtom-ORD"><mo>哈</mo></mrow><mrow class="MJX-TeXAtom-ORD"><mo>哈</mo></mrow><mrow class="MJX-TeXAtom-ORD"><mo>哈</mo></mrow></mphantom></mrow></mtd><mtd><mtext>for</mtext><mtext>&nbsp;</mtext><mn>0</mn><mo>≤</mo><mi>I</mi><mo>≤</mo><mn>0.5</mn></mtd></mtr><mtr><mtd><mn>12</mn><mo stretchy="false">(</mo><mn>1</mn><mo>−</mo><mi>I</mi><msup><mo stretchy="false">)</mo><mn>2</mn></msup><mrow class="MJX-TeXAtom-ORD"><mphantom><mrow class="MJX-TeXAtom-ORD"><mo>哈</mo></mrow><mrow class="MJX-TeXAtom-ORD"><mo>哈</mo></mrow><mrow class="MJX-TeXAtom-ORD"><mo>哈</mo></mrow></mphantom></mrow></mtd><mtd><mtext>for</mtext><mtext>&nbsp;</mtext><mn>0.5</mn><mo>≤</mo><mi>I</mi><mo>≤</mo><mn>1</mn></mtd></mtr></mtable><mo fence="true" stretchy="true" symmetric="true"></mo></mrow></math></span></span></div><script type="math/tex; mode=display" id="MathJax-Element-2">begin{cases}12I^2 phantom{哈哈哈哈} & text{for}  0 le I le 0.5 \ 12(1-I)^2 phantom{哈哈哈} & text{for}  0.5 le I le 1 end{cases}</script>
   
  
 </span><span class="katex-html"><span class="base"><span class="strut" style="height: 1em; vertical-align: -0.25em;"></span><span class="mord"><span class="mord mathdefault" style="margin-right: 0.10764em;">f</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.32833099999999993em;"><span class="" style="top: -2.5500000000000003em; margin-left: -0.10764em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mathdefault mtight" style="margin-right: 0.07847em;">I</span></span></span></span><span class="vlist-s">​</span></span><span class="vlist-r"><span class="vlist" style="height: 0.15em;"><span class=""></span></span></span></span></span></span><span class="mopen">(</span><span class="mord mathdefault" style="margin-right: 0.07847em;">I</span><span class="mclose">)</span><span class="mspace" style="margin-right: 0.2777777777777778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right: 0.2777777777777778em;"></span></span><span class="base"><span class="strut" style="height: 3.0000299999999998em; vertical-align: -1.25003em;"></span><span class="minner"><span class="mopen delimcenter" style="top: 0em;"><span class="delimsizing size4">{<!-- --></span></span><span class="mord"><span class="mtable"><span class="col-align-l"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 1.69em;"><span class="" style="top: -3.69em;"><span class="pstrut" style="height: 3.008em;"></span><span class="mord"><span class="mord">1</span><span class="mord">2</span><span class="mord"><span class="mord mathdefault" style="margin-right: 0.07847em;">I</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.8141079999999999em;"><span class="" style="top: -3.063em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">2</span></span></span></span></span></span></span></span><span class="mord cjk_fallback" style="color: transparent;">哈</span><span class="mord cjk_fallback" style="color: transparent;">哈</span><span class="mord cjk_fallback" style="color: transparent;">哈</span><span class="mord cjk_fallback" style="color: transparent;">哈</span></span></span><span class="" style="top: -2.25em;"><span class="pstrut" style="height: 3.008em;"></span><span class="mord"><span class="mord">1</span><span class="mord">2</span><span class="mopen">(</span><span class="mord">1</span><span class="mspace" style="margin-right: 0.2222222222222222em;"></span><span class="mbin">−</span><span class="mspace" style="margin-right: 0.2222222222222222em;"></span><span class="mord mathdefault" style="margin-right: 0.07847em;">I</span><span class="mclose"><span class="mclose">)</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.8141079999999999em;"><span class="" style="top: -3.063em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">2</span></span></span></span></span></span></span></span><span class="mord cjk_fallback" style="color: transparent;">哈</span><span class="mord cjk_fallback" style="color: transparent;">哈</span><span class="mord cjk_fallback" style="color: transparent;">哈</span></span></span></span><span class="vlist-s">​</span></span><span class="vlist-r"><span class="vlist" style="height: 1.19em;"><span class=""></span></span></span></span></span><span class="arraycolsep" style="width: 1em;"></span><span class="col-align-l"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 1.69em;"><span class="" style="top: -3.69em;"><span class="pstrut" style="height: 3.008em;"></span><span class="mord"><span class="mord text"><span class="mord">for</span></span><span class="mspace">&nbsp;</span><span class="mord">0</span><span class="mspace" style="margin-right: 0.2777777777777778em;"></span><span class="mrel">≤</span><span class="mspace" style="margin-right: 0.2777777777777778em;"></span><span class="mord mathdefault" style="margin-right: 0.07847em;">I</span><span class="mspace" style="margin-right: 0.2777777777777778em;"></span><span class="mrel">≤</span><span class="mspace" style="margin-right: 0.2777777777777778em;"></span><span class="mord">0</span><span class="mord">.</span><span class="mord">5</span></span></span><span class="" style="top: -2.25em;"><span class="pstrut" style="height: 3.008em;"></span><span class="mord"><span class="mord text"><span class="mord">for</span></span><span class="mspace">&nbsp;</span><span class="mord">0</span><span class="mord">.</span><span class="mord">5</span><span class="mspace" style="margin-right: 0.2777777777777778em;"></span><span class="mrel">≤</span><span class="mspace" style="margin-right: 0.2777777777777778em;"></span><span class="mord mathdefault" style="margin-right: 0.07847em;">I</span><span class="mspace" style="margin-right: 0.2777777777777778em;"></span><span class="mrel">≤</span><span class="mspace" style="margin-right: 0.2777777777777778em;"></span><span class="mord">1</span></span></span></span><span class="vlist-s">​</span></span><span class="vlist-r"><span class="vlist" style="height: 1.19em;"><span class=""></span></span></span></span></span></span></span><span class="mclose nulldelimiter"></span></span></span></span></span></span></span></p>

这个是单独对 

     I
    
   
   
    I
   
  
 </span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.68333em; vertical-align: 0em;"></span><span class="mord mathdefault" style="margin-right: 0.07847em;">I</span></span></span></span></span> 进行处理的公式，根据范围来处理就可。</font><br data-filtered="filtered"> <span class="katex--display"><span class="katex-display"><span class="katex"><span class="katex-mathml">
 
  
   
    
     
      f
     
     
      s
     
    
    
     (
    
    
     S
    
    
     )
    
    
     =
    
    
     6
    
    
     S
    
    
     −
    
    
     6
    
    
     
      S
     
     
      2
     
    
    
     
      哈
     
     
      哈
     
     
      哈
     
     
      哈
     
     
      哈
     
    
    
     for&nbsp;
    
    
     0
    
    
     ≤
    
    
     S
    
    
     ≤
    
    
     1
    
   
   
    f_s(S) = 6S - 6S^2 phantom{哈哈哈哈哈} text{for}  0 le S le 1 
   
  
 </span><span class="katex-html"><span class="base"><span class="strut" style="height: 1em; vertical-align: -0.25em;"></span><span class="mord"><span class="mord mathdefault" style="margin-right: 0.10764em;">f</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.151392em;"><span class="" style="top: -2.5500000000000003em; margin-left: -0.10764em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mathdefault mtight">s</span></span></span></span><span class="vlist-s">​</span></span><span class="vlist-r"><span class="vlist" style="height: 0.15em;"><span class=""></span></span></span></span></span></span><span class="mopen">(</span><span class="mord mathdefault" style="margin-right: 0.05764em;">S</span><span class="mclose">)</span><span class="mspace" style="margin-right: 0.2777777777777778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right: 0.2777777777777778em;"></span></span><span class="base"><span class="strut" style="height: 0.76666em; vertical-align: -0.08333em;"></span><span class="mord">6</span><span class="mord mathdefault" style="margin-right: 0.05764em;">S</span><span class="mspace" style="margin-right: 0.2222222222222222em;"></span><span class="mbin">−</span><span class="mspace" style="margin-right: 0.2222222222222222em;"></span></span><span class="base"><span class="strut" style="height: 1.0000779999999998em; vertical-align: -0.13597em;"></span><span class="mord">6</span><span class="mord"><span class="mord mathdefault" style="margin-right: 0.05764em;">S</span><span class="msupsub"><span class="vlist-t"><span class="vlist-r"><span class="vlist" style="height: 0.8641079999999999em;"><span class="" style="top: -3.113em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight">2</span></span></span></span></span></span></span></span><span class="mord cjk_fallback" style="color: transparent;">哈</span><span class="mord cjk_fallback" style="color: transparent;">哈</span><span class="mord cjk_fallback" style="color: transparent;">哈</span><span class="mord cjk_fallback" style="color: transparent;">哈</span><span class="mord cjk_fallback" style="color: transparent;">哈</span><span class="mord text"><span class="mord">for</span></span><span class="mspace">&nbsp;</span><span class="mord">0</span><span class="mspace" style="margin-right: 0.2777777777777778em;"></span><span class="mrel">≤</span><span class="mspace" style="margin-right: 0.2777777777777778em;"></span></span><span class="base"><span class="strut" style="height: 0.8193em; vertical-align: -0.13597em;"></span><span class="mord mathdefault" style="margin-right: 0.05764em;">S</span><span class="mspace" style="margin-right: 0.2777777777777778em;"></span><span class="mrel">≤</span><span class="mspace" style="margin-right: 0.2777777777777778em;"></span></span><span class="base"><span class="strut" style="height: 0.64444em; vertical-align: 0em;"></span><span class="mord">1</span></span></span></span></span></span><font color="blue">这个是单独对 <span class="katex--inline"><span class="katex"><span class="katex-mathml">
 
  
   
    
     S
    
   
   
    S
   
  
 </span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.68333em; vertical-align: 0em;"></span><span class="mord mathdefault" style="margin-right: 0.05764em;">S</span></span></span></span></span> 进行处理的公式，根据范围来处理就可。</font></p> 


      f
     
     
      
       I
      
      
       S
      
     
    
    
     (
    
    
     I
    
    
     ,
    
    
     S
    
    
     )
    
    
     =
    
    
     
      {
     
     
      
       
        
         
          
           6
          
          
           S
          
          
           
            哈
           
           
            哈
           
          
         
        
       
       
        
         
          
           for&nbsp;
          
          
           S
          
          
           ≤
          
          
           2
          
          
           I
          
          
           ,
          
          
           I
          
          
           ∈
          
          
           [
          
          
           0
          
          
           ,
          
          
           
            1
           
           
            2
           
          
          
           ]
          
         
        
       
      
      
       
        
         
          0
         
        
       
       
        
         
          
           for&nbsp;
          
          
           S
          
          
           &gt;
          
          
           2
          
          
           I
          
          
           ,
          
          
           ∈
          
          
           [
          
          
           0
          
          
           ,
          
          
           
            1
           
           
            2
           
          
          
           ]
          
         
        
       
      
      
       
        
         
          
           6
          
          
           S
          
         
        
       
       
        
         
          
           for&nbsp;
          
          
           S
          
          
           ≤
          
          
           2
          
          
           (
          
          
           1
          
          
           −
          
          
           I
          
          
           )
          
          
           ,
          
          
           I
          
          
           ∈
          
          
           [
          
          
           
            1
           
           
            2
           
          
          
           ,
          
          
           1
          
          
           ]
          
         
        
       
      
      
       
        
         
          0
         
        
       
       
        
         
          
           for&nbsp;
          
          
           S
          
          
           &gt;
          
          
           2
          
          
           (
          
          
           1
          
          
           −
          
          
           I
          
          
           )
          
          
           ,
          
          
           I
          
          
           ∈
          
          
           [
          
          
           
            1
           
           
            2
           
          
          
           ,
          
          
           1
          
          
           ]
          
         
        
       
      
     
    
   
   
    f_{IS}(I,S) = <span class="MathJax_Preview" style="color: inherit; display: none;"></span><div class="MathJax_Display"><span class="MathJax MathJax_FullWidth" id="MathJax-Element-3-Frame" tabindex="0" data-mathml="<math xmlns=&quot;http://www.w3.org/1998/Math/MathML&quot; display=&quot;block&quot;><mrow><mo>{</mo><mtable columnalign=&quot;left left&quot; rowspacing=&quot;.2em&quot; columnspacing=&quot;1em&quot; displaystyle=&quot;false&quot;><mtr><mtd><mn>6</mn><mi>S</mi><mrow class=&quot;MJX-TeXAtom-ORD&quot;><mphantom><mrow class=&quot;MJX-TeXAtom-ORD&quot;><mo>&amp;#x54C8;</mo></mrow><mrow class=&quot;MJX-TeXAtom-ORD&quot;><mo>&amp;#x54C8;</mo></mrow></mphantom></mrow></mtd><mtd><mtext>for</mtext><mtext>&amp;#xA0;</mtext><mi>S</mi><mo>&amp;#x2264;</mo><mn>2</mn><mi>I</mi><mo>,</mo><mi>I</mi><mo>&amp;#x2208;</mo><mo stretchy=&quot;false&quot;>[</mo><mn>0</mn><mo>,</mo><mfrac><mn>1</mn><mn>2</mn></mfrac><mo stretchy=&quot;false&quot;>]</mo></mtd></mtr><mtr><mtd><mn>0</mn></mtd><mtd><mtext>for</mtext><mtext>&amp;#xA0;</mtext><mi>S</mi><mo>&amp;#x003E;</mo><mn>2</mn><mi>I</mi><mo>,</mo><mo>&amp;#x2208;</mo><mo stretchy=&quot;false&quot;>[</mo><mn>0</mn><mo>,</mo><mfrac><mn>1</mn><mn>2</mn></mfrac><mo stretchy=&quot;false&quot;>]</mo></mtd></mtr><mtr><mtd><mn>6</mn><mi>S</mi></mtd><mtd><mtext>for</mtext><mtext>&amp;#xA0;</mtext><mi>S</mi><mo>&amp;#x2264;</mo><mn>2</mn><mo stretchy=&quot;false&quot;>(</mo><mn>1</mn><mo>&amp;#x2212;</mo><mi>I</mi><mo stretchy=&quot;false&quot;>)</mo><mo>,</mo><mi>I</mi><mo>&amp;#x2208;</mo><mo stretchy=&quot;false&quot;>[</mo><mfrac><mn>1</mn><mn>2</mn></mfrac><mo>,</mo><mn>1</mn><mo stretchy=&quot;false&quot;>]</mo></mtd></mtr><mtr><mtd><mn>0</mn></mtd><mtd><mtext>for</mtext><mtext>&amp;#xA0;</mtext><mi>S</mi><mo>&amp;#x003E;</mo><mn>2</mn><mo stretchy=&quot;false&quot;>(</mo><mn>1</mn><mo>&amp;#x2212;</mo><mi>I</mi><mo stretchy=&quot;false&quot;>)</mo><mo>,</mo><mi>I</mi><mo>&amp;#x2208;</mo><mo stretchy=&quot;false&quot;>[</mo><mfrac><mn>1</mn><mn>2</mn></mfrac><mo>,</mo><mn>1</mn><mo stretchy=&quot;false&quot;>]</mo></mtd></mtr></mtable><mo fence=&quot;true&quot; stretchy=&quot;true&quot; symmetric=&quot;true&quot;></mo></mrow></math>" role="presentation" style="position: relative;"><nobr aria-hidden="true"><span class="math" id="MathJax-Span-96" style="width: 100%; display: inline-block; min-width: 15.797em;"><span style="display: inline-block; position: relative; width: 100%; height: 0px; font-size: 102%;"><span style="position: absolute; clip: rect(3.445em, 1015.49em, 9.317em, -999.997em); top: -6.629em; left: 0em; width: 100%;"><span class="mrow" id="MathJax-Span-97"><span style="display: inline-block; position: relative; width: 100%; height: 0px;"><span style="position: absolute; clip: rect(3.445em, 1015.49em, 9.317em, -999.997em); top: -6.629em; left: 50%; margin-left: -7.743em;"><span class="mrow" id="MathJax-Span-98"><span class="mo" id="MathJax-Span-99" style="vertical-align: 3.04em;"><span style="display: inline-block; position: relative; width: 0.914em; height: 0px;"><span style="position: absolute; font-family: MathJax_Size4; top: -3.085em; left: 0em;">⎧<span style="display: inline-block; width: 0px; height: 4.002em;"></span></span><span style="position: absolute; font-family: MathJax_Size4; top: 0.711em; left: 0em;">⎩<span style="display: inline-block; width: 0px; height: 4.002em;"></span></span><span style="position: absolute; font-family: MathJax_Size4; top: -0.959em; left: 0em;">⎨<span style="display: inline-block; width: 0px; height: 4.002em;"></span></span><span style="font-family: MathJax_Size4; position: absolute; top: -2.832em; left: 0em;">⎪<span style="display: inline-block; width: 0px; height: 4.002em;"></span></span><span style="font-family: MathJax_Size4; position: absolute; top: -2.579em; left: 0em;">⎪<span style="display: inline-block; width: 0px; height: 4.002em;"></span></span><span style="font-family: MathJax_Size4; position: absolute; top: -2.326em; left: 0em;">⎪<span style="display: inline-block; width: 0px; height: 4.002em;"></span></span><span style="font-family: MathJax_Size4; position: absolute; top: -2.073em; left: 0em;">⎪<span style="display: inline-block; width: 0px; height: 4.002em;"></span></span><span style="font-family: MathJax_Size4; position: absolute; top: -0.048em; left: 0em;">⎪<span style="display: inline-block; width: 0px; height: 4.002em;"></span></span><span style="font-family: MathJax_Size4; position: absolute; top: 0.205em; left: 0em;">⎪<span style="display: inline-block; width: 0px; height: 4.002em;"></span></span><span style="font-family: MathJax_Size4; position: absolute; top: 0.509em; left: 0em;">⎪<span style="display: inline-block; width: 0px; height: 4.002em;"></span></span><span style="font-family: MathJax_Size4; position: absolute; top: 0.762em; left: 0em;">⎪<span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span></span><span class="mtable" id="MathJax-Span-100" style="padding-right: 0.154em; padding-left: 0.154em;"><span style="display: inline-block; position: relative; width: 14.329em; height: 0px;"><span style="position: absolute; clip: rect(3.04em, 1001.17em, 8.507em, -999.997em); top: -6.173em; left: 0em;"><span style="display: inline-block; position: relative; width: 2.129em; height: 0px;"><span style="position: absolute; width: 100%; clip: rect(3.04em, 1001.17em, 4.356em, -999.997em); top: -6.173em; left: 0em;"><span class="mtd" id="MathJax-Span-101"><span class="mrow" id="MathJax-Span-102"><span style="display: inline-block; position: relative; width: 100%; height: 0px;"><span style="position: absolute; clip: rect(3.04em, 1001.17em, 4.356em, -999.997em); top: -3.997em; left: 50%; margin-left: -1.061em;"><span class="mn" id="MathJax-Span-103" style="font-family: MathJax_Main;">6</span><span class="mi" id="MathJax-Span-104" style="font-family: MathJax_Math-italic;">S<span style="display: inline-block; overflow: hidden; height: 1px; width: 0.053em;"></span></span><span class="texatom" id="MathJax-Span-105"><span class="mrow" id="MathJax-Span-106"><span style="display: inline-block; position: relative; width: 1.015em; height: 0px;"><span style="position: absolute; clip: rect(3.04em, 1000em, 4.356em, -999.997em); top: -3.997em; left: 0em;"><span class="mphantom" id="MathJax-Span-107"><span class="mrow" id="MathJax-Span-108" style="visibility: hidden;"><span class="texatom" id="MathJax-Span-109"><span class="mrow" id="MathJax-Span-110"><span style="display: inline-block; position: relative; width: 0.509em; height: 0px;"><span style="position: absolute; clip: rect(3.04em, 1000.51em, 4.356em, -999.997em); top: -3.997em; left: 0em;"><span class="mo" id="MathJax-Span-111"><span style="font-family: STIXGeneral, &quot;Arial Unicode MS&quot;, serif; font-size: 98%; font-style: normal; font-weight: normal;">哈</span></span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span></span></span><span class="texatom" id="MathJax-Span-112"><span class="mrow" id="MathJax-Span-113"><span style="display: inline-block; position: relative; width: 0.509em; height: 0px;"><span style="position: absolute; clip: rect(3.04em, 1000.51em, 4.356em, -999.997em); top: -3.997em; left: 0em;"><span class="mo" id="MathJax-Span-114"><span style="font-family: STIXGeneral, &quot;Arial Unicode MS&quot;, serif; font-size: 98%; font-style: normal; font-weight: normal;">哈</span></span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span></span></span></span></span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span></span></span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span></span></span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span><span style="position: absolute; width: 100%; clip: rect(3.192em, 1000.46em, 4.154em, -999.997em); top: -4.705em; left: 0em;"><span class="mtd" id="MathJax-Span-133"><span class="mrow" id="MathJax-Span-134"><span style="display: inline-block; position: relative; width: 100%; height: 0px;"><span style="position: absolute; clip: rect(3.192em, 1000.46em, 4.154em, -999.997em); top: -3.997em; left: 50%; margin-left: -0.251em;"><span class="mn" id="MathJax-Span-135" style="font-family: MathJax_Main;">0</span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span></span></span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span><span style="position: absolute; width: 100%; clip: rect(3.141em, 1001.17em, 4.154em, -999.997em); top: -3.288em; left: 0em;"><span class="mtd" id="MathJax-Span-153"><span class="mrow" id="MathJax-Span-154"><span style="display: inline-block; position: relative; width: 100%; height: 0px;"><span style="position: absolute; clip: rect(3.141em, 1001.17em, 4.154em, -999.997em); top: -3.997em; left: 50%; margin-left: -0.554em;"><span class="mn" id="MathJax-Span-155" style="font-family: MathJax_Main;">6</span><span class="mi" id="MathJax-Span-156" style="font-family: MathJax_Math-italic;">S<span style="display: inline-block; overflow: hidden; height: 1px; width: 0.053em;"></span></span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span></span></span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span><span style="position: absolute; width: 100%; clip: rect(3.192em, 1000.46em, 4.154em, -999.997em); top: -1.82em; left: 0em;"><span class="mtd" id="MathJax-Span-179"><span class="mrow" id="MathJax-Span-180"><span style="display: inline-block; position: relative; width: 100%; height: 0px;"><span style="position: absolute; clip: rect(3.192em, 1000.46em, 4.154em, -999.997em); top: -3.997em; left: 50%; margin-left: -0.251em;"><span class="mn" id="MathJax-Span-181" style="font-family: MathJax_Main;">0</span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span></span></span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span><span style="display: inline-block; width: 0px; height: 6.178em;"></span></span><span style="position: absolute; clip: rect(3.445em, 1011.04em, 9.317em, -999.997em); top: -6.629em; left: 3.141em;"><span style="display: inline-block; position: relative; width: 11.19em; height: 0px;"><span style="position: absolute; width: 100%; clip: rect(2.989em, 1008.61em, 4.508em, -999.997em); top: -6.173em; left: 0em;"><span class="mtd" id="MathJax-Span-115"><span class="mrow" id="MathJax-Span-116"><span style="display: inline-block; position: relative; width: 100%; height: 0px;"><span style="position: absolute; clip: rect(2.989em, 1008.61em, 4.508em, -999.997em); top: -3.997em; left: 50%; margin-left: -4.351em;"><span class="mtext" id="MathJax-Span-117" style="font-family: MathJax_Main;">for</span><span class="mtext" id="MathJax-Span-118" style="font-family: MathJax_Main;">&nbsp;</span><span class="mi" id="MathJax-Span-119" style="font-family: MathJax_Math-italic;">S<span style="display: inline-block; overflow: hidden; height: 1px; width: 0.053em;"></span></span><span class="mo" id="MathJax-Span-120" style="font-family: MathJax_Main; padding-left: 0.256em;">≤</span><span class="mn" id="MathJax-Span-121" style="font-family: MathJax_Main; padding-left: 0.256em;">2</span><span class="mi" id="MathJax-Span-122" style="font-family: MathJax_Math-italic;">I<span style="display: inline-block; overflow: hidden; height: 1px; width: 0.053em;"></span></span><span class="mo" id="MathJax-Span-123" style="font-family: MathJax_Main;">,</span><span class="mi" id="MathJax-Span-124" style="font-family: MathJax_Math-italic; padding-left: 0.154em;">I<span style="display: inline-block; overflow: hidden; height: 1px; width: 0.053em;"></span></span><span class="mo" id="MathJax-Span-125" style="font-family: MathJax_Main; padding-left: 0.256em;">∈</span><span class="mo" id="MathJax-Span-126" style="font-family: MathJax_Main; padding-left: 0.256em;">[</span><span class="mn" id="MathJax-Span-127" style="font-family: MathJax_Main;">0</span><span class="mo" id="MathJax-Span-128" style="font-family: MathJax_Main;">,</span><span class="mfrac" id="MathJax-Span-129" style="padding-left: 0.154em;"><span style="display: inline-block; position: relative; width: 0.458em; height: 0px; margin-right: 0.104em; margin-left: 0.104em;"><span style="position: absolute; clip: rect(3.394em, 1000.31em, 4.154em, -999.997em); top: -4.402em; left: 50%; margin-left: -0.149em;"><span class="mn" id="MathJax-Span-130" style="font-size: 70.7%; font-family: MathJax_Main;">1</span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span><span style="position: absolute; clip: rect(3.394em, 1000.31em, 4.154em, -999.997em); top: -3.642em; left: 50%; margin-left: -0.149em;"><span class="mn" id="MathJax-Span-131" style="font-size: 70.7%; font-family: MathJax_Main;">2</span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span><span style="position: absolute; clip: rect(0.863em, 1000.46em, 1.217em, -999.997em); top: -1.263em; left: 0em;"><span style="display: inline-block; overflow: hidden; vertical-align: 0em; border-top: 1.3px solid; width: 0.458em; height: 0px;"></span><span style="display: inline-block; width: 0px; height: 1.066em;"></span></span></span></span><span class="mo" id="MathJax-Span-132" style="font-family: MathJax_Main;">]</span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span></span></span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span><span style="position: absolute; width: 100%; clip: rect(2.989em, 1007.85em, 4.508em, -999.997em); top: -4.705em; left: 0em;"><span class="mtd" id="MathJax-Span-136"><span class="mrow" id="MathJax-Span-137"><span style="display: inline-block; position: relative; width: 100%; height: 0px;"><span style="position: absolute; clip: rect(2.989em, 1007.85em, 4.508em, -999.997em); top: -3.997em; left: 50%; margin-left: -3.946em;"><span class="mtext" id="MathJax-Span-138" style="font-family: MathJax_Main;">for</span><span class="mtext" id="MathJax-Span-139" style="font-family: MathJax_Main;">&nbsp;</span><span class="mi" id="MathJax-Span-140" style="font-family: MathJax_Math-italic;">S<span style="display: inline-block; overflow: hidden; height: 1px; width: 0.053em;"></span></span><span class="mo" id="MathJax-Span-141" style="font-family: MathJax_Main; padding-left: 0.256em;">&gt;</span><span class="mn" id="MathJax-Span-142" style="font-family: MathJax_Main; padding-left: 0.256em;">2</span><span class="mi" id="MathJax-Span-143" style="font-family: MathJax_Math-italic;">I<span style="display: inline-block; overflow: hidden; height: 1px; width: 0.053em;"></span></span><span class="mo" id="MathJax-Span-144" style="font-family: MathJax_Main;">,</span><span class="mo" id="MathJax-Span-145" style="font-family: MathJax_Main; padding-left: 0.154em;">∈</span><span class="mo" id="MathJax-Span-146" style="font-family: MathJax_Main; padding-left: 0.256em;">[</span><span class="mn" id="MathJax-Span-147" style="font-family: MathJax_Main;">0</span><span class="mo" id="MathJax-Span-148" style="font-family: MathJax_Main;">,</span><span class="mfrac" id="MathJax-Span-149" style="padding-left: 0.154em;"><span style="display: inline-block; position: relative; width: 0.458em; height: 0px; margin-right: 0.104em; margin-left: 0.104em;"><span style="position: absolute; clip: rect(3.394em, 1000.31em, 4.154em, -999.997em); top: -4.402em; left: 50%; margin-left: -0.149em;"><span class="mn" id="MathJax-Span-150" style="font-size: 70.7%; font-family: MathJax_Main;">1</span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span><span style="position: absolute; clip: rect(3.394em, 1000.31em, 4.154em, -999.997em); top: -3.642em; left: 50%; margin-left: -0.149em;"><span class="mn" id="MathJax-Span-151" style="font-size: 70.7%; font-family: MathJax_Main;">2</span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span><span style="position: absolute; clip: rect(0.863em, 1000.46em, 1.217em, -999.997em); top: -1.263em; left: 0em;"><span style="display: inline-block; overflow: hidden; vertical-align: 0em; border-top: 1.3px solid; width: 0.458em; height: 0px;"></span><span style="display: inline-block; width: 0px; height: 1.066em;"></span></span></span></span><span class="mo" id="MathJax-Span-152" style="font-family: MathJax_Main;">]</span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span></span></span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span><span style="position: absolute; width: 100%; clip: rect(2.989em, 1011.04em, 4.508em, -999.997em); top: -3.288em; left: 0em;"><span class="mtd" id="MathJax-Span-157"><span class="mrow" id="MathJax-Span-158"><span style="display: inline-block; position: relative; width: 100%; height: 0px;"><span style="position: absolute; clip: rect(2.989em, 1011.04em, 4.508em, -999.997em); top: -3.997em; left: 50%; margin-left: -5.566em;"><span class="mtext" id="MathJax-Span-159" style="font-family: MathJax_Main;">for</span><span class="mtext" id="MathJax-Span-160" style="font-family: MathJax_Main;">&nbsp;</span><span class="mi" id="MathJax-Span-161" style="font-family: MathJax_Math-italic;">S<span style="display: inline-block; overflow: hidden; height: 1px; width: 0.053em;"></span></span><span class="mo" id="MathJax-Span-162" style="font-family: MathJax_Main; padding-left: 0.256em;">≤</span><span class="mn" id="MathJax-Span-163" style="font-family: MathJax_Main; padding-left: 0.256em;">2</span><span class="mo" id="MathJax-Span-164" style="font-family: MathJax_Main;">(</span><span class="mn" id="MathJax-Span-165" style="font-family: MathJax_Main;">1</span><span class="mo" id="MathJax-Span-166" style="font-family: MathJax_Main; padding-left: 0.205em;">−</span><span class="mi" id="MathJax-Span-167" style="font-family: MathJax_Math-italic; padding-left: 0.205em;">I<span style="display: inline-block; overflow: hidden; height: 1px; width: 0.053em;"></span></span><span class="mo" id="MathJax-Span-168" style="font-family: MathJax_Main;">)</span><span class="mo" id="MathJax-Span-169" style="font-family: MathJax_Main;">,</span><span class="mi" id="MathJax-Span-170" style="font-family: MathJax_Math-italic; padding-left: 0.154em;">I<span style="display: inline-block; overflow: hidden; height: 1px; width: 0.053em;"></span></span><span class="mo" id="MathJax-Span-171" style="font-family: MathJax_Main; padding-left: 0.256em;">∈</span><span class="mo" id="MathJax-Span-172" style="font-family: MathJax_Main; padding-left: 0.256em;">[</span><span class="mfrac" id="MathJax-Span-173"><span style="display: inline-block; position: relative; width: 0.458em; height: 0px; margin-right: 0.104em; margin-left: 0.104em;"><span style="position: absolute; clip: rect(3.394em, 1000.31em, 4.154em, -999.997em); top: -4.402em; left: 50%; margin-left: -0.149em;"><span class="mn" id="MathJax-Span-174" style="font-size: 70.7%; font-family: MathJax_Main;">1</span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span><span style="position: absolute; clip: rect(3.394em, 1000.31em, 4.154em, -999.997em); top: -3.642em; left: 50%; margin-left: -0.149em;"><span class="mn" id="MathJax-Span-175" style="font-size: 70.7%; font-family: MathJax_Main;">2</span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span><span style="position: absolute; clip: rect(0.863em, 1000.46em, 1.217em, -999.997em); top: -1.263em; left: 0em;"><span style="display: inline-block; overflow: hidden; vertical-align: 0em; border-top: 1.3px solid; width: 0.458em; height: 0px;"></span><span style="display: inline-block; width: 0px; height: 1.066em;"></span></span></span></span><span class="mo" id="MathJax-Span-176" style="font-family: MathJax_Main;">,</span><span class="mn" id="MathJax-Span-177" style="font-family: MathJax_Main; padding-left: 0.154em;">1</span><span class="mo" id="MathJax-Span-178" style="font-family: MathJax_Main;">]</span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span></span></span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span><span style="position: absolute; width: 100%; clip: rect(2.989em, 1011.04em, 4.508em, -999.997em); top: -1.82em; left: 0em;"><span class="mtd" id="MathJax-Span-182"><span class="mrow" id="MathJax-Span-183"><span style="display: inline-block; position: relative; width: 100%; height: 0px;"><span style="position: absolute; clip: rect(2.989em, 1011.04em, 4.508em, -999.997em); top: -3.997em; left: 50%; margin-left: -5.566em;"><span class="mtext" id="MathJax-Span-184" style="font-family: MathJax_Main;">for</span><span class="mtext" id="MathJax-Span-185" style="font-family: MathJax_Main;">&nbsp;</span><span class="mi" id="MathJax-Span-186" style="font-family: MathJax_Math-italic;">S<span style="display: inline-block; overflow: hidden; height: 1px; width: 0.053em;"></span></span><span class="mo" id="MathJax-Span-187" style="font-family: MathJax_Main; padding-left: 0.256em;">&gt;</span><span class="mn" id="MathJax-Span-188" style="font-family: MathJax_Main; padding-left: 0.256em;">2</span><span class="mo" id="MathJax-Span-189" style="font-family: MathJax_Main;">(</span><span class="mn" id="MathJax-Span-190" style="font-family: MathJax_Main;">1</span><span class="mo" id="MathJax-Span-191" style="font-family: MathJax_Main; padding-left: 0.205em;">−</span><span class="mi" id="MathJax-Span-192" style="font-family: MathJax_Math-italic; padding-left: 0.205em;">I<span style="display: inline-block; overflow: hidden; height: 1px; width: 0.053em;"></span></span><span class="mo" id="MathJax-Span-193" style="font-family: MathJax_Main;">)</span><span class="mo" id="MathJax-Span-194" style="font-family: MathJax_Main;">,</span><span class="mi" id="MathJax-Span-195" style="font-family: MathJax_Math-italic; padding-left: 0.154em;">I<span style="display: inline-block; overflow: hidden; height: 1px; width: 0.053em;"></span></span><span class="mo" id="MathJax-Span-196" style="font-family: MathJax_Main; padding-left: 0.256em;">∈</span><span class="mo" id="MathJax-Span-197" style="font-family: MathJax_Main; padding-left: 0.256em;">[</span><span class="mfrac" id="MathJax-Span-198"><span style="display: inline-block; position: relative; width: 0.458em; height: 0px; margin-right: 0.104em; margin-left: 0.104em;"><span style="position: absolute; clip: rect(3.394em, 1000.31em, 4.154em, -999.997em); top: -4.402em; left: 50%; margin-left: -0.149em;"><span class="mn" id="MathJax-Span-199" style="font-size: 70.7%; font-family: MathJax_Main;">1</span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span><span style="position: absolute; clip: rect(3.394em, 1000.31em, 4.154em, -999.997em); top: -3.642em; left: 50%; margin-left: -0.149em;"><span class="mn" id="MathJax-Span-200" style="font-size: 70.7%; font-family: MathJax_Main;">2</span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span><span style="position: absolute; clip: rect(0.863em, 1000.46em, 1.217em, -999.997em); top: -1.263em; left: 0em;"><span style="display: inline-block; overflow: hidden; vertical-align: 0em; border-top: 1.3px solid; width: 0.458em; height: 0px;"></span><span style="display: inline-block; width: 0px; height: 1.066em;"></span></span></span></span><span class="mo" id="MathJax-Span-201" style="font-family: MathJax_Main;">,</span><span class="mn" id="MathJax-Span-202" style="font-family: MathJax_Main; padding-left: 0.154em;">1</span><span class="mo" id="MathJax-Span-203" style="font-family: MathJax_Main;">]</span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span></span></span><span style="display: inline-block; width: 0px; height: 4.002em;"></span></span></span><span style="display: inline-block; width: 0px; height: 6.634em;"></span></span></span></span><span class="mo" id="MathJax-Span-204"></span></span><span style="display: inline-block; width: 0px; height: 6.634em;"></span></span></span></span><span style="display: inline-block; width: 0px; height: 6.634em;"></span></span></span><span style="display: inline-block; overflow: hidden; vertical-align: -2.631em; border-left: 0px solid; width: 0px; height: 5.837em;"></span></span></nobr><span class="MJX_Assistive_MathML MJX_Assistive_MathML_Block" role="presentation"><math xmlns="http://www.w3.org/1998/Math/MathML" display="block"><mrow><mo>{</mo><mtable columnalign="left left" rowspacing=".2em" columnspacing="1em" displaystyle="false"><mtr><mtd><mn>6</mn><mi>S</mi><mrow class="MJX-TeXAtom-ORD"><mphantom><mrow class="MJX-TeXAtom-ORD"><mo>哈</mo></mrow><mrow class="MJX-TeXAtom-ORD"><mo>哈</mo></mrow></mphantom></mrow></mtd><mtd><mtext>for</mtext><mtext>&nbsp;</mtext><mi>S</mi><mo>≤</mo><mn>2</mn><mi>I</mi><mo>,</mo><mi>I</mi><mo>∈</mo><mo stretchy="false">[</mo><mn>0</mn><mo>,</mo><mfrac><mn>1</mn><mn>2</mn></mfrac><mo stretchy="false">]</mo></mtd></mtr><mtr><mtd><mn>0</mn></mtd><mtd><mtext>for</mtext><mtext>&nbsp;</mtext><mi>S</mi><mo>&gt;</mo><mn>2</mn><mi>I</mi><mo>,</mo><mo>∈</mo><mo stretchy="false">[</mo><mn>0</mn><mo>,</mo><mfrac><mn>1</mn><mn>2</mn></mfrac><mo stretchy="false">]</mo></mtd></mtr><mtr><mtd><mn>6</mn><mi>S</mi></mtd><mtd><mtext>for</mtext><mtext>&nbsp;</mtext><mi>S</mi><mo>≤</mo><mn>2</mn><mo stretchy="false">(</mo><mn>1</mn><mo>−</mo><mi>I</mi><mo stretchy="false">)</mo><mo>,</mo><mi>I</mi><mo>∈</mo><mo stretchy="false">[</mo><mfrac><mn>1</mn><mn>2</mn></mfrac><mo>,</mo><mn>1</mn><mo stretchy="false">]</mo></mtd></mtr><mtr><mtd><mn>0</mn></mtd><mtd><mtext>for</mtext><mtext>&nbsp;</mtext><mi>S</mi><mo>&gt;</mo><mn>2</mn><mo stretchy="false">(</mo><mn>1</mn><mo>−</mo><mi>I</mi><mo stretchy="false">)</mo><mo>,</mo><mi>I</mi><mo>∈</mo><mo stretchy="false">[</mo><mfrac><mn>1</mn><mn>2</mn></mfrac><mo>,</mo><mn>1</mn><mo stretchy="false">]</mo></mtd></mtr></mtable><mo fence="true" stretchy="true" symmetric="true"></mo></mrow></math></span></span></div><script type="math/tex; mode=display" id="MathJax-Element-3">begin{cases} 6S phantom{哈哈} &text{for}  S le2I, I in[0,frac{1}{2}] \ 0 & text{for}  S gt 2I, in[0,frac{1}{2}] \ 6S & text{for}  S le 2(1-I),I in[frac{1}{2},1] \ 0 & text{for}  S gt 2(1-I),Iin[frac{1}{2},1] end{cases}</script>
   
  
 </span><span class="katex-html"><span class="base"><span class="strut" style="height: 1em; vertical-align: -0.25em;"></span><span class="mord"><span class="mord mathdefault" style="margin-right: 0.10764em;">f</span><span class="msupsub"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.32833099999999993em;"><span class="" style="top: -2.5500000000000003em; margin-left: -0.10764em; margin-right: 0.05em;"><span class="pstrut" style="height: 2.7em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mathdefault mtight" style="margin-right: 0.07847em;">I</span><span class="mord mathdefault mtight" style="margin-right: 0.05764em;">S</span></span></span></span></span><span class="vlist-s">​</span></span><span class="vlist-r"><span class="vlist" style="height: 0.15em;"><span class=""></span></span></span></span></span></span><span class="mopen">(</span><span class="mord mathdefault" style="margin-right: 0.07847em;">I</span><span class="mpunct">,</span><span class="mspace" style="margin-right: 0.16666666666666666em;"></span><span class="mord mathdefault" style="margin-right: 0.05764em;">S</span><span class="mclose">)</span><span class="mspace" style="margin-right: 0.2777777777777778em;"></span><span class="mrel">=</span><span class="mspace" style="margin-right: 0.2777777777777778em;"></span></span><span class="base"><span class="strut" style="height: 5.76em; vertical-align: -2.63em;"></span><span class="minner"><span class="mopen"><span class="delimsizing mult"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 2.9500200000000003em;"><span class="" style="top: -1.59999em;"><span class="pstrut" style="height: 3.15em;"></span><span class="delimsizinginner delim-size4"><span class="">⎩</span></span></span><span class="" style="top: -1.59999em;"><span class="pstrut" style="height: 3.15em;"></span><span class="delimsizinginner delim-size4"><span class="">⎪</span></span></span><span class="" style="top: -1.89999em;"><span class="pstrut" style="height: 3.15em;"></span><span class="delimsizinginner delim-size4"><span class="">⎪</span></span></span><span class="" style="top: -2.19999em;"><span class="pstrut" style="height: 3.15em;"></span><span class="delimsizinginner delim-size4"><span class="">⎪</span></span></span><span class="" style="top: -3.1500100000000004em;"><span class="pstrut" style="height: 3.15em;"></span><span class="delimsizinginner delim-size4"><span class="">⎨</span></span></span><span class="" style="top: -4.30001em;"><span class="pstrut" style="height: 3.15em;"></span><span class="delimsizinginner delim-size4"><span class="">⎪</span></span></span><span class="" style="top: -4.60001em;"><span class="pstrut" style="height: 3.15em;"></span><span class="delimsizinginner delim-size4"><span class="">⎪</span></span></span><span class="" style="top: -4.90001em;"><span class="pstrut" style="height: 3.15em;"></span><span class="delimsizinginner delim-size4"><span class="">⎪</span></span></span><span class="" style="top: -5.20002em;"><span class="pstrut" style="height: 3.15em;"></span><span class="delimsizinginner delim-size4"><span class="">⎧</span></span></span></span><span class="vlist-s">​</span></span><span class="vlist-r"><span class="vlist" style="height: 2.45002em;"><span class=""></span></span></span></span></span></span><span class="mord"><span class="mtable"><span class="col-align-l"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 3.1300000000000003em;"><span class="" style="top: -5.130000000000001em;"><span class="pstrut" style="height: 3.008em;"></span><span class="mord"><span class="mord">6</span><span class="mord mathdefault" style="margin-right: 0.05764em;">S</span><span class="mord cjk_fallback" style="color: transparent;">哈</span><span class="mord cjk_fallback" style="color: transparent;">哈</span></span></span><span class="" style="top: -3.6900000000000004em;"><span class="pstrut" style="height: 3.008em;"></span><span class="mord"><span class="mord">0</span></span></span><span class="" style="top: -2.2500000000000004em;"><span class="pstrut" style="height: 3.008em;"></span><span class="mord"><span class="mord">6</span><span class="mord mathdefault" style="margin-right: 0.05764em;">S</span></span></span><span class="" style="top: -0.8100000000000002em;"><span class="pstrut" style="height: 3.008em;"></span><span class="mord"><span class="mord">0</span></span></span></span><span class="vlist-s">​</span></span><span class="vlist-r"><span class="vlist" style="height: 2.63em;"><span class=""></span></span></span></span></span><span class="arraycolsep" style="width: 1em;"></span><span class="col-align-l"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 3.1300000000000003em;"><span class="" style="top: -5.130000000000001em;"><span class="pstrut" style="height: 3.008em;"></span><span class="mord"><span class="mord text"><span class="mord">for</span></span><span class="mspace">&nbsp;</span><span class="mord mathdefault" style="margin-right: 0.05764em;">S</span><span class="mspace" style="margin-right: 0.2777777777777778em;"></span><span class="mrel">≤</span><span class="mspace" style="margin-right: 0.2777777777777778em;"></span><span class="mord">2</span><span class="mord mathdefault" style="margin-right: 0.07847em;">I</span><span class="mpunct">,</span><span class="mspace" style="margin-right: 0.16666666666666666em;"></span><span class="mord mathdefault" style="margin-right: 0.07847em;">I</span><span class="mspace" style="margin-right: 0.2777777777777778em;"></span><span class="mrel">∈</span><span class="mspace" style="margin-right: 0.2777777777777778em;"></span><span class="mopen">[</span><span class="mord">0</span><span class="mpunct">,</span><span class="mspace" style="margin-right: 0.16666666666666666em;"></span><span class="mord"><span class="mopen nulldelimiter"></span><span class="mfrac"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.845108em;"><span class="" style="top: -2.6550000000000002em;"><span class="pstrut" style="height: 3em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mtight">2</span></span></span></span><span class="" style="top: -3.23em;"><span class="pstrut" style="height: 3em;"></span><span class="frac-line" style="border-bottom-width: 0.04em;"></span></span><span class="" style="top: -3.394em;"><span class="pstrut" style="height: 3em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mtight">1</span></span></span></span></span><span class="vlist-s">​</span></span><span class="vlist-r"><span class="vlist" style="height: 0.345em;"><span class=""></span></span></span></span></span><span class="mclose nulldelimiter"></span></span><span class="mclose">]</span></span></span><span class="" style="top: -3.6900000000000004em;"><span class="pstrut" style="height: 3.008em;"></span><span class="mord"><span class="mord text"><span class="mord">for</span></span><span class="mspace">&nbsp;</span><span class="mord mathdefault" style="margin-right: 0.05764em;">S</span><span class="mspace" style="margin-right: 0.2777777777777778em;"></span><span class="mrel">&gt;</span><span class="mspace" style="margin-right: 0.2777777777777778em;"></span><span class="mord">2</span><span class="mord mathdefault" style="margin-right: 0.07847em;">I</span><span class="mpunct">,</span><span class="mspace" style="margin-right: 0.2777777777777778em;"></span><span class="mrel">∈</span><span class="mspace" style="margin-right: 0.2777777777777778em;"></span><span class="mopen">[</span><span class="mord">0</span><span class="mpunct">,</span><span class="mspace" style="margin-right: 0.16666666666666666em;"></span><span class="mord"><span class="mopen nulldelimiter"></span><span class="mfrac"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.845108em;"><span class="" style="top: -2.6550000000000002em;"><span class="pstrut" style="height: 3em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mtight">2</span></span></span></span><span class="" style="top: -3.23em;"><span class="pstrut" style="height: 3em;"></span><span class="frac-line" style="border-bottom-width: 0.04em;"></span></span><span class="" style="top: -3.394em;"><span class="pstrut" style="height: 3em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mtight">1</span></span></span></span></span><span class="vlist-s">​</span></span><span class="vlist-r"><span class="vlist" style="height: 0.345em;"><span class=""></span></span></span></span></span><span class="mclose nulldelimiter"></span></span><span class="mclose">]</span></span></span><span class="" style="top: -2.2500000000000004em;"><span class="pstrut" style="height: 3.008em;"></span><span class="mord"><span class="mord text"><span class="mord">for</span></span><span class="mspace">&nbsp;</span><span class="mord mathdefault" style="margin-right: 0.05764em;">S</span><span class="mspace" style="margin-right: 0.2777777777777778em;"></span><span class="mrel">≤</span><span class="mspace" style="margin-right: 0.2777777777777778em;"></span><span class="mord">2</span><span class="mopen">(</span><span class="mord">1</span><span class="mspace" style="margin-right: 0.2222222222222222em;"></span><span class="mbin">−</span><span class="mspace" style="margin-right: 0.2222222222222222em;"></span><span class="mord mathdefault" style="margin-right: 0.07847em;">I</span><span class="mclose">)</span><span class="mpunct">,</span><span class="mspace" style="margin-right: 0.16666666666666666em;"></span><span class="mord mathdefault" style="margin-right: 0.07847em;">I</span><span class="mspace" style="margin-right: 0.2777777777777778em;"></span><span class="mrel">∈</span><span class="mspace" style="margin-right: 0.2777777777777778em;"></span><span class="mopen">[</span><span class="mord"><span class="mopen nulldelimiter"></span><span class="mfrac"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.845108em;"><span class="" style="top: -2.6550000000000002em;"><span class="pstrut" style="height: 3em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mtight">2</span></span></span></span><span class="" style="top: -3.23em;"><span class="pstrut" style="height: 3em;"></span><span class="frac-line" style="border-bottom-width: 0.04em;"></span></span><span class="" style="top: -3.394em;"><span class="pstrut" style="height: 3em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mtight">1</span></span></span></span></span><span class="vlist-s">​</span></span><span class="vlist-r"><span class="vlist" style="height: 0.345em;"><span class=""></span></span></span></span></span><span class="mclose nulldelimiter"></span></span><span class="mpunct">,</span><span class="mspace" style="margin-right: 0.16666666666666666em;"></span><span class="mord">1</span><span class="mclose">]</span></span></span><span class="" style="top: -0.8100000000000002em;"><span class="pstrut" style="height: 3.008em;"></span><span class="mord"><span class="mord text"><span class="mord">for</span></span><span class="mspace">&nbsp;</span><span class="mord mathdefault" style="margin-right: 0.05764em;">S</span><span class="mspace" style="margin-right: 0.2777777777777778em;"></span><span class="mrel">&gt;</span><span class="mspace" style="margin-right: 0.2777777777777778em;"></span><span class="mord">2</span><span class="mopen">(</span><span class="mord">1</span><span class="mspace" style="margin-right: 0.2222222222222222em;"></span><span class="mbin">−</span><span class="mspace" style="margin-right: 0.2222222222222222em;"></span><span class="mord mathdefault" style="margin-right: 0.07847em;">I</span><span class="mclose">)</span><span class="mpunct">,</span><span class="mspace" style="margin-right: 0.16666666666666666em;"></span><span class="mord mathdefault" style="margin-right: 0.07847em;">I</span><span class="mspace" style="margin-right: 0.2777777777777778em;"></span><span class="mrel">∈</span><span class="mspace" style="margin-right: 0.2777777777777778em;"></span><span class="mopen">[</span><span class="mord"><span class="mopen nulldelimiter"></span><span class="mfrac"><span class="vlist-t vlist-t2"><span class="vlist-r"><span class="vlist" style="height: 0.845108em;"><span class="" style="top: -2.6550000000000002em;"><span class="pstrut" style="height: 3em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mtight">2</span></span></span></span><span class="" style="top: -3.23em;"><span class="pstrut" style="height: 3em;"></span><span class="frac-line" style="border-bottom-width: 0.04em;"></span></span><span class="" style="top: -3.394em;"><span class="pstrut" style="height: 3em;"></span><span class="sizing reset-size6 size3 mtight"><span class="mord mtight"><span class="mord mtight">1</span></span></span></span></span><span class="vlist-s">​</span></span><span class="vlist-r"><span class="vlist" style="height: 0.345em;"><span class=""></span></span></span></span></span><span class="mclose nulldelimiter"></span></span><span class="mpunct">,</span><span class="mspace" style="margin-right: 0.16666666666666666em;"></span><span class="mord">1</span><span class="mclose">]</span></span></span></span><span class="vlist-s">​</span></span><span class="vlist-r"><span class="vlist" style="height: 2.63em;"><span class=""></span></span></span></span></span></span></span><span class="mclose nulldelimiter"></span></span></span></span></span></span></span><font color="blue">这里是对 <span class="katex--inline"><span class="katex"><span class="katex-mathml">
 
  
   
    
     I
    
    
     ,
    
    
     S
    
   
   
    I,S
   
  
 </span><span class="katex-html"><span class="base"><span class="strut" style="height: 0.8777699999999999em; vertical-align: -0.19444em;"></span><span class="mord mathdefault" style="margin-right: 0.07847em;">I</span><span class="mpunct">,</span><span class="mspace" style="margin-right: 0.16666666666666666em;"></span><span class="mord mathdefault" style="margin-right: 0.05764em;">S</span></span></span></span></span> 进行联合处理的公式，也是根据范围来赋值处理就可。</font></p>

  我觉得这个系数应该用4才对，这样能保证你的I在0-1之间，当然我也用过了12这个系数(想想是这样的)，结果看下面：
在这里插入图片描述
  第5副图是用4做的系数，第6副图用的是12做的系数，同时第六幅图还对S分量也做了处理，感觉就是有点问题，但是不知道哪里有问题，毕竟马克思教我们要具体问题具体分析吗 ^ - ^

  就是可怜我的北登被整成这样了，第三第四幅图是我用MATLAB的histeq和adathisteq对I分量做了直方图均衡化的结果。
  做完后再把原图从HSI空间转回到RGB空间显示，但是效果不好，可能是图的问题吧，也可能像pitas在原文说的这种方法会出现原来图像不存在的I分量，即过饱和的I，导致转回RGB空间的时候出现异常。

3. 代码 

%coding = UTF8
%测试直方图均衡化的方法
%2020-10-23
%version1.0
%by neverland!

%读取图像
im = imread(‘hh.jpg’);
%在rgb通道作直方图均衡化
r = im(:,:,1);
g = im(:,:,2);
b = im(:,:,3);
r_ = histeq(r);
g_ = histeq(g);
b_ = histeq(b);
im_ = cat(3,r_,g_,b_);
%在hsi通道作直方图均衡化
im1 = rgb2hsv(im);
H = im1(:,:,1);
S = im1(:,:,2);
I = im1(:,:,3);
%复制变量
I_ = I;
I_2 = I;
S_ = S;
%对S变量进行处理
index3 = (S<1 & S>0);
S_(index3) = 6S(index3) - S(index3).^2;
%利用MATLAB自带的直方图均衡化
I_ = adapthisteq(I);
I_1 = histeq(I);
%利用pitas的理论
index1 = I<0.5;
index2 = I>0.5;
I_2(index1) = 12I(index1).^2;
I_2(index2) = 12*(1-I(index2)).^2;
%第一幅图histeq
im1_ = cat(3,H,S,I_);
im1_ = hsv2rgb(im1_);
%第二幅图用的是adathisteq
im2 = cat(3,H,S,I_1);
im2_ = hsv2rgb(im2);
%第三幅图用1996年的理论
im3 = cat(3,H,S,I_2);
im3_ = hsv2rgb(im3);
%再处理一次；
im4 = cat(3,H,S_,I_2);
im4_ = hsv2rgb(im4);
%分开显示下
subplot(2,3,1);imshow(im);title(‘原始图像’,‘FontSize’,20);
subplot(2,3,2);imshow(im_);title(‘RGB空间内作直方图均衡化’,‘fontsize’,20);
subplot(2,3,3);imshow(im1_);title(‘HSI空间内作直方图均衡化’,‘fontsize’,20);
subplot(2,3,4);imshow(im2_);title(‘HSI空间内作直方图均衡化’,‘fontsize’,20);
subplot(2,3,5);imshow(im3_);title(‘HSI空间内作直方图均衡化’,‘fontsize’,20);
subplot(2,3,6);imshow(im4_);title(‘HSI空间内作直方图均衡化’,‘fontsize’,20);

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34
  • 35
  • 36
  • 37
  • 38
  • 39
  • 40
  • 41
  • 42
  • 43
  • 44
  • 45
  • 46
  • 47
  • 48
  • 49
  • 50
  • 51
  • 52
  • 53
  • 54
  • 55

  其实adathisteq是对对比度受限的图做直方图均衡化的方法，
  而histeq是不加限制的做均衡化，当然是你人为选择方法的，而且我也不知道直接对I分量做直方图均衡化合不合理，网上blog好少，文献没读清楚，后续再改进吧。

4. 参考文献

[1].任洁. 彩色图像增强算法的研究与实现[D]. 武汉理工大学, 2013.
[2].Pitas I , Kiniklis P . Multichannel techniques in color image enhancement and modeling[J]. IEEE Transactions on Image Processing, 1996, 5(1):168-171.
[3].阮秋琦. 数字图像处理学[M]. 电子工业出版社, 2007.

最后，我将在另外一个账号写博客，有兴趣的可以关注。

最后

以上就是坚定小虾米为你收集整理的数字图像处理笔记(八)彩色图像和彩色图像直方图均衡化 1. 彩色空间 2. HSI空间进行直方图均衡化 3. 代码 4. 参考文献 的全部内容，希望文章能够帮你解决数字图像处理笔记(八)彩色图像和彩色图像直方图均衡化 1. 彩色空间 2. HSI空间进行直方图均衡化 3. 代码 4. 参考文献 所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。

本图文内容来源于网友提供，作为学习参考使用，或来自网络收集整理，版权属于原作者所有。
点赞(53)

相关文章

直方图均衡化(色调均化)（一）
直方图均衡化(色调均化)（一）
matlab实现彩色图像的直方图均衡化
matlab实现彩色图像的直方图均衡化
【论文笔记】投影仪-相机系统标定方法Simple, Accurate, and Robust Projector-Camera Calibration
【论文笔记】投影仪-相机系统标定方法Simple, Accurate, and Robust Projector-Camera Calibration
[图像增强]二. 直方图均衡化一. 直方图均衡化算法分为三个步骤二. 直方图均衡化某实现三. 举例四. 用途和说明
[图像增强]二. 直方图均衡化一. 直方图均衡化算法分为三个步骤二. 直方图均衡化某实现三. 举例四. 用途和说明
数字图像处理笔记(八)彩色图像和彩色图像直方图均衡化 1. 彩色空间 2. HSI空间进行直方图均衡化 3. 代码 4. 参考文献
数字图像处理笔记(八)彩色图像和彩色图像直方图均衡化 1. 彩色空间 2. HSI空间进行直方图均衡化 3. 代码 4. 参考文献
三种技术类型的3D摄像头大体总结 3D人脸识别
三种技术类型的3D摄像头大体总结 3D人脸识别
（10）查看RGB摄像头和深度摄像头RGB摄像头深度摄像头
（10）查看RGB摄像头和深度摄像头RGB摄像头深度摄像头
百度人脸SDK安卓平板USB红外(IR)/RGB摄像头图像混淆问题百度人脸SDK安卓平板USB红外(IR)/RGB摄像头图像混淆问题
百度人脸SDK安卓平板USB红外(IR)/RGB摄像头图像混淆问题百度人脸SDK安卓平板USB红外(IR)/RGB摄像头图像混淆问题

评论列表共有 0 条评论

立即
投稿
返回
顶部