前奏
先解释一下相移法中相机所捕获的条纹图案的数学表达式的含义

这里需要解释的是,表示第n张相移图上(x,y)点处的灰度值,
为条纹图背景值,
为调制强度函数。与上图中的变量解释不一样,查看了将近十几个人的文章,对a,b的含义,每个人的解释都不一样,那到底是什么含义呢?
可以看作是周围环境光的影响,可以看作是加性干扰项,
可以看作是相机本身对图像获取的强度偏差以及物体表面的反射特性所引起的乘性干扰项。
优秀的是,因为在求解相位值的过程中,只需要相移图的灰度值就可以,其他都会消掉。
言归正传,下面主要解释相移法中对相机和投影仪所要标定的系统信息是怎么去和相移法所求得的相位差进行联系进而求得所需要的高度值(三维信息)的。
一、最经典的光栅投影系统
采用相位测量剖面法,通过对物体的横截面进行分析,物体的深度信息以高度的形式进行求解,这种方法按照明光源分两种类型,一种是远心光路,所投射的光线为平行光,主要对小物体进行测量,尤其是高频光栅可以达到很高的测量精度,另一种是发散光路。
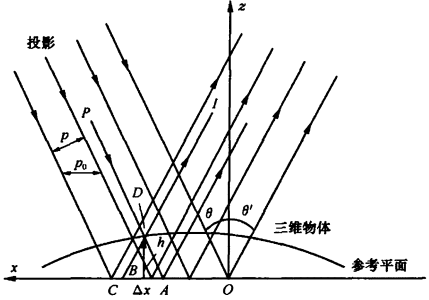
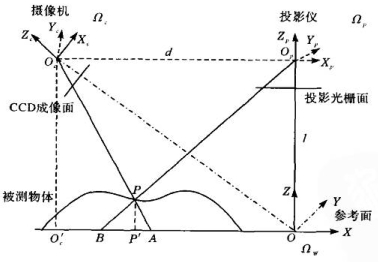
这里主要以发散照明结构为主,因为光的发散照明,所以光栅投射到参考平面的相位分布已经不是线性关系,所以需要一种相位映射算法来计算相位和高度h的关系。
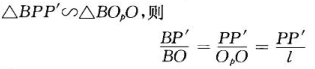
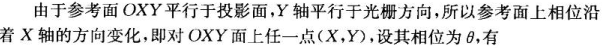
![]()
这里的是光栅节距,是光栅投射到参考平面后,在参考面上沿着X轴方向,相位变化一个周期(2
)对应的像素变化值。
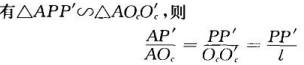
![]()
![]()
最后可得高度和相位的关系式:
![]()
和
是参考平面和物面上所对应的相位值。其中
是标定所获得,那怎么通过标定获得这些参数并将标定后的参数与这些值联系起来呢?
这里只要标定获得即可,标定的方法分为隐式标定和显示标定。
(1)隐式标定一
对上式进行变形可得:
假设在测量过程中,d要远远大于BA,则有,即有
即高度值是正比于PA之间的相位差,设比例系数为C,参考平面的高度为h0,可得
一般设置h0为0,我们只需要通过标定获得常数C即可,一个简单的标定方法如下:
测量一个高度已知(10mm)的立方体物体,上平面与下平面垂直,利用相移法测量该物体以获得解包裹后的相位图,假设相位图如下:
由于上下平面的高度一样,所以相位值一样,通过对截面图的上下两条线进行拟合,获得两条线之间的距离,也就获得了相位差,这里为20
1,上平面的点用一条线拟合为![]()
2,下平面的点用一条线拟合为![]()
3,计算两条线的距离为d。
所以可得 C=10/20 = 0.5(mm/rad)。
这样通过简单的标定就可以获得高度与相位差的关系。
说明:这里做了近似和拟合处理,而且没有用到投影仪的标定,求取的值是不精确的。
(2)隐式标定二
任然对于上式,这里的h0不再视作0,需要一起求解,操作过程如下:
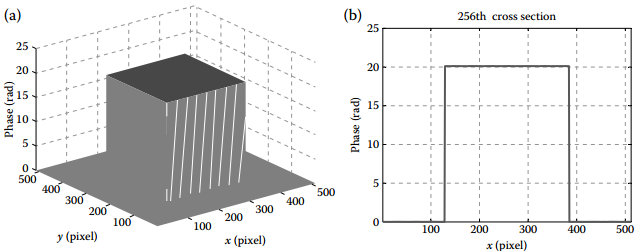
如下图所示,多次移动标定平面,得到多组标定平面的移动距离即高度h和相位差,再利用最小二乘法解出常数h0,C。
如上图所示,有10组标定平面H0,H1,H2...,H9,其中H1-H9的标定平面是H0分别平移h1,h2,h3...h9的距离获得的,平面上所有像素点的高度都是平移的距离。然后对于10个标定平面,分别投射相移光栅,利用相位测量轮廓法,求出每个标定平面上每个像素点的相位值,然后再减去H0上的相位值得到包裹相位差,然后解包裹后得到各自的相位差,然后根据上式利用最小二乘法求出参数h0和C。
(3)显式标定
对于显式标定,需要提前精确地测量投影仪-摄像机系统结构的具体参数。
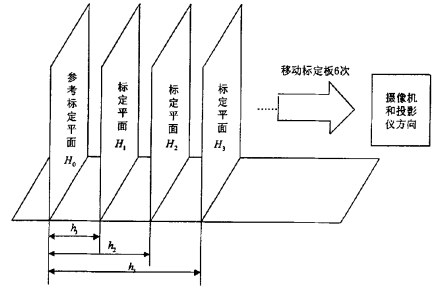
对于传统的相位测量轮廓法的系统由比较严格的条件限制,如下图
(1)CCD与DLP的光心必须水平;(2)CCD的光轴必须垂直于参考平面;
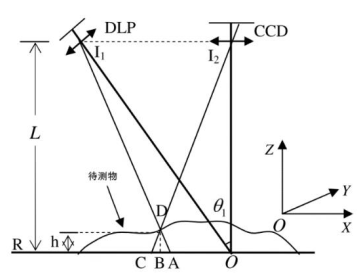
实际中上述条件难以满足,所以就有了下面改造后的系统,CCD与DLP的光心的连线与水平方向有一定的夹角,CCD的光轴与垂直方向有一定的夹角。
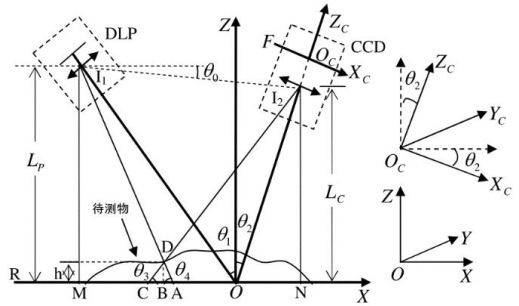
待测物体上的一点D的高度由三角形相似表示为:
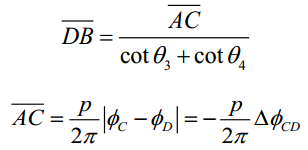
上式中p是投影仪投射到参考平面上的正弦条纹光栅的周期。为参考平面上C点的相位,
为物点D点的相位。
文献Contouring of artwork surface by fringe projection and FFT analysis中有:


然后根据相机模型和坐标转换关系可得相机坐标系下的相位-高度关系,具体不再推导。
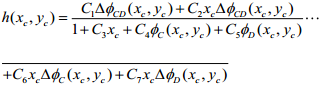
这只是几种处理方法,对传统的PMP方法的参数的显式标定我还在查,如果有了解的,可以联系我交流:857467352。
二、改进后的光栅投射剖面法
这种方法是达飞鹏老师对经典光栅投影系统做了改进,对相机和投影仪的位置关系的要求大大放宽,同时也不需要标定投影仪。
这种方法可以参考下面的文章,在这篇文章中有详细介绍,这里不再重复介绍。
《一种新的相位法三维轮廓测量系统模型及其标定方法研究》 达飞鹏
首先不标定投影仪,投影仪本身的畸变会影响标定精度,同时在标定方法上主要转为求解多变量方程的问题。
三、投影仪和相机都要标定的PMP
既然要用标定的信息,那就先对相机、投影仪和系统进行一次标定(张松的标定方法),这种方法也叫作三维散点标定法。
相机的标定(针对相机针孔模型):
所标定的信息有
内参:焦距,主点坐标,两个图像轴的倾斜度
外参:旋转矩阵和平移矩阵(世界坐标系到相机坐标系的变换)
相机的针孔模型如下图:
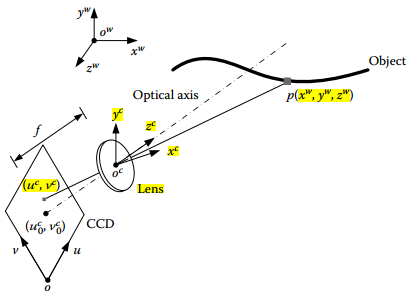

相机的内参和畸变标定还是用张正友的标定方法,伪代码如下:

操作步骤:
1、打印一张棋盘格,把它贴在一个平面上,作为标定物。
2、通过调整标定物或摄像机的方向,为标定物拍摄一些不同方向的照片。
3、从照片中提取棋盘格角点。
4、估算理想无畸变的情况下,五个内参和六个外参。
5、应用最小二乘法估算实际存在径向畸变下的畸变系数。
6、极大似然法,优化估计,提升估计精度。
投影仪也要标定内参和畸变参数,那问题来了,标定相机是对相机拍的图像进行标定,那投影仪只能投射怎么标定,投射的图像都是生成的,没得畸变呀。
如果可以使投影仪可以和相机一样,能够拍的图像的话,那我们就可以将投影仪当做相机来进行标定。大师张松在他的论文里给出的想法是将相机图像像素的强度转换为投影仪图像像素,使用相机捕获投影仪图像。关键是建立起相机图像和与投影仪图像像素之间的精确对应关系,他采用的方法是相移法。
由于相移法的相位方向是单方向的,如果相位方向是水平方向的,即同一个相位值是对应于一列的像素点,是没办法做到精确到像素的定位关系的。所以,张采用水平和垂直两个方向来进行相移操作,示意图如下。
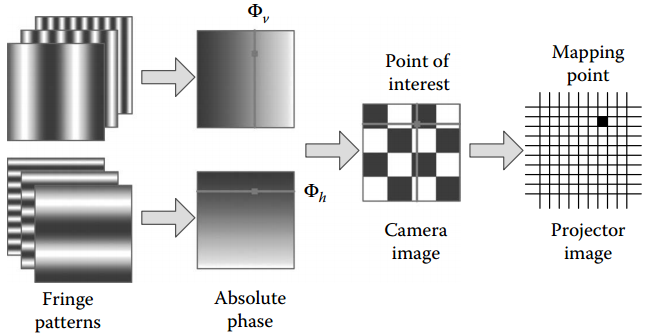
对于投影仪的标定方法,不解释为什么要这么做,只介绍怎么做。
使用的标定板如下图:

通过检测出这些圆点的圆心来进行标定,因为圆心周围没有颜色变化,所以相位是光滑的,如果使用格雷码,角点周围的颜色有变化,会导致相位的不连续。
操作步骤:
1,投影仪选择白光模式,相机捕获水平方向上的黑白条纹图案,并计算得到水平方向上的绝对相位值;
2,投影仪选择白光模式,相机捕获竖直方向上的黑白条纹图案,并计算得到竖直方向上的绝对相位值;
3,检测圆中心;
4,通过相位图建立的一对一映射,利用这些映射来确定那些相机圆心的投影仪圆心;
5,对于不同姿态下拍摄的图像,重复1-4的步骤;
6,利用标定相机的程序来标定投影仪的参数。
详细可以参考这篇论文:Novel calibration method for structured-light system with an out-of-focus projector
继续思考,相机和投影仪都单独标定完了,现在相机和投影仪的内参和畸变参数都已经获得了,即可以从二维的像素坐标系转化到三维的相机(投影仪)坐标系了,那系统标定的目的到底是什么?我们重建时的相位怎么用?外参好像还没有标定?好像这些问题都还没得解决!
由于相机和投影仪都是单独进行标定的,二维的像素坐标系转化到三维的相机(投影仪)坐标系是可以获得了,我们必须要建立从像素坐标系到世界坐标系下的关系。而世界坐标系是共同的,所以相机和投影仪都必须转换到世界坐标系,这就是外参的标定,关系如下。
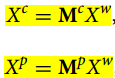
,
分别为相机坐标系和投影仪坐标系下某点的坐标矩阵,
为世界坐标系。
这样我们就发现了一个问题,那不是直接用相机的外参矩阵就可以直接建立相机的像素坐标系到世界坐标系的关系了,我们求的不就是某点世界坐标系下的三维坐标么,还用投影仪的标定干什么?可以思考两秒钟。。。
首先需要知道的是这是标定过程,我们会已知什么信息?
然后需要知道的是我们重建的方法是相移法去获得每个点的相位值,相位值怎么转换为世界坐标系下的三维坐标值?
最后在标定投影仪的时候我们用了水平和竖直方向的条纹图案来找相机和投影仪图案的一一对应关系,我们在重建时是否也需要拿到两个方向的相位图呢?
首先需要明确的是,我们为什么标定投影仪?
首先标定投影仪肯定是为了提高结构光重建的精度,但是主要是因为重建的方法模型的不同,标定投影仪的重建模型就不再是传统的相位测量轮廓法的相位——高度映射关系来求解深度信息,而是需要三角法来找相机和投影仪的对应点,将单目的求解转化为双目视觉的求解,用一个大佬的总结就是“投影仪的晶元尺寸太大,一个像素所表示的物理尺寸与相机的不一致”。
然后需要明确的是我们重建的关系,是相机的像素坐标()、投影仪的像素坐标
到世界坐标系下物体上任意一点的坐标(
)的关系,上面已经提到,这个关系的转换需要相机、投影仪的标定参数(包括内外参数),大致关系应该为:
(1)
在重建时,我们通过相移法获得了相机捕获图像的绝对相位图(相位图中每个图像坐标点都对应一个绝对相位值),并且已知投影仪投射图像对应的相位图,每个相机上的点会对应投影仪条纹图上相同绝对相位值的一条线,是多对一的问题,所以我们只需要投单方向的条纹图案。
接下来就是怎么获取投影仪条纹图对应相位的坐标了,这里是通过相位相同获得相机点和投影仪的一行(列)的坐标进行对应,有:
![]()
任取相机图像平面上一点(),相机在(
)点处的相位等于投影仪在
这一行的相位值,通过相位值去求得该相位值在投影仪图像平面上的
坐标值为:
,P为投影条纹图案一个周期内的像素个数。
回答了上面的几个问题,接下来就要用标定信息去推导上述最重要的公式(1)了:
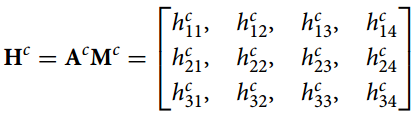
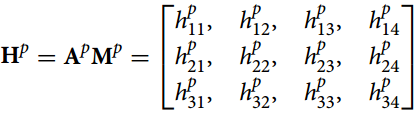
,
为相机的内参和外参,
,
为投影仪的内参和外参。
最后结果为:
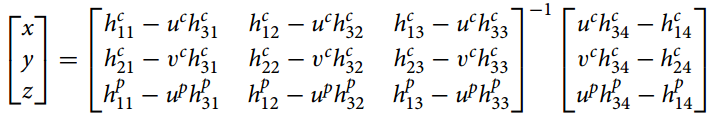
最后
以上就是直率金毛最近收集整理的关于结构光相移法中相机投影仪的标定信息如何与相位差联系的全部内容,更多相关结构光相移法中相机投影仪内容请搜索靠谱客的其他文章。








发表评论 取消回复