GMM聚类

高斯分布

GMM

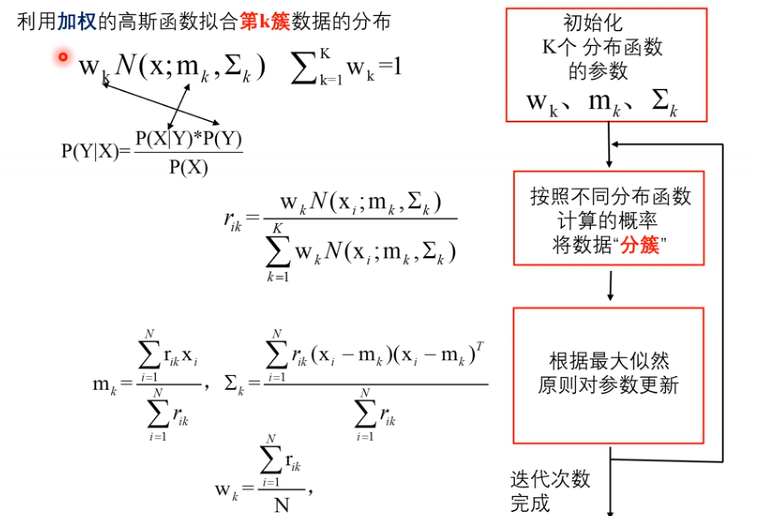
一、参数初始化

# GMM 参数初始化
# dataset: [N,D]
# K : cluster的个数（高斯成分的个数）
def init_GMM(dataset,K):
    N,D = np.shape(dataset)
    val_max = np.max(dataset,axis=0)
    val_min = np.min(dataset,axis=0)   
    centers = np.linspace(val_min,val_max,num=K+2) 
    mus = centers[1:-1,:]   
    sigmas = np.array([0.5*np.eye(D) for i in range(K)])  
    ws = 1.0/K * np.ones(K)
    
    return mus,sigmas,ws     # (K, D) (K, D, D) (K,)

二、计算 N(X;m,Σ)

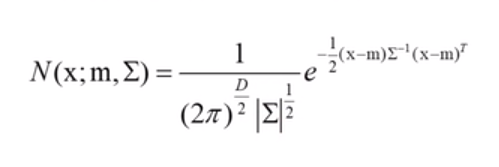
# 计算一个高斯pdf
# x(dataset): 数据[N,D]
# sigma 方差[D,D]
# mu 均值[1,D] ；注意这里的mu是数据的均值（不是mus）    
def getPdf(x,mu,sigma,eps=1e-12):
    N,D = np.shape(x)
    
    if D==1:
        sigma = sigma+eps
        A = 1.0 / (sigma)
        det = np.fabs(sigma[0])
    else:
        sigma = sigma + eps*np.eye(D)
        A = np.linalg.inv(sigma)    # np.linalg.inv()这里矩阵求逆
        det = np.fabs(np.linalg.det(sigma)) # np.linalg.det()矩阵求行列式
        
    # 计算系数
    factor = (2.0 * np.pi)**(D / 2.0) * (det)**(0.5)
    
    # 计算 pdf
    dx = x - mu
    pdf = [(np.exp(-0.5*np.dot(np.dot(dx[i],A),dx[i]))+eps)/ factor for i in range(N)]
    
    return pdf      

三、更新参数

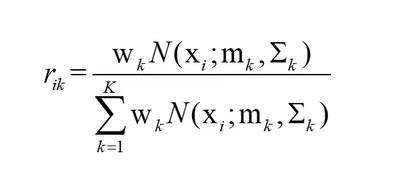
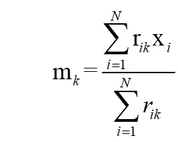
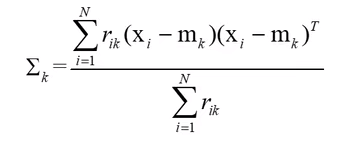
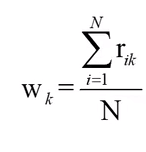
def train_GMM_step(dataset,mus,sigmas,ws):
    N,D = np.shape(dataset)
    K,D = np.shape(mus)
    # 计算样本在每个Cluster上的Pdf
    pdfs = np.zeros([N,K])
    for k in range(K):      # 这里算出N(x;m...)
        pdfs[:,k] = getPdf(dataset,mus[k],sigmas[k])
    
    # 获取r
    r = pdfs*np.tile(ws,(N,1))     
    r_sum = np.tile(np.sum(r,axis=1,keepdims=True),(1,K))  
    r = r/r_sum                    # 这里为R ik
    
    # 进行参数更新
    for k in range(K):
        r_k = r[:,k]               # r_k.shape=(N,)
        N_k = np.sum(r_k)
        r_k = r_k[:,np.newaxis]    # r_k.shape=(N,1)
        
        # 更新mu
        mu = np.sum(dataset*r_k,axis=0)/N_k   #[D,1]
        
        # 更新sigma
        dx = dataset - mu
        sigma = np.zeros([D,D])
        for i in range(N):
            sigma = sigma + r_k[i,0]*np.outer(dx[i],dx[i])  # np.outer用来求矩阵外积
        sigma = sigma/N_k
        
        # 更新w
        w = N_k/N
        mus[k] = mu
        sigmas[k] = sigma
        ws[k] = w
    
    return mus,sigmas,ws        # (K, D) (K, D, D) (K,)

四、GMM训练

# GMM训练
def train_GMM(dataset,K,m=10):
    mus,sigmas,ws = init_GMM(dataset,K)
    # print(mus,sigmas,ws)
    for i in range(m):
        # print("step: ",i)
        mus,sigmas,ws = train_GMM_step(dataset,mus,sigmas,ws)
        # print(mus,sigmas,ws)
    return mus,sigmas,ws

五、计算数据在每个模型上的似然值

def getlogPdfFromeGMM(dataset,mus,sigmas,ws):
    N,D = np.shape(dataset)
    K,D = np.shape(mus)
    
    weightedlogPdf = np.zeros([N,K])
    
    for k in range(K):    
        temp = getPdf(dataset,mus[k],sigmas[k],eps = 1e-12)  
        weightedlogPdf[:,k] = np.log(temp) + np.log(ws[k])  # 这里为公式log(w*N())
        
    return weightedlogPdf, np.sum(weightedlogPdf,axis=1)

六、利用GMM进行聚类（通过比较似然值）

def clusterByGMM(datas,mus,sigmas,ws):
    weightedlogPdf,_ = getlogPdfFromeGMM(datas,mus,sigmas,ws)
    labs = np.argmax(weightedlogPdf,axis=1)
    return labs  # 得到分类标签

测试：

# 作图
def draw_cluster(dataset,lab,dic_colors):
    plt.cla()
    vals_lab = set(lab.tolist())
    
    for i,val in enumerate(vals_lab):
        index = np.where(lab==val)[0]
        sub_dataset = dataset[index,:]
        plt.scatter(sub_dataset[:,0],sub_dataset[:,1],s=16.,color=dic_colors[i])

# GMM聚类测试
dic_colors = {0:(0.,0.5,0.),1:(0.8,0,0),2:(0.5,0.5,0),3:(0.5,0.5,0.9)}
a = np.random.multivariate_normal([2,2],[[.5,0],[0,.5]],200)
b = np.random.multivariate_normal([0,1],[[.5,0],[0,.5]],200)
c = np.random.multivariate_normal([1,4],[[.5,0],[0,.5]],200)
d = np.random.multivariate_normal([4,4],[[.5,0],[0,.5]],200)
dataset = np.r_[a,b,c,d]
# print(dataset.shape)

# 真实标签
lab_true = np.r_[np.zeros(200),np.ones(200),2*np.ones(200),3*np.ones(200)].astype(int)

# 绘制原始数据散点图
draw_cluster(dataset,lab_true,dic_colors)

原始数据

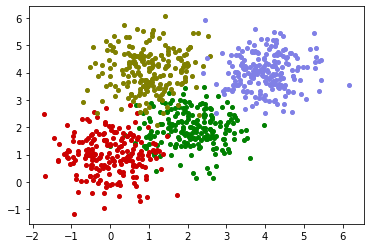
# 训练GMM
mus,sigmas,ws = train_GMM(dataset,K=4,m=10)
#print(mus,sigmas,ws)

# 进行聚类
labs_GMM = clusterByGMM(dataset,mus,sigmas,ws)
#print(labs_GMM)

# 绘制聚类后图片
draw_cluster(dataset,labs_GMM,dic_colors)

GMM聚类效果

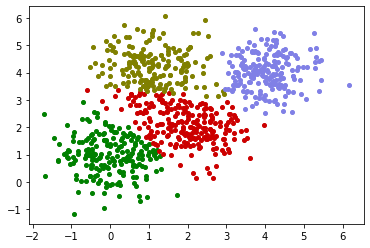
GMM与K-means比较

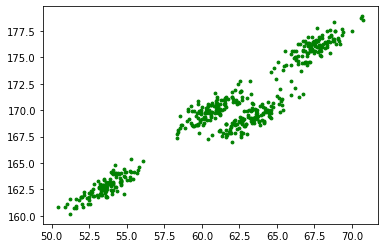
原始数据

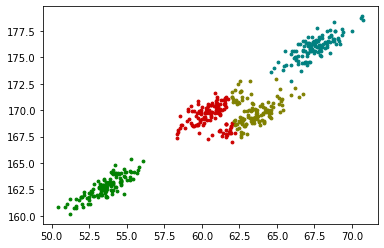
K-means聚类效果

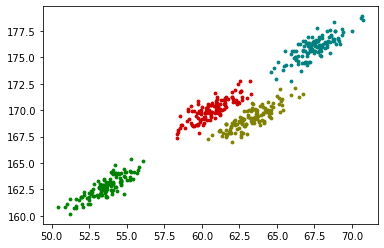
GMM聚类效果

最后

以上就是和谐微笑为你收集整理的GMM聚类GMM聚类的全部内容，希望文章能够帮你解决GMM聚类GMM聚类所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。