采用EM估计GMM的参数

      通常采用EM对GMM参数进行估计。EM（期望值最大，Expectation Maximum）算法思想比较简单，主要分为两个步骤，估计步骤E-step和最大化步骤M-step。首先利用样本对参数进行估计，然后在M-step中将需要估计的参数最大化（通常是求其最大似然估计），不断地迭代此两个步骤，直到收敛。

      下面写一下采用EM估计GMM的步骤：

      1、初始值确定。

       方案1：将协方差矩阵设为单位矩阵，每个模型的先验概率设为1/M，均值设为随机数，即：

      方案2：有k均值（k-mean）聚类算法对样本进行聚类，利用各类的均值作为均值初始值，并计算协方差矩阵作为初始值，每个模型的先验概率取各类样本占样本总数的比例。

      2、估计步骤（E-step）

      3、最大化步骤（M-step）

      分别按下式更新权值、均值和协方差矩阵：

      有的文献把协方差矩阵当作对角阵处理，则有

      但是这样的假设会给最终结果带来误差，故在运算速度能保证的情况下最好还是采用正常的协方差矩阵估计方法。

      4、收敛条件

      方案1：不断地迭代E和M步骤，直到：

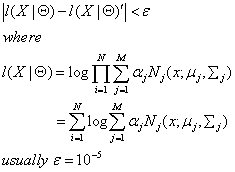
      方案2：不断地迭代E和M步骤，直到：

      方案1和方案2最终效果接近，但方案2明显运算量小，故一般使用方案2。

      整个估计过程就是这样，其中有很多公式推导，没有仔细研究，有时间再看看吧。

      （以上内容根据某资料整理，如有雷同，不胜荣幸）

最后

以上就是潇洒过客为你收集整理的采用EM估计GMM的参数的全部内容，希望文章能够帮你解决采用EM估计GMM的参数所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。