用PCA降维

PCA将数据投射到一个低维子空间实现降维。例如，二维数据集降维就是把点投射成一条线，数据集的每个样本都可以用一个值表示，不需要两个值。三维数据集可以降成二维，就是把变量映射成一个平面。一般情况下， 维数据集可以通过映射降成维子空间。

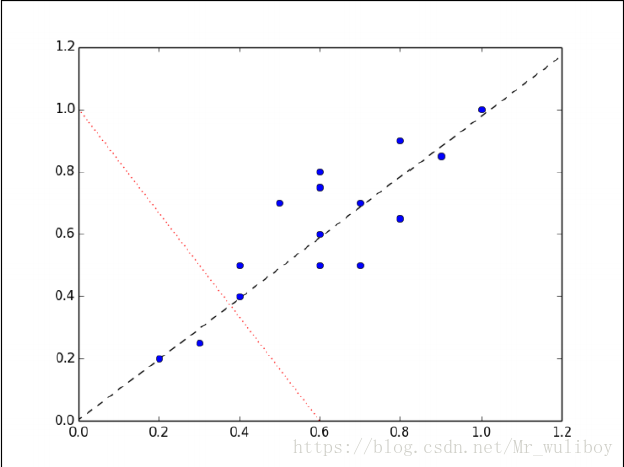
显然，样本映射到虚线的变化比映射到点线的变化小。实际上，这条虚线就是第一主成分。第二主成分必须与第一主成分正交，也就是说第二主成分必须是在统计学上独立的，会出现在与第一主成分垂直的方向，如下图所示：

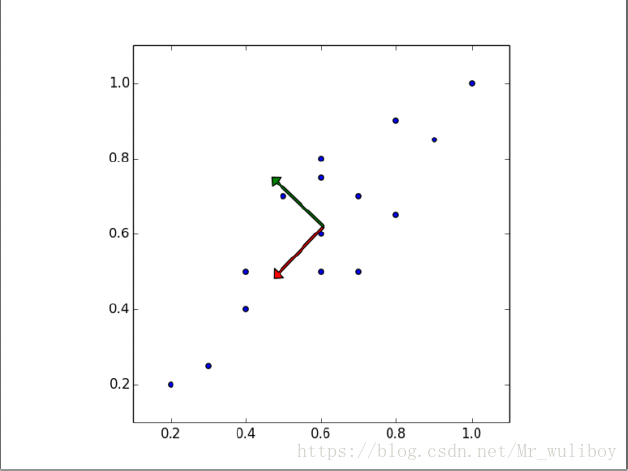
后面的每个主成分也会尽量多的保留剩下的变量，唯一的要求就是每一个主成分需要和前面的主成分正交。

方差，协方差和协方差矩阵

方差（Variance）是度量一组数据分散的程度。方差是各个样本与样本均值的差的平方和的均值：

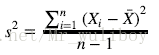
协方差（Covariance）是度量两个变量的变动的同步程度，也就是度量两个变量线性相关性程度。如果两个变量的协方差为0，则统计学上认为二者线性无关。注意两个无关的变量并非完全独立，只是没有线性相关性而已。计算公式如下：

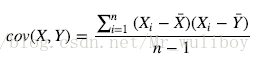
如果协方差不为0，如果大于0表示正相关，小于0表示负相关。当协方差大于0时，一个变量增大是另一个变量也会增大。当协方差小于0时，一个变量增大是另一个变量会减小。协方差矩阵（Covariance matrix）由数据集中两两变量的协方差组成。矩阵的第个元素是数据集中第和第（i,j）个元素的协方差。例如，三维数据的协方差矩阵如下所示：

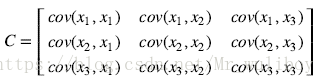
我们可以通过Numpy检验我们手算的特征向量。eig函数返回特征值和特征向量的元组：

import numpy as np
w, v = np.linalg.eig(np.array([[1, -2], [2, -3]]))
print('特征值：{}n特征向量：{}'.format(w,v))

输出结果如下：

特征值：[-0.99999998 -1.00000002]
特征向量：[[ 0.70710678 0.70710678]
[ 0.70710678 0.70710678]]

用PCA实现高维数据可视化

二维或三维数据更容易通过可视化发现模式。一个高维数据集是无法用图形表示的，但是我们可以通过降维方法把它降成二维或三维数据来可视化。

Fisher1936年收集了三种鸢尾花分别50个样本数据（Iris Data）：Setosa、Virginica、Versicolour。
解释变量是花瓣（petals）和萼片（sepals）长度和宽度的测量值，响应变量是花的种类。鸢尾花数
据集经常用于分类模型测试，scikit-learn中也有。让我们把iris数据集降成方便可视化的二维数
据：

%matplotlib inline
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
from sklearn.datasets import load_iris

#首先，我们导入鸢尾花数据集和PCA估计器。PCA类把主成分的数量作为超参数，和其他估计器一
#样，PCA也用fit_transform()返回降维的数据矩阵：

data = load_iris()
y = data.target
X = data.data
pca = PCA(n_components=2)#其中参数n_components表示保留的特征数，默认为1。如果设置成‘mle’,那么会自动确定保留的特#征数
reduced_X = pca.fit_transform(X)

red_x, red_y = [], []
blue_x, blue_y = [], []
green_x, green_y = [], []
for i in range(len(reduced_X)):
    if y[i] == 0:
        red_x.append(reduced_X[i][0])
        red_y.append(reduced_X[i][1])
    elif y[i] == 1:
        blue_x.append(reduced_X[i][0])
        blue_y.append(reduced_X[i][1])
    else:
        green_x.append(reduced_X[i][0])
        green_y.append(reduced_X[i][1])
plt.scatter(red_x, red_y, c='r', marker='x')
plt.scatter(blue_x, blue_y, c='b', marker='D')
plt.scatter(green_x, green_y, c='g', marker='.')#绘制scatter()散点图
plt.show()

运行结果如下图所示：

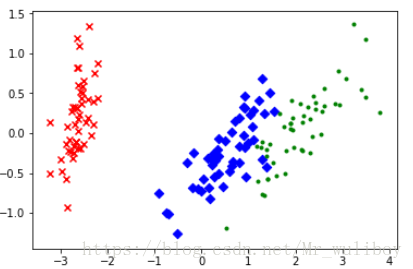
最后

以上就是寒冷故事为你收集整理的sk-learn 学习笔记七用PCA降维的全部内容，希望文章能够帮你解决sk-learn 学习笔记七用PCA降维所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。