概述
图像锐化处理
- 目的：突出图像的细节，或者增强被模糊了的细节，增强
图像边缘,便于提取目标物体的边界 - 图像边缘的特点：在边缘上的灰度变化比较平缓，而在边缘两侧灰度变化较快，梯度值较大。通常是局部不连续的，且亮度变化最显著的部分。
锐化的基本方法
微分运算
在数学上对于离散的数据，使用差分来定义一元函数
f
(
x
)
f(x)
f(x)的一阶微分,公式如下
∂
f
∂
x
=
f
(
x
+
1
)
−
f
(
x
)
frac{partial f}{partial x}=f(x+1)-f(x)
∂x∂f=f(x+1)−f(x)
再用差分定义一元函数
f
(
x
)
f(x)
f(x)的二阶微分，则公式如下
∂
2
f
∂
x
2
=
f
(
x
+
1
)
+
f
(
x
−
1
)
−
2
f
(
x
)
frac{partial^2 f}{partial x^2}=f(x+1)+f(x-1)-2f(x)
∂x2∂2f=f(x+1)+f(x−1)−2f(x)
上述公式是一元的。同理，我们也可以推导到二元，不过对于二元，就变成所谓的偏导数了
单向微分运算
公式如下(右列-左列)
G
(
i
,
j
)
=
f
(
i
,
j
)
−
f
(
i
−
1
,
j
)
G(i,j)=f(i,j)-f(i-1,j)
G(i,j)=f(i,j)−f(i−1,j)
或者，如下(下一行-上一行)
G
(
i
,
j
)
=
f
(
i
,
j
)
−
f
(
i
−
1
,
j
)
G(i,j)=f(i,j)-f(i-1,j)
G(i,j)=f(i,j)−f(i−1,j)
我们可以用代码模拟实现一下，当我们对图像进行上述两种微分，会产生什么效果?
#右列-左列
def margin_RCL(self):
img_buf=np.copy(self.Img)
for x in range(1,len(self.Img[0])):
img_buf[:,x,:]=np.abs(self.Img[:,x,:]-self.Img[:,x-1,:])
self.Img=img_buf
#下-上
def margin_DCU(self):
img_buf=np.copy(self.Img)
for y in range(0,len(self.Img)-1):
img_buf[y,:,:]=np.abs(self.Img[y+1,:,:]-self.Img[y,:,:])
self.Img=img_buf
原图如下
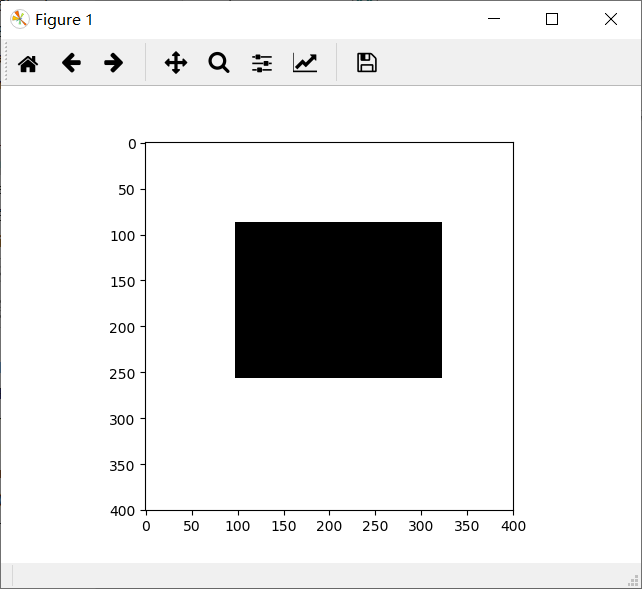
横向微分算法跑完之后，图像如下
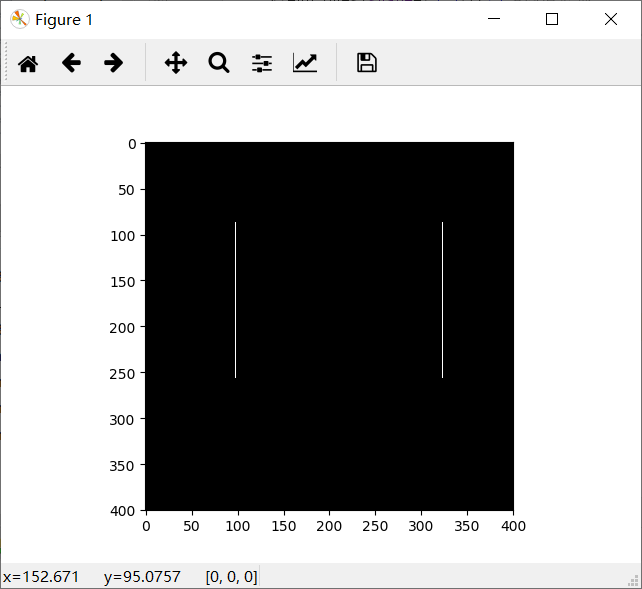
纵向微分计算之后
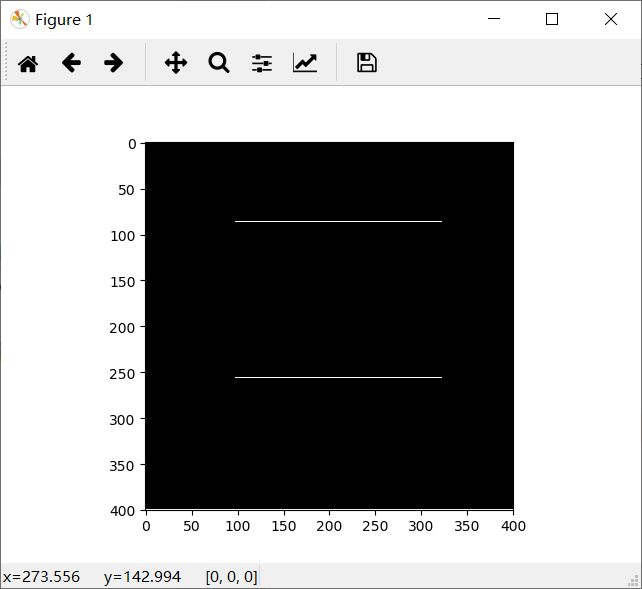
可以看到，我们成功的找到了边界
微分运算的作用：微分运算的结果反映了图像亮度变化率的大小；像素值保持不变的区域相减结果为0，即像素为黑；像素值变化剧烈的区域，相减结果得到较大的变化率，像素灰度值差别越大，则得到的像素就越亮
双向一次微分
其公式如下:
G
(
i
,
j
)
=
[
f
(
i
,
j
)
−
f
(
i
,
j
−
1
)
]
2
+
[
f
(
i
,
j
)
−
f
(
i
−
1
,
j
)
]
2
G(i,j)=sqrt {[f(i,j)-f(i,j-1)]^2+[f(i,j)-f(i-1,j)]^2}
G(i,j)=[f(i,j)−f(i,j−1)]2+[f(i,j)−f(i−1,j)]2
#双向一次微分
def margin_DoubleDere(self):
img_buf=np.copy(self.Img)
for y in range(1,len(self.Img)):
for x in range(1,len(self.Img[y])):
img_buf[y,x]=np.sqrt((self.Img[y,x,:]-self.Img[y,x-1,:])**2+(self.Img[y,x,:]-self.Img[y-1,x,:])**2)
self.Img=img_buf
效果图如下
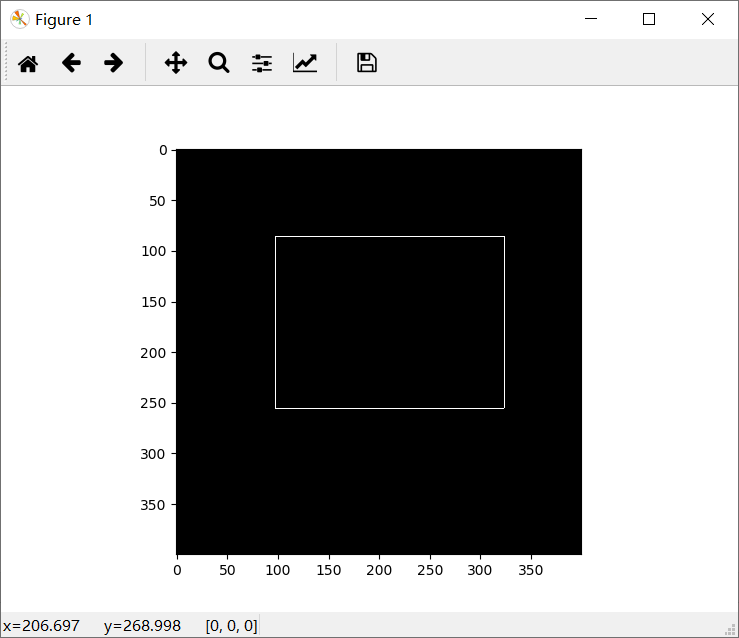
梯度运算
▽
f
=
[
∂
f
∂
x
∂
f
∂
y
]
bigtriangledown f=begin{bmatrix} frac{partial f}{partial x}\ frac{partial f}{partial y} end{bmatrix}
▽f=[∂x∂f∂y∂f]
因为上述为矢量，不好处理，所以我们将其转化为下述标量
▽
f
≈
∣
G
x
∣
+
∣
G
y
∣
bigtriangledown fapprox |G_x|+|G_y|
▽f≈∣Gx∣+∣Gy∣
或者
▽
f
≈
(
G
x
2
+
G
y
2
)
1
2
bigtriangledown fapprox (G_x^2+G_y^2)^{frac{1}{2}}
▽f≈(Gx2+Gy2)21
各种算子
- Robert提出的交叉微分算子，如下
[ Z 1 Z 2 Z 3 Z 4 Z 5 Z 6 Z 7 Z 8 Z 9 ] begin{bmatrix} Z_1 & Z_2 &Z_3 \ Z_4 &Z_5 & Z_6\ Z_7 &Z_8 & Z_9 end{bmatrix} ⎣⎡Z1Z4Z7Z2Z5Z8Z3Z6Z9⎦⎤
G x = Z 9 − Z 5 G y = Z 8 − Z 6 ▽ f ≈ ∣ G x ∣ + ∣ G y ∣ G_x=Z_9-Z_5\ G_y=Z_8-Z_6\ bigtriangledown f approx |G_x|+|G_y| Gx=Z9−Z5Gy=Z8−Z6▽f≈∣Gx∣+∣Gy∣
- Sobel算子
[ Z 1 Z 2 Z 3 Z 4 Z 5 Z 6 Z 7 Z 8 Z 9 ] begin{bmatrix} Z_1 & Z_2 &Z_3 \ Z_4 &Z_5 & Z_6\ Z_7 &Z_8 & Z_9 end{bmatrix} ⎣⎡Z1Z4Z7Z2Z5Z8Z3Z6Z9⎦⎤
[ − 1 − 2 − 1 0 0 0 1 2 1 ] begin{bmatrix} -1 & -2 &-1\ 0&0& 0\ 1&2& 1 end{bmatrix} ⎣⎡−101−202−101⎦⎤
[ − 1 0 1 − 2 0 2 − 1 0 1 ] begin{bmatrix} -1 & 0 &1\ -2&0& 2\ -1&0& 1 end{bmatrix} ⎣⎡−1−2−1000121⎦⎤
G
x
=
(
Z
7
+
2
Z
8
+
Z
9
)
−
(
Z
1
+
2
Z
2
+
Z
3
)
G
y
=
(
Z
3
+
2
Z
6
+
Z
9
)
−
(
Z
1
+
2
Z
4
+
Z
7
)
G_x=(Z_7+2Z_8+Z_9)-(Z_1+2Z_2+Z_3)\ G_y=(Z_3+2Z_6+Z_9)-(Z_1+2Z_4+Z_7)
Gx=(Z7+2Z8+Z9)−(Z1+2Z2+Z3)Gy=(Z3+2Z6+Z9)−(Z1+2Z4+Z7)
Sorbel算子既有平滑作用又有微分作用
- Prewitt算子
模板如下
[ − 1 − 1 − 1 0 0 0 1 1 1 ] begin{bmatrix} -1 & -1 &-1\ 0&0& 0\ 1&1& 1 end{bmatrix} ⎣⎡−101−101−101⎦⎤
[
−
1
0
1
−
1
0
1
−
1
0
1
]
begin{bmatrix} -1 & 0 &1\ -1&0& 1\ -1&0& 1 end{bmatrix}
⎣⎡−1−1−1000111⎦⎤
G
x
=
(
Z
7
+
Z
8
+
Z
9
)
−
(
Z
1
+
Z
2
+
Z
3
)
G
y
=
(
Z
3
+
Z
6
+
Z
9
)
−
(
Z
1
+
Z
4
+
Z
7
)
G_x=(Z_7+Z_8+Z_9)-(Z_1+Z_2+Z_3)\ G_y=(Z_3+Z_6+Z_9)-(Z_1+Z_4+Z_7)
Gx=(Z7+Z8+Z9)−(Z1+Z2+Z3)Gy=(Z3+Z6+Z9)−(Z1+Z4+Z7)
- 拉普拉斯算子(二次微分)
对于x方向,如下
∂ 2 f ∂ x 2 = f ( x + 1 ) + f ( x − 1 ) − 2 f ( x ) frac{partial^2 f}{partial x^2}=f(x+1)+f(x-1)-2f(x) ∂x2∂2f=f(x+1)+f(x−1)−2f(x)
对于y方向,如下
∂ 2 f ∂ y 2 = f ( y + 1 ) + f ( y − 1 ) − 2 f ( y ) frac{partial^2 f}{partial y^2}=f(y+1)+f(y-1)-2f(y) ∂y2∂2f=f(y+1)+f(y−1)−2f(y)
上述结果，相加，既得如下
▽
2
f
=
f
(
x
+
1
,
y
)
+
f
(
x
−
1
,
y
)
+
f
(
x
,
y
+
1
)
+
f
(
x
,
y
−
1
)
−
4
f
(
x
)
bigtriangledown^2 f=f(x+1,y)+f(x-1,y)+f(x,y+1)+f(x,y-1)-4f(x)
▽2f=f(x+1,y)+f(x−1,y)+f(x,y+1)+f(x,y−1)−4f(x)
所以，我们推导出，其模板如下
[
0
1
0
1
−
1
1
0
1
0
]
begin{bmatrix} 0 & 1 & 0\ 1 & -1 &1 \ 0 &1 &0 end{bmatrix}
⎣⎡0101−11010⎦⎤
所以，我们可以用上述模板，通过用卷积的方法，来求得图像的二次微分。该算子强化突变，弱化慢变
如果我们想保持物体背景，该怎么办呢？
我们可以将原始图像和对应的拉普拉斯图像叠加在一起，这样既可以保持锐化效果，又能复原背景信息
g
(
x
)
=
{
f
(
x
,
y
)
−
▽
2
f
(
x
,
y
)
中
心
系
数
为
负
f
(
x
,
y
)
+
▽
2
f
(
x
,
y
)
中
心
系
数
为
正
g(x)=left{begin{matrix} f(x,y)-triangledown^2f(x,y) &中心系数为负\ f(x,y)+triangledown^2f(x,y) &中心系数为正 end{matrix}right.
g(x)={f(x,y)−▽2f(x,y)f(x,y)+▽2f(x,y)中心系数为负中心系数为正
我们可以对其进行化简，得到如下公式
g
(
x
,
y
)
=
5
f
(
x
,
y
)
−
[
f
(
x
+
1
,
y
)
+
f
(
x
−
1
,
y
)
+
f
(
x
,
y
+
1
)
+
f
(
x
,
y
−
1
)
]
g(x,y)=5f(x,y)-[f(x+1,y)+f(x-1,y)+f(x,y+1)+f(x,y-1)]
g(x,y)=5f(x,y)−[f(x+1,y)+f(x−1,y)+f(x,y+1)+f(x,y−1)]
通过
g
(
x
,
y
)
g(x,y)
g(x,y)的表达式，我们可以求出其模板
[
0
−
1
0
−
1
5
−
1
0
−
1
0
]
begin{bmatrix} 0 &-1 &0 \ -1 & 5 &-1 \ 0&-1 & 0 end{bmatrix}
⎣⎡0−10−15−10−10⎦⎤
-
高斯-拉普拉斯算子
这种算子是效果更好的边缘检测器，把高斯平滑器和拉普拉斯锐化结合起来。总体效果就是，先平滑去噪声，然后再进行边缘检测，
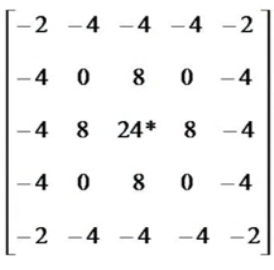
高频提升滤波器微分运算可以用来求信号的变化率，可以加强高频分量信号。但是微分处理后的图像非常暗，如果我们想要保持物体的背景，那么就得使用这种滤波器了
其公式如下
g ( x , y ) = a f ( x , y ) ± ▽ f ( x , y ) g(x,y)=af(x,y)pm bigtriangledown f(x,y) g(x,y)=af(x,y)±▽f(x,y)
自适应检测
因为一个物体的边界方向有很多，所以我们可以采用多个不同方向的算子来计算。然后找出各个算子所计算结果的最大值即为最终结果。
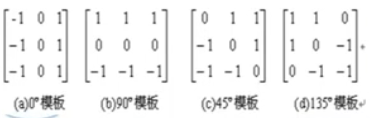
实现步骤基本如下：
- 将所有的边缘模板逐一作用于图像中的每一个像素,产生最大输出值的边缘模板方向,表示该点边缘的方向，
- 如果所有方向上的边缘模板接近于零，则该点处没有边缘;
- 如果所有方向上的边缘模板输出值都近似相等，没有可靠边缘方向。
最后
以上就是谨慎哑铃为你收集整理的图像锐化的基本方法图像锐化处理的全部内容，希望文章能够帮你解决图像锐化的基本方法图像锐化处理所遇到的程序开发问题。
如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。
发表评论 取消回复