1.主成分分析的基本思想

我们处理的问题多是多指标变量问题，由于多个变量之间往往存在着一定程度的相关性，人们希望能通过线性组合的方式从这些指标中尽可能快的提取信息。当第一个组合不能提取更多信息时，再考虑第二个线性组合。继续这个过程，直到提取的信息与原指标差不多时为止。

2. 主成分分析的作用

一般说来，在主成分分析适用的场合，用较少的主成分就可以得到较多的信息量。以各个主成分为分量，就得到一个更低维的随机向量；主成分分析的作用就是在降低数据“维数”的同时又保留了原数据的大部分信息。

3. 主成分分析中累积贡献率

4. 根据协差阵进行主成分分析和根据相关阵进行主成分分析的区别

相关阵求得的主成分与协差阵求得的主成分一般情况是不相同的。从协方差矩阵出发的，其结果受变量单位的影响。主成分倾向于多归纳方差大的变量的信息，对于方差小的变量就可能体现得不够，也存在“大数吃小数”的问题。实际表明，这种差异有时很大。我们认为，如果各指标之间的数量级相差悬殊，特别是各指标有不同的物理量纲的话，较为合理的做法是使用R代替∑。对于研究经济问题所涉及的变量单位大都不统一，采用R代替∑后，可以看作是用标准化的数据做分析，这样使得主成分有现实经济意义，不仅便于剖析实际问题，又可以避免突出数值大的变量。

5. 习题介绍

待完成

6. 主成分分析例子实现

问题提出
为了研究我国2005年第1、2季度31个省、市、自治区城镇居民家庭收支基本情况，收集以下5个变量：
X1：平均每户人口（人）；
X2：平均每户就业人口（人）；
X3：平均每一就业者负担人数（人）；
X4：平均每人实际可支配收入（元）；
X5：平均每人消费性支出（元）。
利用SPSS软件实现主成分分析。

实现步骤与分析：
将原始数据输入SPSS数据编辑窗口，将5个变量分别命名为x1_{x5。在SPSS窗口中选择分析→降维→因子分析菜单项，调出因子分析主对话框，并将变量x1}x5移入Variables框中，其他均保持系统默认选项，单击OK按钮，执行因子分析过程。

得到检验结果为：

由检验的结果可知,检验的P值接近于0，远小于0.05，说明可以做主成分分析

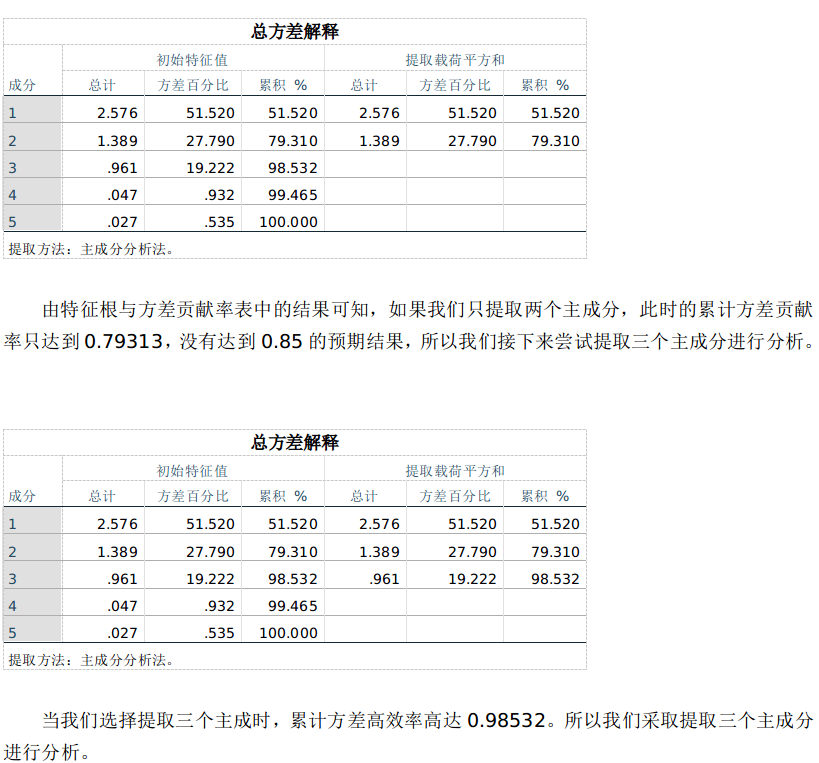
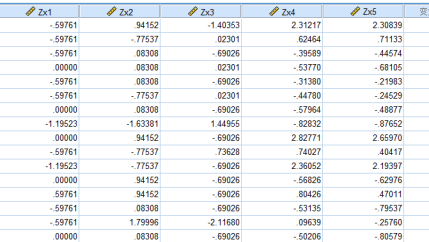
接下来我们将X1-X5进行标准化得到ZX1-ZX5如下所示：

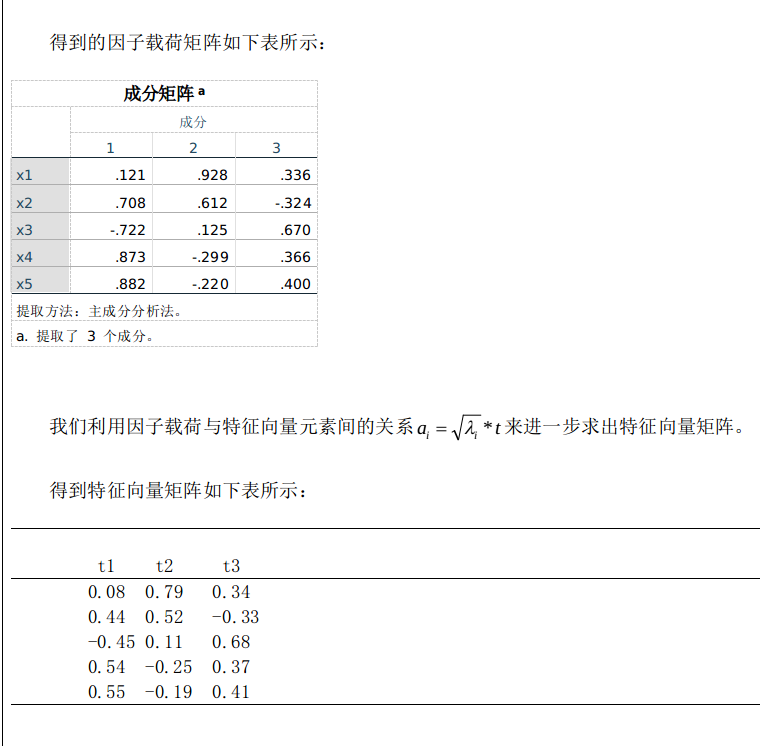
由特征向量矩阵的标准化后的变量表，我们可以得到三个主成分的表达式，表达式分别为：
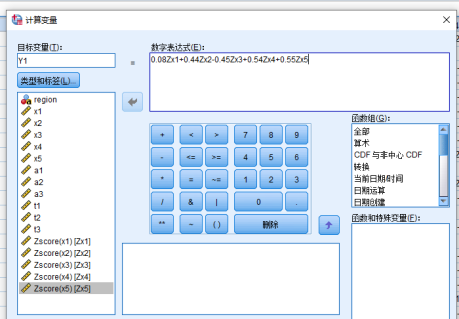
Y1=0.08X1*+0.44X2*-0.45X3*+0.54X4*+0.55X5*
Y2=0.79X1*+0.52X2*+0.11X3*-0.25X4*-0.19X5*
Y3=0.34X1*-0.33X2*+0.68X3*+0.37X4*+0.41X5*

在SPSS中根据ZXi(i=1,2,3,4,5)计算各个地区的Y1，Y2和Y3的值，得到结果如下：

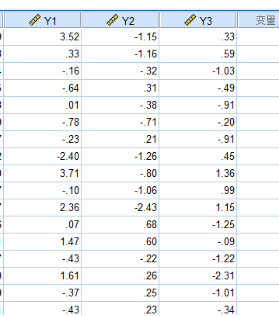
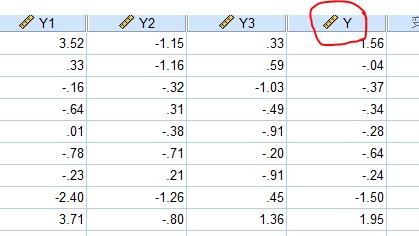
得到主成分得分后我们再根据主成分方差所占百分比乘以各主成分得分进而求出各省的综合得分，即Y=0.5152Y1+0.2779Y2+0.19222*Y3
得到结果如下：

现在我们对综合得分Y进行排序，排序结果为：

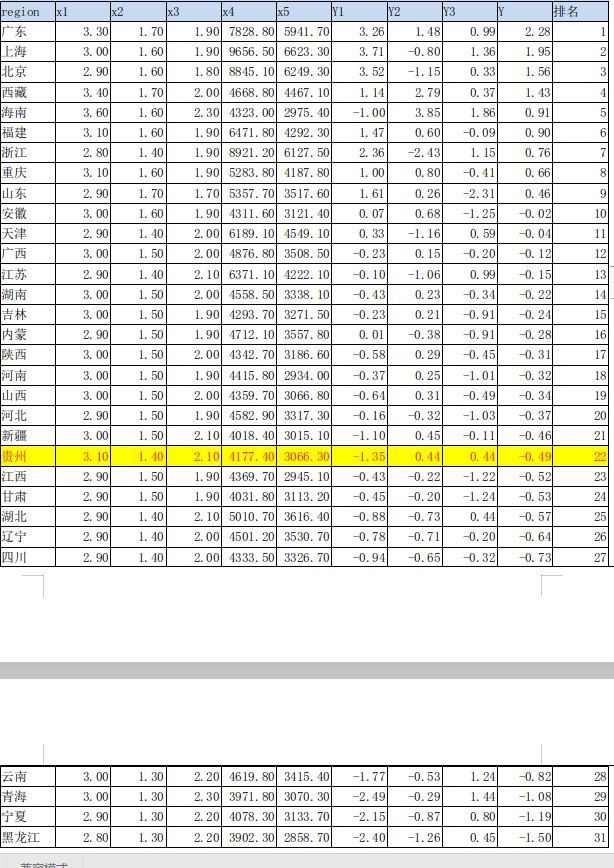
根据结果我们可以进行相应的推断分析

最后

以上就是现代啤酒为你收集整理的多元统计：主成分分析1.主成分分析的基本思想2. 主成分分析的作用3. 主成分分析中累积贡献率4. 根据协差阵进行主成分分析和根据相关阵进行主成分分析的区别5. 习题介绍6. 主成分分析例子实现的全部内容，希望文章能够帮你解决多元统计：主成分分析1.主成分分析的基本思想2. 主成分分析的作用3. 主成分分析中累积贡献率4. 根据协差阵进行主成分分析和根据相关阵进行主成分分析的区别5. 习题介绍6. 主成分分析例子实现所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。