本总结是是个人为防止遗忘而作，不得转载和商用。

 

       说明：此篇是作者对“ EM ”的第二次总结，因此可以算作对上次总结的查漏补缺以及更进一步的理解，所以很多在第一次总结中已经整理过的内容在本篇中将不再重复，如果你看的有些吃力，那建议你看下我的第一次总结：

      http://blog.csdn.net/xueyingxue001/article/details/51374100

 

EM算法处理的情况

      EM算法需要处理样本中含有隐变量的情况，什么意思？

      一般我们面临的问题是：对于一个函数f(x; θ)，里面x是已知的，但 θ未知，于是使用极大似然估计求 θ，但如果x是由(x, z)两部分组成，其中x已知z未知，也就是说样本中含有隐变量z，对于这种情况极大似然估计就没辙了，而为了解决这样的情况而发明的算法之一就是EM算法。

EM算法的缺点

      只能得到局部极值点，不能得到全局极值点。

      比如：给出男女身高样本，求男女身高分布。如果男性身高均值是1.80，女性1.65，那用EM算法求得的结果还是很不错的，但如果男性1cm，女性10m，那结果一定会和实际差太远。

K-means与EM

      这两个都是能处理含有隐变量情况的样本，因为在给定样本的情况下K-means是可以将未标记的样本分成若干个簇的，但K-means无法给出某个样本属于该簇的后验概率。

      而EM算法可以给出后验概率。

极大似然估计的回顾

二线分布的极大似然估计

      例子：10次抛硬币的结果是：正正反正正正反反正正

      目标：找出与样本的分布最接近的概率分布模型。

       解：

           1，假设p是每次抛硬币结果为正的概率。

           2，根据实验结果建立函数：

                 P= pp(1-p)ppp(1-p)(1-p)pp = p⁷(1-p)³

           3，为了通用化，设进行N次独立试验，n次朝上，N-n次朝下，然后在第二步的基础上使用对数似然函数作为目标函数：

                 h(p)= f(n|p) = log(pⁿ(1-p)^N-n)

           4，对p求导后令导数等于0，求得参数p：

                 h’(p)= n/p - (N-n)/(1-p) = 0

                => p = n/N

           5，于是对这个例子来说，其最优解是p = 0.7。

高斯分布的极大似然估计

      1，高斯分布的概率密度函数：

          

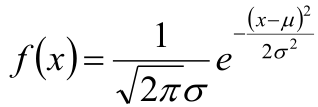
      2，将Xi 的样本值xi 带入，得到：

          

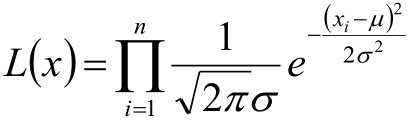
      3，取对数得到对数似然函数：

          

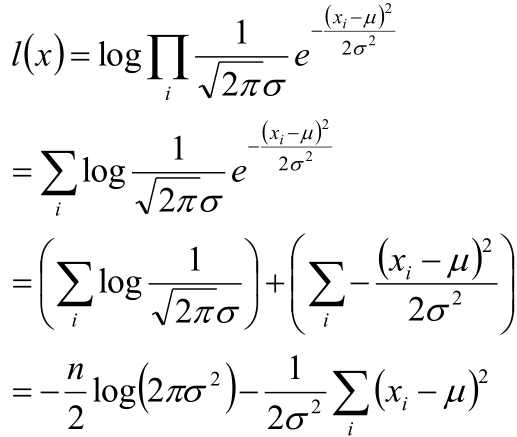
      4，目标函数确定：

          

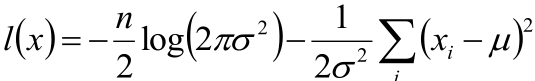
      5，将目标函数对参数μ,σ分别求偏导，得到μ,σ的式子：

          

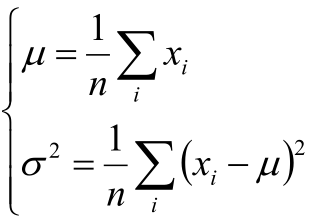
      6，可以看到利用极大似然估计求出的“样本的均指方差”就是“高斯分布定义的均指方差”。

EM算法

      首先先看个例子：

           随机挑选10000位志愿者，测量他们的身高：若样本中存在男性和女性，身高分别服从N(μ1 ,σ1 )和N(μ2 ,σ2 )的分布，试估计μ1 ,σ1 ,μ2 ,σ2 。

      这里的难点是什么？难点是：我们不知道哪些数据是男性的哪些是女性，如果知道的话就简单了，利用极大似然估计就OK，关键是不知道，于是这就是个含有隐变量的参数估计问题，这就要用到EM算法。

EM算法的思想

      首先还是给出题目：

           假定有训练集{x⁽¹⁾, x⁽²⁾, …, x^(m)}，包含m个独立样本，希望从中找到该组数据的模型p(x,z) 的参数，这里z是模型的隐变量。

      然后还是老样子写出对数似然函数：

          

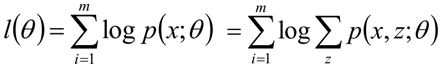
      接下来就是高斯式解释了，注意看：

          

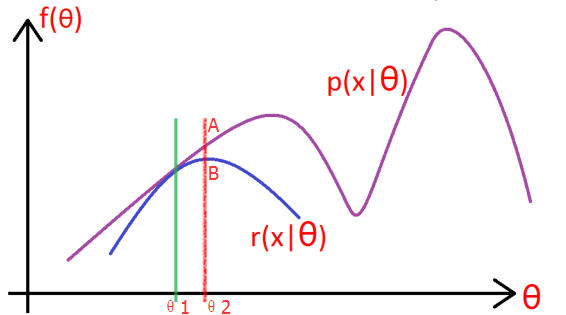
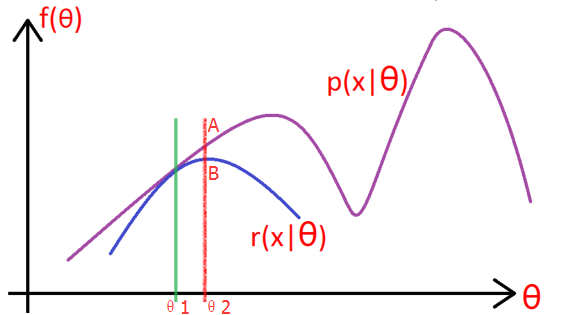
          如上图所示，紫色的线是我们的目标模型p(x| θ) 的曲线。

                    1，        因为这个模型含有隐变量z，所以为了消除z的影响，就先做一个除了不含有z模型：r(x| θ)，使得r(x| θ) ≤ p(x| θ)。（你先别管这个r怎么得到，方法之后会说，反正总能给一个r满足这个条件吧！），取一个值令 r(x|θ1) = p(x|θ1)，如绿线所示，然后对r(x| θ) 求极大似然，得到r的极值点B，和此时r的参数 θ2，如红线所示。

                    2，        这一步上图没有给出，就是：将r的 参数从θ1变成θ2，此时r的图像就向右上方移动，与p相交于A，此时仍然有r≤p。

                    3，        重复第二步和第三部，知道收敛。

          PS：从上图可以看出，EM算法只能求得局部极值点。

EM算法的欧拉式解释

欧拉式的解释就是：道理上能说得通，不过分讲究数学过程。 打个不太恰当的解释：     我说“生男生女的概率一样，但是如果连着生的话很有可能一个是男孩一个是女孩”(我所知的凡是有两个孩子而且两个孩子出生间隔不多的都是这样)     我也不知道为什么，也许这是个特例，但是对于我身边的人来说这就是个规律，可能这在医学上有严格的缘由，但抛开缘由，我上面的话也解释了如何生两个孩子一男一女。         于是，对于“如何生两个孩子一男一女”这个事情，严格的表述是“医学上有严格的缘由”，对应到机器学习这就是“高斯式的解释， 即严格的数学过程”，而“生男生女的概率一样，但是如果连着生的话很有可能一个是男孩一个是女孩”这个就是个欧拉式解释。 注1：这个仅是我身边的人是这样，可不是一定有这样的结果。 注2：即使是欧拉式的解释，也是需要有一定的根据的，我这个例子仅仅是我观测到的现象，仅仅用于让你理解什么是欧拉式解释。

          

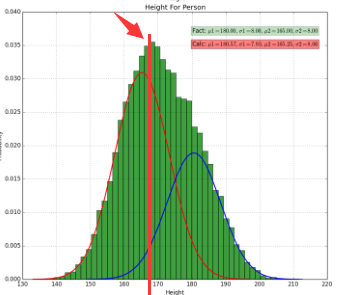
      对于上面的例子，如上图箭头所指位置可以看出：随机变量X是由两个高斯分布混合而成(男性的高斯分布和女性的高斯分布)

      为了通用性，假设一共有K个高斯分布，于是随机变量X是有K个高斯分布混合而成，取各个高斯分布的概率为π1 π2 ... πK ，第i个高斯分布的均值为μi ，方差为Σi。而目标也就变成：若观测到随机变量X的一系列样本x 1 ,x 2 ,...,x n ，试估计参数π，μ，Σ。

      PS：

           如果X是单变量的话，那要求的 μ 就有K个，即 μ = (μ1, μ2, ..., μk)

           如果X是N维的，那 μi就是N维的，那 μ 就是k个N维的数据，而 Σi 就是一个N*N的对称方阵，于是 Σ 就是K个N*N的方阵。

      根据上面的信息，建立对数似然函数：

          

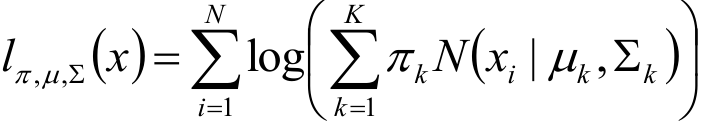
      解释：

           N(....)部分：xi发生的概率在一个均值和方差分别为μk 和 Σk 的高斯分布中。

           π_kN(....)：第k个高斯分布*被选中的概率

           (求和符号) π_kN(....)：所有的高斯分布混合起来

           (求和符号)log(后面一大堆)：本来对于所有的样本应该是：(连乘符号)* (求和符号) π_kN(....)，但是取了对数，于是变成了最终的样子。

       难题：

           xi知道，但是 π_k 不知道(我不知道哪些是男性哪些是女性啊)

       解决方法：

           1，估算数据来自哪个组份

                 估计数据由每个组份生成的概率：对于每个样本xi ，它由第k个组份生成的概率为

                

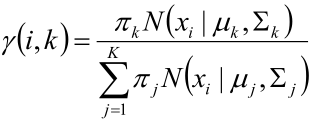
                 解释：假设有两个高斯分布，于是K=2，因此

                      k=1时代表xi属于第一个高斯分布的概率

                      k=2时代表xi属于第二个高斯分布的概率

           2，估计每个组份的参数

                 对于所有的样本点，对于组份k而言，可看做生成了这些点。

                 而组份k是一个标准的高斯分布，所以利用上面的结论，有：

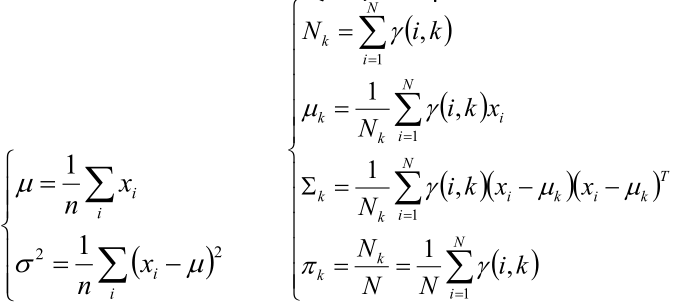  图1

                 解释：

                     对于如下样本：

                       身高为1.90的男性有0.9个，女性有0.1个，即：

                            总身高男性为1.90 * 0.9，女性为1.90 * 0.1

                      身高为1.81的男性有0.8个，女性有0.2个，即：

                            总身高男性为1.81 * 0.8，女性为1.81 * 0.2

                      ....

                     令k=1代表男性，k=2代表女性

                     于是

                      N_k：N_k=1 代表有多少个男性，N_k=2代表有多少个女性。

                            eg：N_k=1 = 0.9+0.8+....

                           π_k：π₁=男数/总数，即男数的先验概率，女同理。

                      μ_k：男性均值和女性均值。

                      ∑_k：男性方差和女性方差。

           3，循环上面两步，直到收敛。

                 Q：等等等等，上面两步第二步先不说，第一步的μk 和 Σk和πk我压根就不知道好吧，μk 和 Σk是待求参数，πk是隐变量，第一步都出不来，你让我怎么循环上面两步？

                 A：别急，我还没说完呢。

                 就好像对于投硬币问题，即使这个硬币是动过手脚以至于正反面的概率不一样，那我也可以：

                      a，根据先验知识猜“正面向上的概率是0.5”

                      b，通过大量的实验来不断调整这个概率

                      c，最后接近最真实的概率。

                 这个过程一样。

                 假设这里只有男女两个高斯分布：

                 于是EM算法就是：

                      a，根据先验知识先猜一个μ1，σ1，π1和μ2，σ2，π2，这样就得到了男女的高斯分布，这样第一步“估算数据来自哪个组份”就完成了。

                      b，将第一步的结果代入第二步求出新的μ1，σ1，π1和μ2，σ2，π2，然后把新的μ1，σ1，π1和μ2，σ2，π2代回第一步。

                      c，重复上面两步直到收敛。

      这就是EM算法的欧拉式解释。

      嘛，可能你还会有很多疑问，比如：为什么我不停的求出新的μ1，σ1和μ2，σ2就能不断接近最真实的情况呢？这些会在下面进行说明，总之这里先对EM算法的过程有更进一步的印象就达到目的了。

EM算法的高斯式解释

      首先是一个式子，如下：

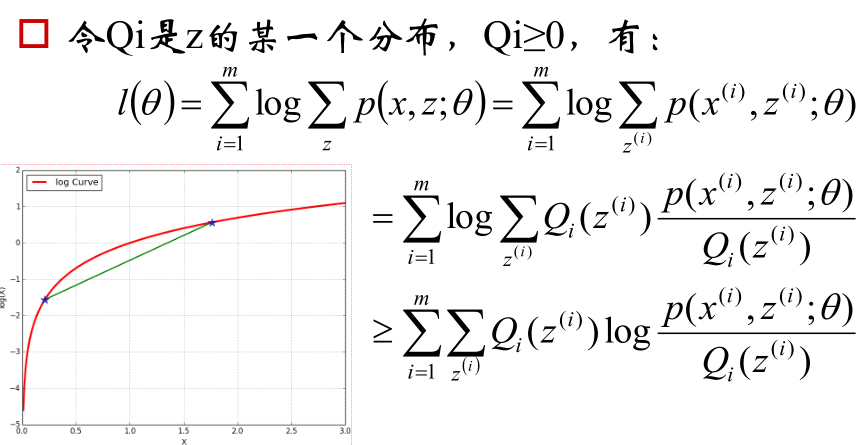图2

            PS：上图中的p(x⁽ⁱ⁾, z⁽ⁱ⁾; θ)/Q_i(z⁽ⁱ⁾) 是绿色的线。

      这个式子可以用Jensen不等式解释，不明白的看看我总结的Jensen不等式。

      为了方便说明，把上图中的最后的最后一个式子记为r(θ)，即r(θ)为：

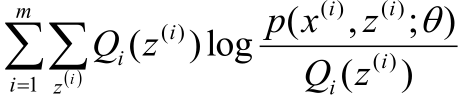              式1

      解释，上面的l(θ)是原目标函数的对数似然函数函数，而上式就反映了一个情况：原目标函数是有一个下界的，还记得下面这张图吗？

              

      于是图2中的式子就是反应：l(θ) = p(x|θ) ≥式1，话说，还记得“EM算法的思想”中的黑体部分的疑惑吗，即：这里的r(x|θ) 是什么？

      现在就能给出答案了：r(x|θ) 就是r(θ)，即式1。（为啥？因为EM算法的思想不就是找出一个r(x|θ) 使得p(x|θ) ≥ r(x|θ) 吗？而式1就满足这个要求）

      此时，“EM算法的思想”中的式子就可以补全了，即：

        l(θ) = p(x|θ) ≥ r(x|θ) = r(θ)

      接下来就简单了：

            1，        p(x|θ) = r(x|θ) 时的r(x|θ)。

            2，        求r(x|θ) 的极值点B。

            3，        重复上面两步直到收敛。

      但，又出现问题了(问题真是一个接一个啊)，即：上面的第一步怎么求？

      是这样。

      首先，先缩小问题范围，第一步的p(x|θ)，我们可以先根据先验知识给出一个θ，这样p(x|θ) 是已知的，而r(x|θ) 是式1，可式1中包含Q_i(z⁽ⁱ⁾)，因为Q_i(z⁽ⁱ⁾) 是隐变量z的一个分布，这个还不知道，所以只要想办法表达出Q，那第一步就解决了。

      于是，下面是说明如何求Q。

      还是图2，为了方便说明，令绿线和红线相交的两个点分别是x1和x2，由图2可知，为了让p(x|θ) = r(x|θ)，需要让x1和x2合并成一个点，而p(x⁽ⁱ⁾, z⁽ⁱ⁾; θ)/Q_i(z⁽ⁱ⁾) 是绿色的线，所以只有p(x⁽ⁱ⁾, z⁽ⁱ⁾; θ)/Q_i(z⁽ⁱ⁾) 等于一个定值时，绿色的线才能变成一个点，于是有下面的式子：

        p(x⁽ⁱ⁾, z⁽ⁱ⁾; θ)/Q_i(z⁽ⁱ⁾) = c

      于是还记得Q_i(z⁽ⁱ⁾)是什么意思吗？对，Q_i(z⁽ⁱ⁾)是隐变量的分布，而这个分布是什么？

      这就要回到最初的问题了：对于男女身高的问题，我们知道所有的身高数据，却不知道哪些数据是男性哪些数据是女性，在这样的情况下要求求出男女身高的分布。对这个问题“某个身高下：男性人数或者说男性所占的比例以及女性人数或者说女性所占的比例”就是隐变量z的分布，即：

        Q_i=男(z^(i=男))  = 男性人数/总人数

        Q_i=女(z^(i=女))  = 女性人数/总人数

      而“某个身高下，某个性别的人数”是什么？是p(x⁽ⁱ⁾, z⁽ⁱ⁾; θ)啊，因为如下图所示：

             

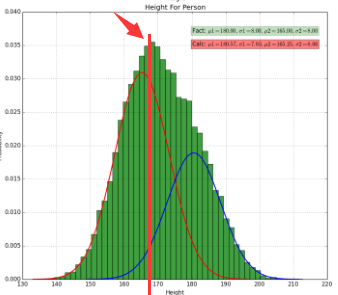
      某个性别的身高分布就是蓝线和红线，也就是p(x⁽ⁱ⁾, z⁽ⁱ⁾; θ)，如上图的红色竖线所示，我随便给个身高时p与红色竖线的交点就是“某身高下，某性别的人数”！

      进一步：“总人数”就是

             

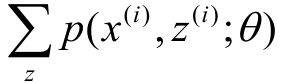
      也就是p(x⁽ⁱ⁾, z⁽ⁱ⁾; θ)/Q_i(z⁽ⁱ⁾) = c的c。

      现在一切都明了了，Q就是下式：

             

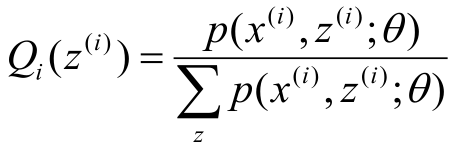
      不过这个式子挺繁琐的，因此使用如下推导进行简化：

             

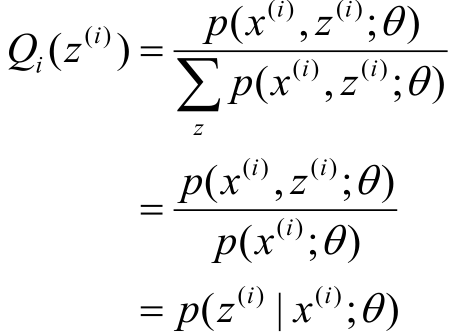
      得到结果：

             

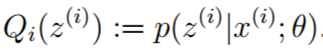
      即：Q是在给定参数θ和样本x时，隐变量z的条件概率。

EM算法的整体框架

      到此，EM算法的所有推导均以给出，于是结论也就出来了，如下图所示：

      

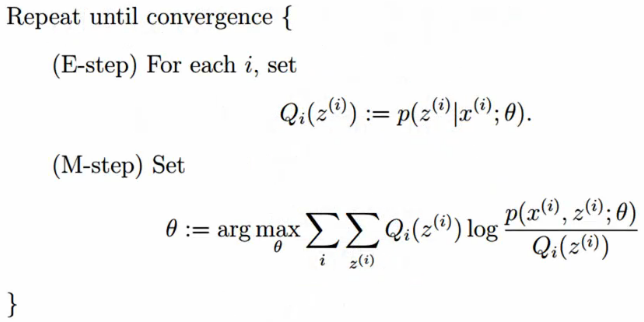
      E步(第一步)：

如果是首次运行，则根据先验知识给定一个θ；如果不是，则这个θ就是M步求出来的。

利用这个θ和样本x，求出隐变量z的条件概率，即Q。

      M步(第二步)：

           将E步求出的Q带入式1后求出θ的最大值。

      重复上面两步，直到收敛。

PS1：   几乎所有的教程都是说：E步是求期望，M步是在E步的基础上求最大化。   但，E步是求期望？骗鬼呢啊！   E步仅仅是求隐变量z的条件概率，M步才是既求期望(两个求和符号后面那一坨是期望，如果看不懂那你的复习高数了)，又求最大化好吧！   也不知道因为啥，大家都“睁着眼睛说瞎话”，愣说“第一步是求期望，并称呼为Expect步，第二步是求最大化，并称呼为Max步”，结果本来能说清楚的都解释不清楚了。明明第二步才是EM步：既求期望，又求最大化。 PS2：   M的公式可以写成： argmax_θ(求和_i)(求和_z(i))( Qi(z(i))log p(x(i), z(i); θ) - Qi(z(i))log Qi(z(i)))   因为Qi(z(i)) 是E步已经求好的，所以上式的Qi(z(i))log Qi(z(i))可以舍去，即：        argmax_θ(求和_i)(求和_z(i))( Qi(z(i))log p(x(i), z(i); θ) ) 式2   于是式2和M步是等价的，用哪个都行。

EM算法的统一的式子

      把Q步的结论带入式2，就得到了“使用一个式子表示的EM算法”，即：

           

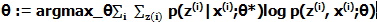
           PS：θ*是已经估计出的值，θ是待求的。

      如果在看我这篇总结之前，你已经看了很多教程，那上面的式子你应该不会陌生，而上面的式子其实就是用一个式子表示EM算法的两步，仅此而已。

      于是，用这个式子来说明EM算法的话就是：

           第一步：

如果是第一次，则根据先验知识给出一个θ*，如果不是第一次则 θ* 就是第二步求出的 θ。

           第二步：

根据已知的 θ* 求出一个更好的 θ。

           第三部：

                 迭代上面两步，直到收敛。

例子：从EM理论公式推导高斯混合模型

      随机变量X是有K个高斯分布混合而成，取各个高斯分布的概率为φ1 φ2 ... φK ，第i个高斯分布的均值为μ i ，方差为Σi 。若观测到随机变量X的一系列样本x1 ,x2 ,...,xn ，试估计参数φ，μ，Σ。

      解：

      E步：

            先写出E步的公式，如下：

                  

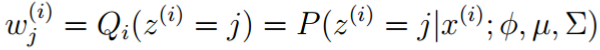
            现在知道了，E步这个公式就是第i个样本属于第j个高斯分布的概率，于是这个概率就是“EM算法的欧拉式解释”的这个式子：

                  

           这里只需要把上式中的 π 换成 φ 就好。

      M步：

           将多项分布和高斯分布的参数带入：

            

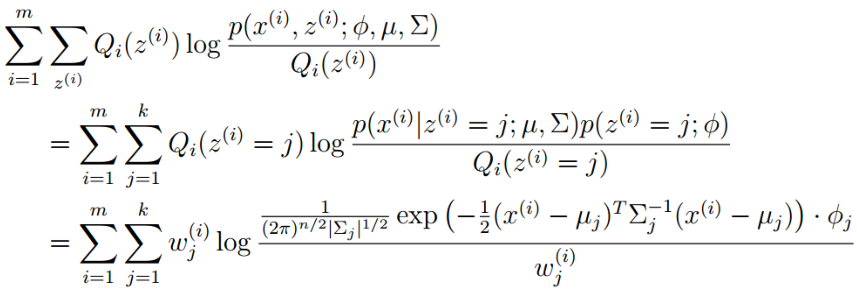
      解释：

            第一个等号：利用条件概率；

            第二个等号：

                  p(x⁽ⁱ⁾|z⁽ⁱ⁾=j; μ,Σ)是在给定组分j时x⁽ⁱ⁾的概率密度，于是直接带入高斯分布概率密度的公式。

                  p(z⁽ⁱ⁾=j; φ)是第i个样本属于第j个组分的先验概率，于是就是φ_j。

      下面就是对上式求偏导并令偏导为0：

      μ的偏导：

      

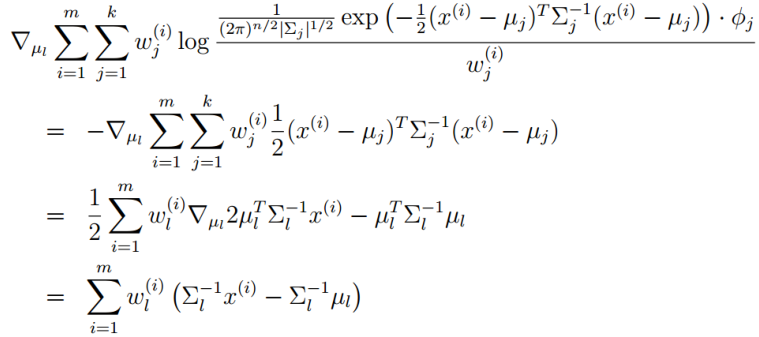
                 令上式 = 0，得：

                  

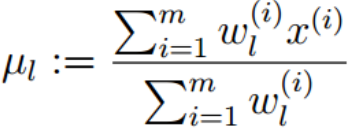
                 比如：1.85米时，此人属于男性的概率是0.8，属于女性的概率是0.2，于是x⁽ⁱ⁾=1.85，若l=男，则w⁽ⁱ⁾_l=男= 0.8，分母就是所有身高下男性的概率的和，若l=女，则w⁽ⁱ⁾_l=女= 0.2，分母就是所有身高下女性的概率的和。

          

              Σ的偏导并令偏导为0：

                 这个就直接给结论了，即：

                  

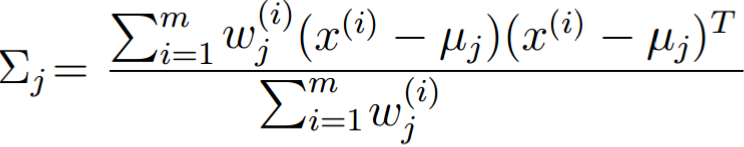
            φ的偏导：

                  考察M步的目标函数：

            

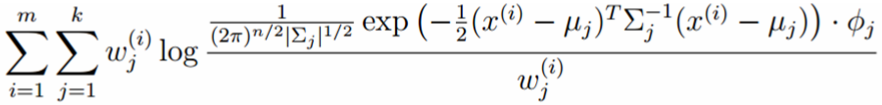
                  删除和φ无关的项：

                     

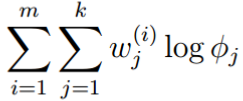
                  因为φ有个约束条件，即：所有φ的和为1，所以需要使用拉格朗日乘子法：

                        

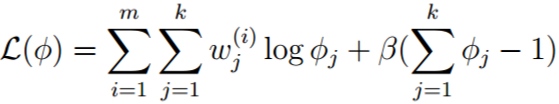
                  求导：

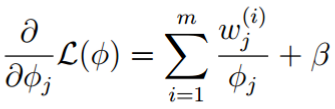                        式3

                 因为所有φ的和为1，所以：

                       

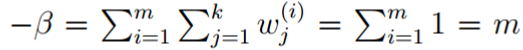
                 把上式会待到式3，得到：

                           

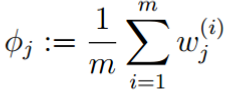
       总结：

              对于所有的数据点，可以看作组份k生成了这些点。组份k是一个标准的高斯分布，利用上面的结论：{γ(i,k)x_i | i = 1, 2, …, N}

                  

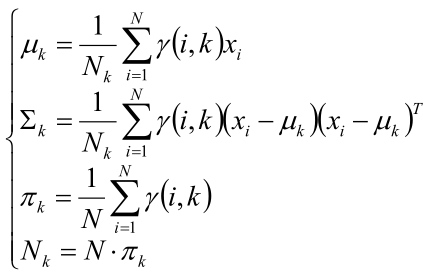
      这个结论和“EM算法的欧拉式解释”的结论是一样的！

代码（源自邹博老师）

      

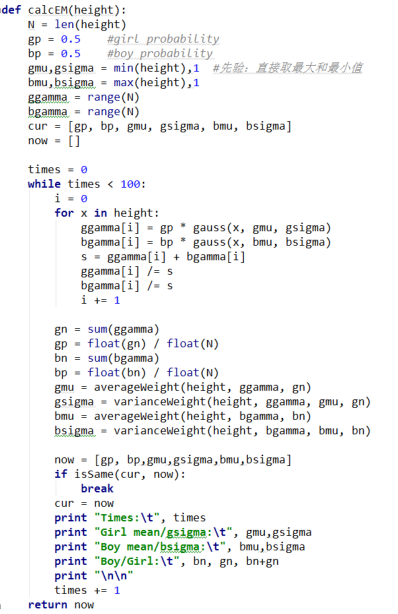
最后

以上就是追寻冰棍最近收集整理的关于EM算法再次总结EM算法处理的情况EM算法的缺点K-means与EM极大似然估计的回顾EM算法代码（源自邹博老师）的全部内容，更多相关EM算法再次总结EM算法处理内容请搜索靠谱客的其他文章。