概述
二次规划算法
对于道路边界线也需要求再sl坐标系下的l值，并且是离散的计算，这个离散的程度是和之前二次规划得到的粗解的离散是对应的（话说这个离散是和当时撒点的匹配还是评价五次多项式的时候取的离散的点？ 撒点的，五次多项式评估的时候稠密算cost只用于算，虽然后面算出之后有稠密了，这只是为了决策结果的详细性）
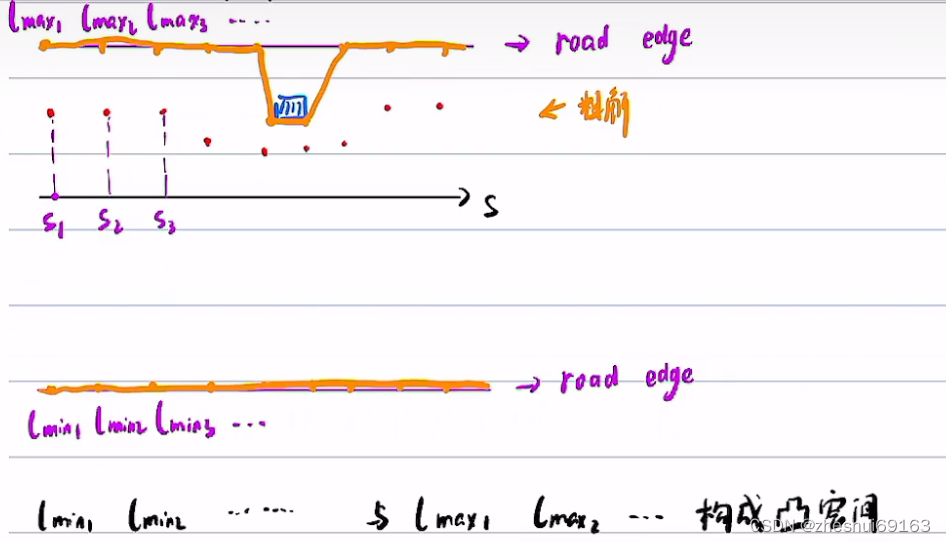
上图的 l_min 是已经考虑了障碍物的黄色，那把障碍物搞出去的线是咋确定的？（哎呀，这个就因为离散点，所以只用在粗节上找到那两个障碍物边界点的匹配点就行了，然后让粗解的这几个点的上界/下届关于障碍物坐标变化就行） 考虑了 l_min max则就把障碍物考虑过了，后面考虑其他损失因素
分段加速度是要干嘛？？？？？？？？
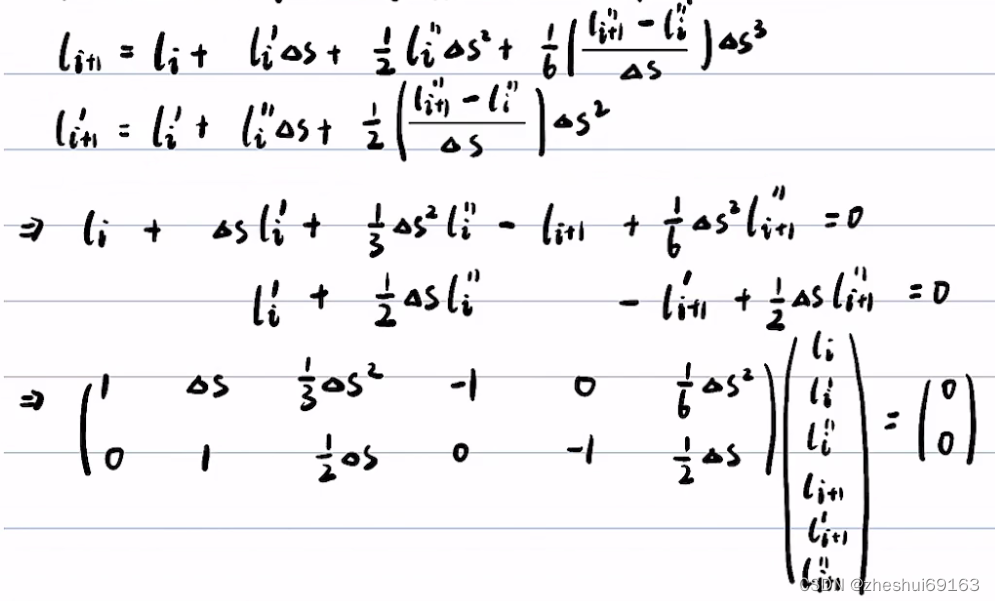
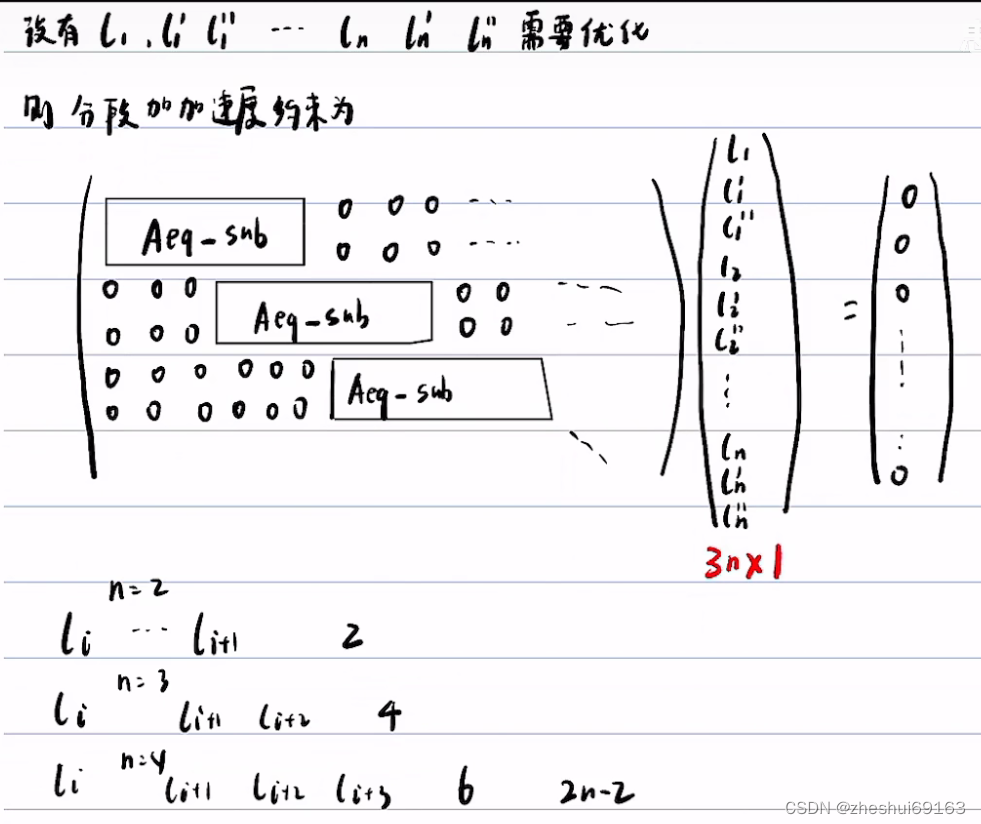
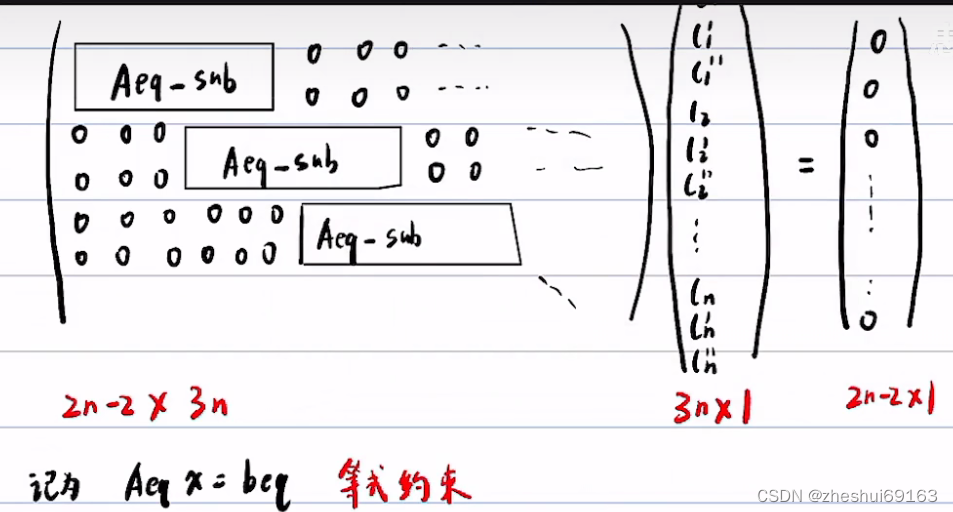
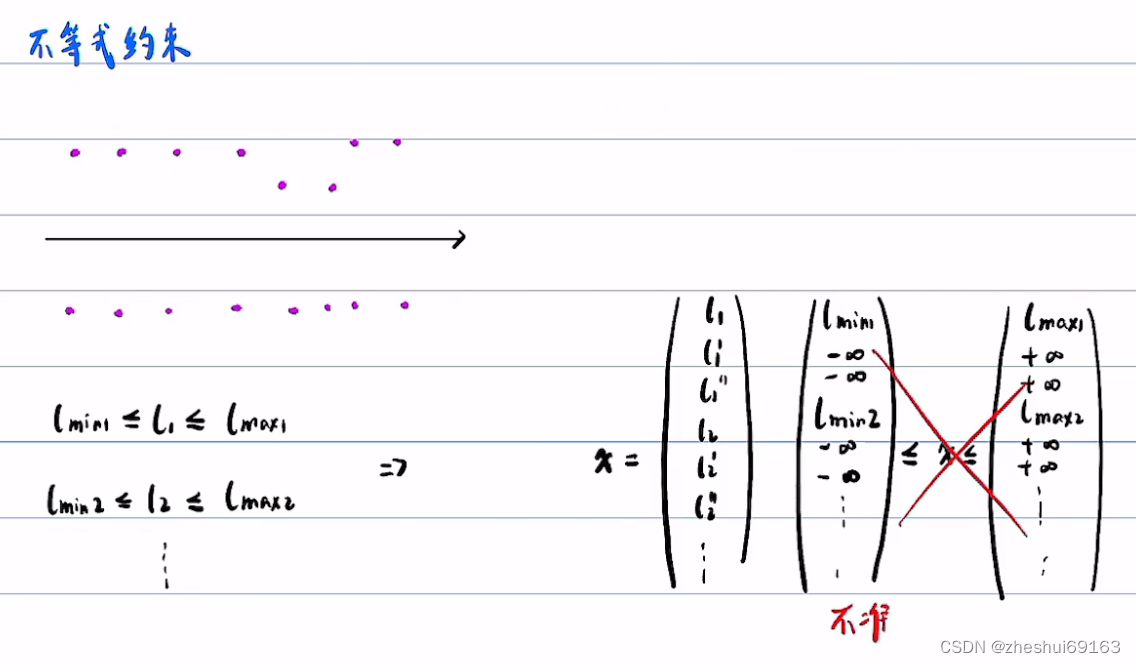
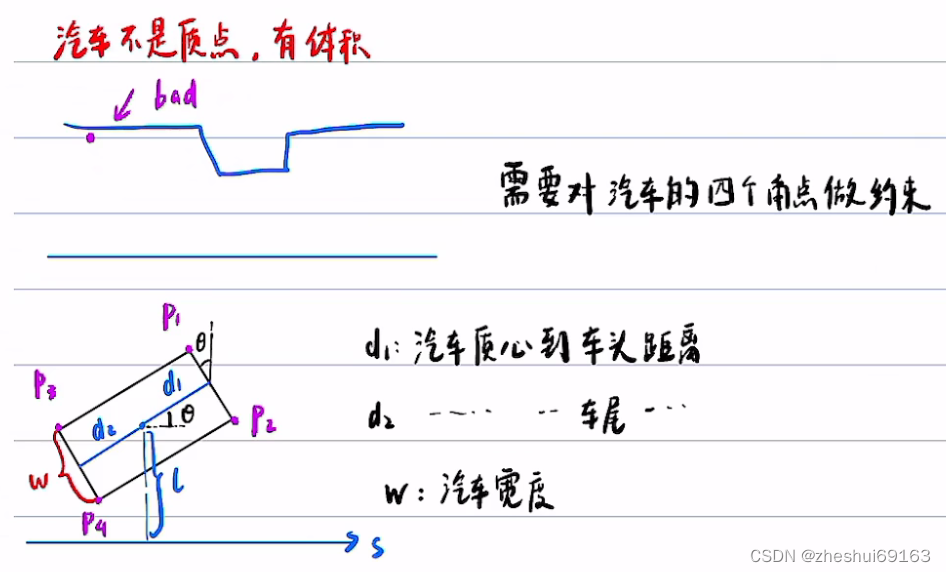
这是一种保守近似，因为把sin当作tan，相当于变大，把cos当作1，相当于变大，这样p1的 l 坐标变大，p2的l坐标相当于除以cos，再让xx，p2p3坐标大小如何变？？？？？？？？？？？？，p4坐标变小 注意：tan=l’ 这样就变换过来了
若直接如下图，让p1点的l坐标属于这个范围是不合适的，因为只考虑质心点所对应的 l_max_i 和 l_min_i 的话，而此时车头的p1所对应的并不是 l_max_i 和 l_min_i
所以要做的保守一些，如下：
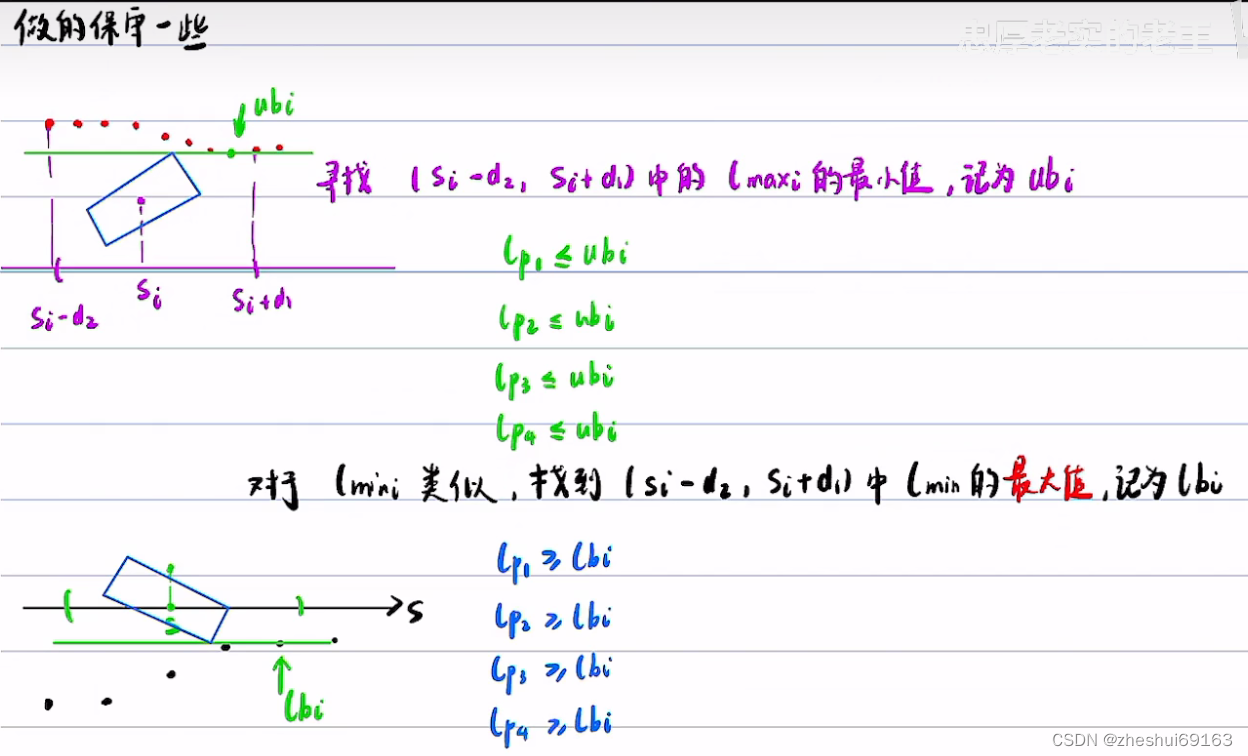
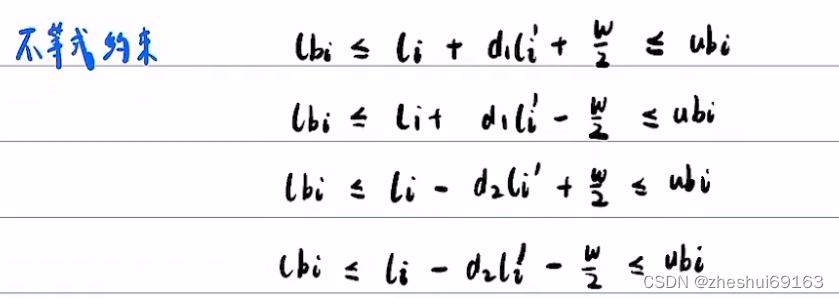
写成矩阵的形式，并让>=乘以-1，使得变为<=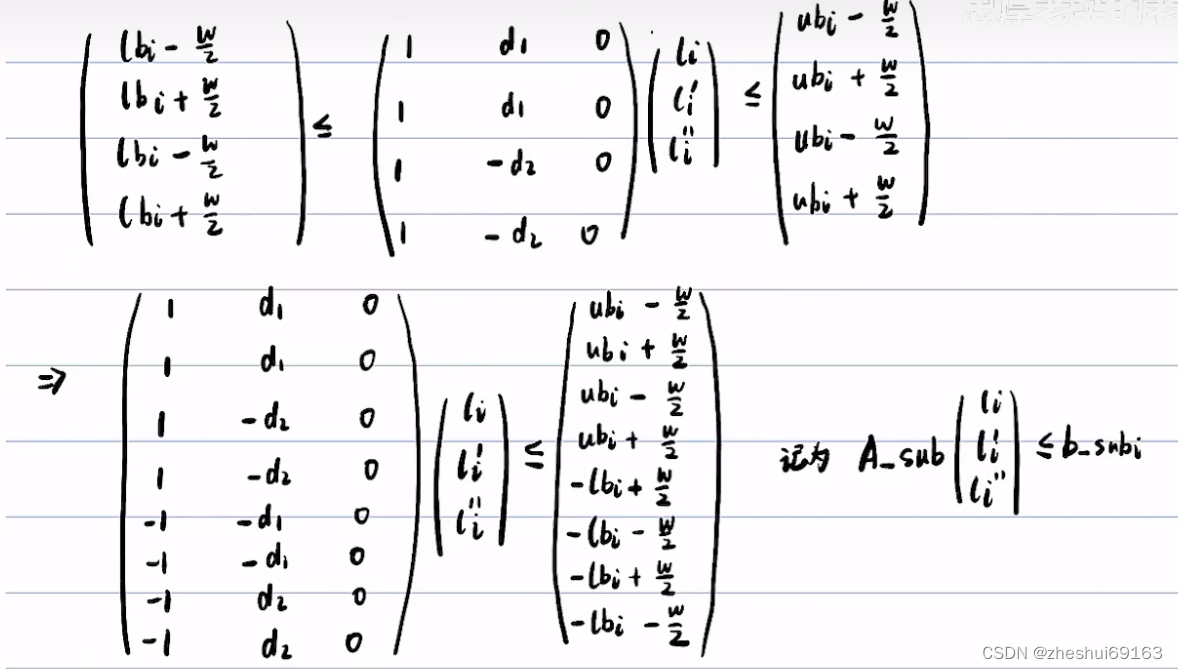
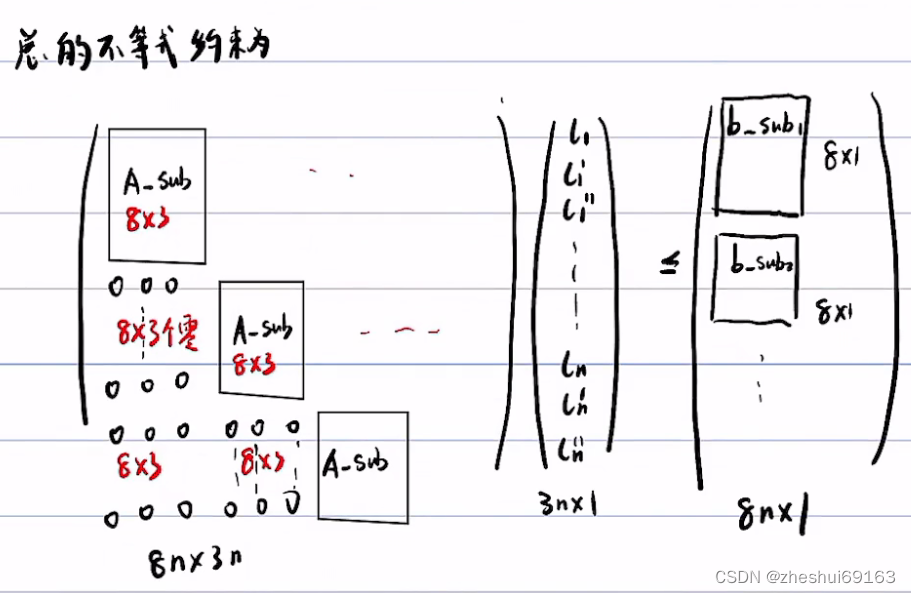
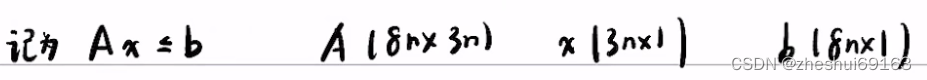
则总的二次规划的代价函数和约束如下
最后
以上就是沉静樱桃为你收集整理的第二章第四节(中) 路径二次规划算法二次规划算法的全部内容，希望文章能够帮你解决第二章第四节(中) 路径二次规划算法二次规划算法所遇到的程序开发问题。
如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。
发表评论 取消回复