0-1整数规划的LINGO求解

60 阅读 0 评论 40 点赞

我是靠谱客的博主无私悟空，最近开发中收集的这篇文章主要介绍0-1整数规划的LINGO求解，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

1.LINGO的简介

LINGO是由美国LINDO公司推出的求解优化模型的软件，对于求解线性、非线性和整数最佳化模型这类运筹学方面的问题，LINGO是一个很好的工具。官方提供免费试用版，可以在其官网下载www.lindo.com,当然，试用版能求解的问题规模会受到限制。LINGO求解优化问题需要用其特定的语法，但比较简单，对不同类型的模型可以很容易在网上找到相关的例子，LINGO对优化问题提供的命令能简化很多计算工作量，不需要用数值方法写大量代码，也不需要MATLAB那样不太易懂的语句。

2.0-1整数规划实例

有一个工厂生产的商品需要向n个经销商供货，向各地的经销商供货是通过配送中心，商品的物流为工厂 -> 配送中心 -> 经销商，现要选址确定配送中心，现有m个备选的配送中心，需要从备选的配送中心确定若干个，保证总的配送费用最低。

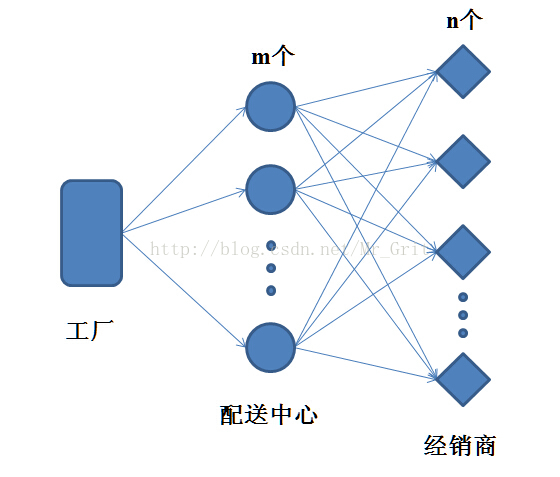
2.1 模型参数

2.2 建立优化模型

2.2.1 目标函数

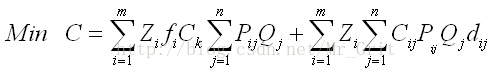
目标函数中共有两项：

第一项表示产品从工厂到各个配送中心的运输费用总和，

第二项表示产品从各个配送中心向经销商运输费用的总和。

2.2.2 约束条件

(1) 从m个配送中心选则m0个作为实际配送中心

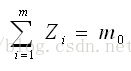
(2) 配送中心和经销商之间共有n对供求关系

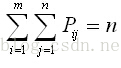
(3) 每个经销商只由一个配送中心进行供货

(4) 限定经销商的对应配送关系产生的前提是该备选配送中心已经被选中

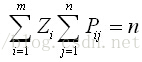
(5) 备选配送中心i只存在两种情况，当备选配送中心i被选中时取1，当备选配送中心i未被中时取0

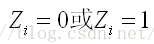
(6) 由工厂到各配送中心配送量之和等于各配送中心到经销商配送量之和

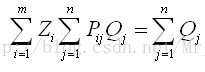
(7) 每个配送中心总配送量不超过允许的上限q0

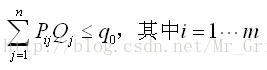
(8) 配送中心一定有其对应的配送客户，不存在物流配送中心被选中而没有客户的情况

(9) 当配送中心i向经销商j进行产品配送时值取为1，不向经销商j进行配送时取值为0

2.2.3 模型求解

在实例中需要从 m=13 个备选物流配送中心中选出最优的数量作为物流配送中心，同时确立每个配送中心与每个经销商的供货关系。模型中的参数 m =13，n = 209，从m个备选配送中心中选择 m0 个作为实际配送中心，m0 取值范围是 3-13 之间，并且假设运输费率中的 Cj 和 Cij 为常数 1。为了保证每个配送中心配送产品数量的均衡，设定每个配送中心的配送产品量最大值为1500，即 q0<=1500。

LINGO对模型求解：

这里给出了利用LINGO求解的代码，实际运行的代码可以下载：0-1整数规划的LINGO求解

<pre name="code" class="plain">model:
title LiZm;
sets:
! f：工厂到配送中心距离，z：每个配送中心是否被选;
city/1..13/:f,z;
! Q:每个经销商需求量;
company/1..209/:Q;
! D:配送中心到经销商距离，P：配送关系;
link(city,company):D,P;
endsets

data:
f=196 1305  1887  1280	1805	1211	1178	856	1365	274	16.3	1281	1409;
! 每个经销商的需求量，总共209个，没有全部列出，实际运行的代码需给全数据
Q=1.6010    2.3920    3.3500    0.6670    1.0350    5.0670    9.0470  159.6580    2.1580

! D为 209*13的矩阵，这里只列出了第一行
D=692	688	1599	1638	1239	1383	560	373	928	442	714	1638	1705 
enddata

! 对每个约束条件的定义
min=@sum(city(i):@sum(company(j):z(i)*f(i)*P(i,j)*Q(j)))
+@sum(city(i):@sum(company(j):z(i)*P(i,j)*Q(j)*D(i,j)));
@sum(city(i):z(i))=6;! m0自己设定;
@sum(city(i):@sum(company(j):P(i,j)))=209;
@for(company(j):@sum(city(i):P(i,j))=1);
@sum(city(i):@sum(company(j):z(i)*P(i,j)))=209;
@sum(city(i):@sum(company(j):z(i)*P(i,j)*Q(j)))=@sum(company(j):Q(j));
@for(city(i):@sum(company(j):P(i,j)*Q(j))<=1500);
@for(city(i):z(i)-@sum(company(j):P(i,j))<=0);
@for(city:@bin(z));
@for(link:@bin(P));
end

从代码可以看出LINGO对于优化问题的求解是相当方便的，代码只需要目标函数 -> 定义变量 -> 约束条件，和建模过程一样，只需了解一些LINGO的语法就可以很容易求解。