15.异常检测 Anomaly detection

觉得有用的话,欢迎一起讨论相互学习~

吴恩达老师课程原地址
参考资料 斯坦福大学 2014 机器学习教程中文笔记 by 黄海广

15.1问题动机 Problem motivation

飞机引擎异常检测

• 假想你是一个飞机引擎制造商，当你生产的飞机引擎从生产线上流出时，你需要进行 QA(质量控制测试)，而作为这个测试的一部分，你测量了飞机引擎的一些特征变量，比如引擎运转时产生的热量，或者引擎的振动等等。如下图所示：$x_1,x_2,x_3...$ 用以表示测量得到的飞机引擎的特征。而数据集中的m个数据用$x^{(1)},x^{(2)},x^{(3)}...x^{(m)}$表示
• 这样一来，你就有了一个数据集，从 $x^{(1)}到x^{(m)}$，如果你生产了 m 个引擎的话，你将这些数据绘制成图表，看起来就是这个样子：
  
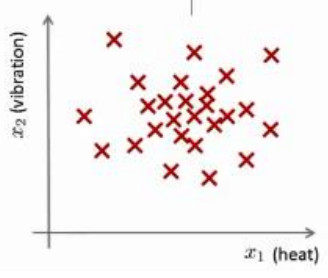
• 这里的每个点、每个叉，都是你的 无标签数据 。这样，异常检测问题可以定义如下：假设后来有一天，你有一个新的飞机引擎从生产线上流出，而你的新飞机引擎有特征变量$x^{test}$。所谓的异常检测问题就是：希望知道这个新的飞机引擎是否有某种异常，或者说，我们希望判断这个引擎是否需要进一步测试。因为，如果它看起来像一个正常的引擎，那么我们可以直接将它运送到客户那里，而不需要进一步的测试。
• 给定一个训练集，然后对训练数据进行建模即$p^{(x)}$,即对飞机引擎的特征进行建模，然后当给定一个新的数据即$x^{(test)}$,如果概率$P^{(test)}$低于阈值ε-- 那么就将其标记为异常，如果概率$P^{(test)}$大于等于阈值ε-- 那么就将其标记为正常
• 观察模型，将会发现在中心区域的这些点概率相当大，而稍微远离中心的点概率会少些，而离中心更远的点，其概率会更小即出现异常的概率会更大，而最外的标记点就是 异常点(anomaly) ,而中心区域的点P(x)很大即是 正确的点
  
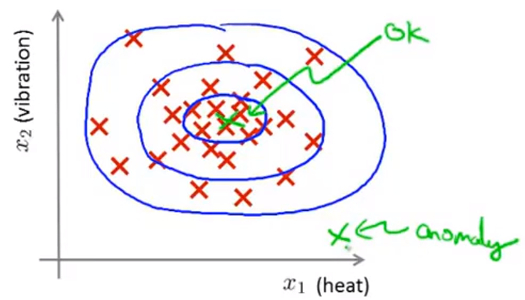
• 这种方法称为 密度估计 表达如下：
  $$ifp(x)\{\begin{array}{l}\le ϵanomaly\\ >ϵnormal\end{array}$$

欺骗识别

• 使用$x^{(i)}表示第i个用户的行为特征$，通过检测是否有$p(x)<ϵ$来断定用户是否是一个非正常用户。
• 异常检测主要用来识别欺骗。例如在线采集而来的有关用户的数据，一个特征向量中可能会包含如：$x_1$用户多久登录一次，$x_2$访问过的页面，$x_3$在论坛发布的帖子数量，甚至是$x_4$打字速度等。尝试根据这些特征构建一个模型，可以用这个模型来识别行为异常的用户。

数据中心异常检测

• 特征可能包含：$x_1$内存使用情况，$x_2$被访问的磁盘数量，$x_3$CPU的负载，$x_4$网络的通信量等。根据这些特征可以构建一个模型，用来是否有$p(x)<ϵ$来判断某些计算机是不是有可能出错了

15.2高斯分布 Gaussian Distribution

• 通常如果我们认为变量 x 符合高斯分布 x~N(μ,σ2)则其概率密度函数为：
  
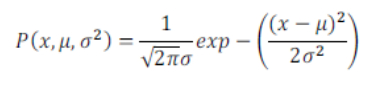
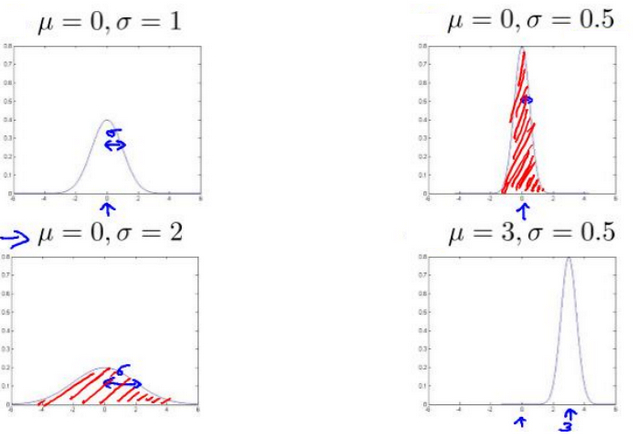
  其中$mu $表示数据的平均值而$sigma^2$表示样本的方差，横轴表示数据的值，而纵轴则表示此值出现的概率密度，图像与一段范围内的横轴包围的面积即为x的取值落在此范围内的概率，其图像如下图所示：
  

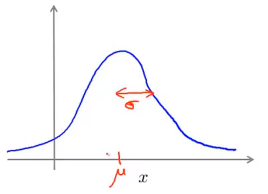
其中$\mu$控制图像的中线所在位置，而$\sigma$控制图像的宽度，并且对于概率密度函数而言，其与坐标轴包围的区域的面积始终为1

• 利用已有的数据来预测总体中的$\mu 和{\sigma }^2$的计算方法如下：
  
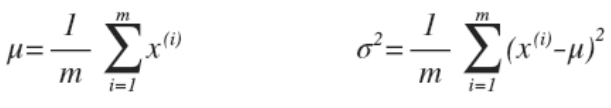
  其中统计学家认为计算方法中的分母应该为(m+1),而机器学习学者则认为其中的分母为m也很合适，当时数据量十分巨大时，分母为m或者为(m+1)实质上没有很大的区别。
  

15.3非监督学习的异常检测算法

• 假定有共m个样本的无标签训练集，训练集中的每个样本都是一个$R^n$维的特征向量。
  则处理异常检测的方法是 使用数据集建立起概率模型p(x) 试图通过特征量的乘积来对样本的异常状况进行检测。
• 假设特征量之间是相互独立的，则概率模型可表示为特征量的概率的乘积：$$P(x)=p(x_1)p(x_2)p(x_3)...p(x_n)$$
• 假设特征都是分散的，并且 服从高斯正态分布 则概率模型可表示为$$p(x)=p(x_1;{\mu }_1,{\sigma }_1)p(x_2;{\mu }_2,{\sigma }_2)p(x_3;{\mu }_3,{\sigma }_3)...p(x_n;{\mu }_n,{\sigma }_n)$$即$$\prod _{j=1}^{n}p(s_j;{\mu }_j,{\sigma }_j^2)$$

异常检测算法概述

1. 挑选对异常检测有用的特征$x_i$
2. 计算每个特征的均值和方差${\mu }_1,{\mu }_2,u_3...,{\mu }_n,{\sigma }_1^2,{\sigma }_2^2,{\sigma }_3^2...{\sigma }_n^2$
   
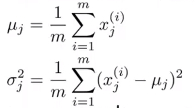
3. 给定样本x,计算概率p(x),$如果概率小于ϵ$,则判断这个样本存在异常
   

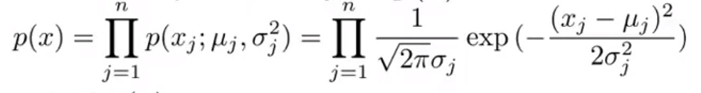
异常检测示例

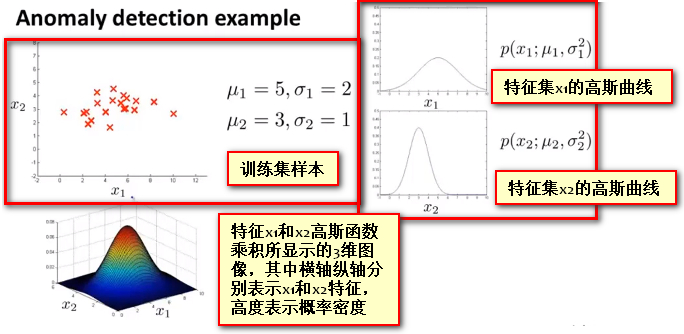
• 此时选定$ϵ$大小为0.02，则计算样本点$x_{test}^{(1)}$的概率为0.0426，而计算样本点$x_{test}^{(2)}$的概率为0.0021。因此样本1可以被视为正常样本，而样本2则被视为异常样本。

最后

以上就是健壮滑板最近收集整理的关于[吴恩达机器学习笔记]15.1-3非监督学习异常检测算法/高斯回回归模型15.异常检测 Anomaly detection的全部内容，更多相关[吴恩达机器学习笔记]15.1-3非监督学习异常检测算法/高斯回回归模型15.异常检测内容请搜索靠谱客的其他文章。