随机向量x的协方差阵_从线性变换的角度看高斯分布协方差阵的意义

109 阅读 0 评论 72 点赞

数学真的是很奇妙，在独立的课程中学习到的知识，有时候很难联系起来，但是实际上它门之间有着紧密的联系，今天就谈一点自己关于矩阵与高斯分布的关系，也是在拜读了很多大咖的文章之后才有了一些更深的理解。

1、矩阵与线性变化的关系。矩阵是线性代数中的重要概念，实际上每一个矩阵都对应着一个线性变换。线性变换指的是对空间中的向量进行旋转和伸缩两种直观的操作。一个矩阵基本上就融合了这两种操作。

2、矩阵与高斯分布的关系。多元高斯分布由均值和协方差矩阵决定。协方差矩阵是典型的实对称矩阵。方差又是衡量高斯分布离散程度的统计量。

那么结合1和2，协方差矩阵对高斯分布而言，具有怎样的直观含义呢？

首先，有一个协方差矩阵为

，均值为[0,0]的二元高斯分布。对应的散点图大概为：

那我们从协方差的角度来看，这个协方差矩阵是对二元的标准正态分布做了怎样的变换得到的。

一个标准的二元高斯分布的散点图大概为这个样子

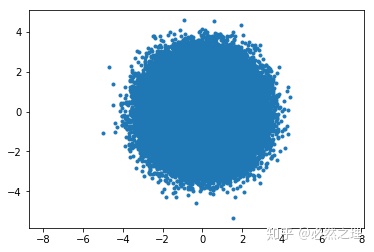
我们把协方差矩阵分解为

的形式，其中Q为标准正交基矩阵，D为对角阵。则有：

左乘的第一个矩阵

表示将标准高斯分布顺时针进行一个旋转操作，得到

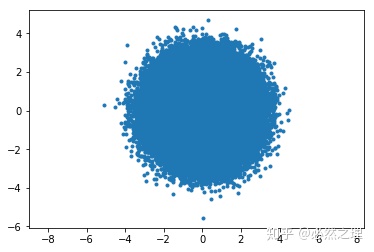
从图中看不出这个旋转操作对标准高斯分布有何明显的影响。

紧接着左乘的第二矩阵是对角矩阵，表示对旋转后的高斯分布进行横向的拉伸和纵向的压缩，需要注意的是，拉伸和压缩的幅度是标准差的单位，所以需要对对角阵的元素进行开方得到

，这样，高斯分布变成如下的形式：

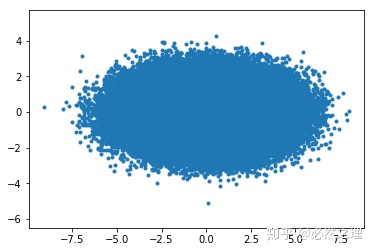
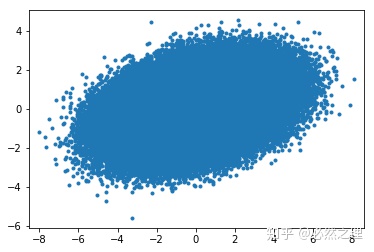
最后是左乘最后一个矩阵，表示对拉伸和压缩后的高斯分布进行相同角度的逆时针旋转，得到

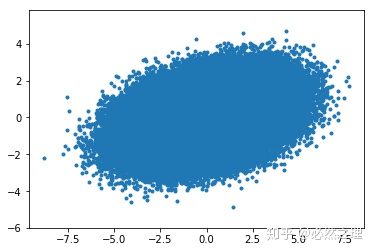
所以，经过这样一波操作，就得到了协方差为

的高斯分布。

从特征值和特征向量的视角来看，协方差矩阵是把标准高斯分布在特征向量的方向是进行拉伸和压缩。

本图文内容来源于网友提供，作为学习参考使用，或来自网络收集整理，版权属于原作者所有。