斯坦福大学机器学习笔记——异常检测算法（高斯分布、多元高斯分布、异常检测算法）

异常检测问题介绍：
异常检测算法主要用于无监督学习问题，但从某种角度看它又类似于一种有监督学习的问题，下面我们从一个例子中简单介绍一下什么是异常检测问题。
比如我们有一个飞机引擎制造商，对于一个新造出的飞机引擎我们想判断这个引擎是不是异常的。
假如我们有两个飞机引擎的特征：1）引擎运转时产生的热量；2）引擎的震动强度。我们得到了一个数据集：${x^{1},x^{2},...,x^{m}}$，绘制的关于特征的数据分布如下图所示：

这里的每个叉都是上述的无标签的样本。
异常检测的问题可以定义如下：对于给定的数据集${x^{1},x^{2},...,x^{m}}$，我们假使数据集是正常的，我们希望知道新的数据$x_{test}$是不是异常的，即这个数据不属于改组数据集的几率如何。我们所构建的模型应该能够根据预测数据的位置告诉我们其属于这一组数据的可能性$p(x)$。
这种方法称为密度估计，表达式如下：

其中，$p(x)$代表新来的样本$x$属于这一组数据的可能性。值得注意的是，我们假设数据集中的样本是正常的，也就是说对于我们原来的数据集，正常的样本应该占据很大的比例，这样用异常检测的效果才会很好。
异常检测的其他应用：
1.一些生产物件的异常检测（飞机引擎、家电等）；
2.可以用来识别欺骗。检测用户是否被盗号（通过用户的行为与之前行为的区别）。

高斯分布：
通过上述例子的解析我们知道了什么是异常检测，同时我们知道了对于异常检测算法来说，一个关键的问题是我们怎么对于给定的数据集进行密度估计得到$p(x)$。所以我们这一节介绍一种密度估计的方法——高斯分布。
我们先简单介绍一下什么是高斯分布，通常我们认为变量$x$符合高斯分布$xsim N(mu,sigma ^{2})$，则其概率密度为：

其中，$mu$和$sigma^{2}$（参数估计问题）可以通过下式获得：

对于上式，在不同$mu$和$sigma^{2}$下$p(x)$的形式如下：

值得注意的是：机器学习中求取方差时，我们除以m而不是像统计学中那样除以（m-1），其实对于除以m还是（m-1），当数据集的数量很大时，区别不是很大，但是机器学习领域的人都是习惯使用m。

异常检测算法：
下面我们结合异常检测问题以及高斯分布，给出异常检测算法的形式：
对于给定的数据集${x^{(1)},x^{(2)},...,x^{(m)}}$，每一个样本$x^{(i)}in R^{n}$，假设$x$服从高斯分布，即$x_{1}sim N(mu_{1},sigma _{1}^{2})、x_{2}sim N(mu_{2},sigma_{2} ^{2}),...,x_{n}sim N(mu_{n},sigma_{n} ^{2})$，我们对每一个特征（这里选择的特征是与异常具有相关属性的特征）计算$mu_{j}$和$sigma_{j}^{2}$：

获得均值和方差之后，对于给定的一个新的样本我们根据模型计算$p(x)$：

其中n为特征的数量。我们将$p(x)=epsilon$作为判定边界，当$p(x)<epsilon$则判断为该测试样本为异常样本；当$p(x)>epsilon$则判断该测试样本为正常样本。
以两个特征为例，看一下算法实现的形式：

上述的圆圈对应的是判定边界，不同的圆圈大小对应的不同的$epsilon$值，对于测试样本来说，如果测试样本的位置在圆圈内部为正常样本，在圆圈外部为异常样本。
对应的三维图表示形式如下，其中z轴为对应的特征取值的密度估计$p(x)$：

z轴的值高于圆圈对应的值为正常样本，低于圆圈对应的值为异常样本。

开发和评价一个异常检测算法：
上述我们讨论异常检测算法的实现方式，但是我们怎么对该算法进行评估呢？其实我们评价的方式类似于有监督方法的评估，虽然异常检测算法是一种无监督学习的算法，但是评估我们可以从一些带标签的数据入手，具体的评估方式如下：
我们从带标签的数据入手，用其中一部分正常数据用于构建训练集，然后使用剩下的正常样本和异常样本混合的数据构建交叉验证集和测试集。其中的比例分配为将正常数据的60%用于训练，构建训练集；用20%的正常数据和50%的异常数据构建交叉验证集；用20%的正常数据和50%的异常数据构建测试集。
评价的具体实现方法如下：
1. 根据训练集数据，估计出特征的均值和方差，然后构建出概率密度估计函数$P(x)$。
2. 对交叉验证集，我们尝试不同的$epsilon$值作为阈值，并预测数据是否异常，根据F1值或者查准率与查全率的比例选择最佳的阈值$epsilon$。
3. 选出最佳的$epsilon$后，针对测试集进行预测，计算异常检测算法的F1值或者查准率与查全率之比。

异常检测算法与监督学习算法的比较：
下面我们来比较一下异常检测算法和监督学习算法：
1. 对于异常检测算法来说，训练集中只有非常少量的正向类（异常数据），存在着大量的负向类（正常数据），即存在着数据类别的明显偏斜；而对于监督学习算法同时拥有大量的正向类和负向类样本。
2. 对于异常检测算法来说，异常可能会有很多种类，但是我们只需判断出异常即可，想要判断出异常的种类，对于只有少量的正向类样本的异常检测算法来说非常困难；对于有监督的算法，由于存在着大量的正向类样本，可以对正向类进一步的划分类型。
3. 对于异常检测算法来说，可以判断出未来不同的异常，也就是只要是异常，异常检测算法就可以判断出；但是对于有监督学习来说，对于未来不可知的异常，它是无法分类的。也就是说，对于异常检测算法，未来遇到的异常可能与已经掌握的异常非常的不同；对于有监督学习算法来说，未来遇到的正向类样本可能与训练集中的非常近似。
上述异常检测算法的不同之处，也就确定了什么时候我们使用异常检测算法，什么时候我们使用有监督学习的算法。

特征的选择：
对于异常检测算法，我们使用的特征是至关重要的，下面我们讨论一下怎么选择特征。
1. 对于异常检测算法来说，我们假设特征服从高斯分布，所以我们在进行异常检测之前，可以先画出样本的直方图（matlab使用hist命令），如果数据满足高斯分布，这可以直接得出$p(x)$，如果不满足高斯分布（也能够工作，只是调整之后效果会更好），可以将数据进行调整，使其满足高斯分布。调整的策略一般为：取对数（$x=log(x+c)$，$c$是一个实数）、取幂次（$x=x^{c}$，$c$是一个0~1的数）等方法。
2. 使用误差分析的方法调整特征或者增加特征。误差一般来自于一些异常的数据具有较高的$p(x)$值，我们可以分析那些被算法错误预测为正常的数据，观察能否找出一些问题。我们可能能从问题中发现我们需要增加的一些新的特征，增加这些新的特征后获得的新算法能够帮助我们更好地进行异常检测。
3. 我们也可以将一些相关的特征进行组合，来获得一些新的更好的特征（异常数据的该特征的值异常的大或者异常的小）。

多元高斯分布：
上述我们使用高斯分布建立的异常检测算法，有一个假设前提，那就是不同特征之间是不相关的。如果我们有两个相关的特征，而且这两个特征的值域范围比较宽，这种情况下，上述建立的高斯分布模型不能很好的识别异常数据。这时候我们需要建立多元高斯分布模型的异常检测算法以实现很好的异常检测。
下面简单的介绍一下多元高斯分布：
在一般的高斯分布模型中，我们计算$p(x)$的方法为通过分别计算每个特征的概率值$p(x_{j})$然后将其累乘，从而得到最终的$p(x)$。而对于多元高斯分布模型来说，我们将构建特征的协方差矩阵，用所有的特征一起计算$p(x)$。
计算过程如下：
1. 计算所有特征的均值，均值的计算方法过程如下：

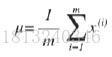
2. 利用上述获得的均值计算协方差矩阵，计算过程如下：

3. 计算多元高斯分布的$p(x)$：

下面我们看一下均值和协方差矩阵对模型的影响：

多元高斯分布模型与原高斯分布模型之间的关系：
原来的高斯分布模型是多元高斯分布模型的一个子集，从上面的三个例子1，2，3可以看出，这三个例子建立的多元高斯模型就是原来的高斯分布模型，也就是说只要多元高斯分布模型的协方差矩阵非对角线上的元素为0（即分布符合关于x轴以及y轴平行的直线对称——轴对齐），则多元高斯模型与原来的高斯分布模型是一致的。
下面我们来比较一下原来的高斯分布模型与多元高斯分布模型：
1. 原高斯分布模型不能捕捉特征之间的相关性，但可以通过将特征组合的方式实现；多元高斯分布模型能够自动的捕获特征之间的相关性
2. 原高斯分布模型计算代价小，能够适应于小规模和大规模的特征（例如$n=10000$）；而多元高斯分布模型由于在计算的过程中需要计算协方差矩阵的逆，当特征的数目很大时是非常耗时的，所以计算代价很高，不适应大规模的特征。
3. 对于多元高斯分布模型，需要有样本的数量m大于特征的数量n，否则协方差矩阵不可逆，通常需要$m>10n$，另外特征的冗余也会导致协方差矩阵不可逆；而原来的高斯分布模型在m很小的情况下同样适用。
下面我们来讨论一下协方差矩阵不可逆的情况以及解决的方法：
协方差矩阵不可逆也就是协方差矩阵是奇异矩阵，通常有两种情况产生：
1. 没有满足$m>n$。
2. 有多余的特征，也就是说可能两个特征是相同的或者有关联的（$x_{1}=kx_{2}$或者$x_{1}=x_{2}+x_{3}$）
解决方法：
对于1的情况，我们可以增加样本的数量；对于2的情况，我们应该找到相关的特征，去除多余的特征。

最后

以上就是健忘狗为你收集整理的斯坦福大学机器学习笔记——异常检测算法（高斯分布、多元高斯分布、异常检测算法）的全部内容，希望文章能够帮你解决斯坦福大学机器学习笔记——异常检测算法（高斯分布、多元高斯分布、异常检测算法）所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。