二元离散型随机分布

联合概率分布

$$P(X=x_i,Y=y_j)=p_{ij}$$

边际分布

$$P(Y=y_j)=\sum _{i=1}^N{p}_{ij}$$

二元随机变量的分布函数

联合分布函数(joint distribution function)

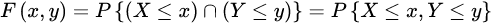
边际分布函数

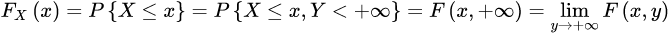
条件分布函数

在给定Y=Yj条件下X的条件分布函数为

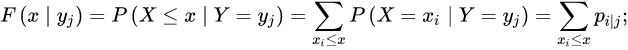
二元连续型随机变量

联合概率密度函数

概率密度函数的二元版本

边际概率密度函数

$$f_X(x)={\int }_{-\infty }^{\infty }f(x,y)dy$$

条件概率密度函数

$$f_x{|}_y(x|y)=\frac{f(x,y)}{f_Y(y)}$$

二元均匀分布与正态分布

1. 二元均匀分布的条件分布仍为均匀分布
2. 二元正态分布的边际分布是正态分布，并不依赖与参数ρ
3. 二元正态分布的条件分布是正态分布，与ρ相关

随机变量的独立性

$$F(x,y)=F_X(x)F_Y(y)$$与$$f(x,y)=f_X(x)f_Y(y)$$等价，即随机变量独立

定理：只要密度函数可以分解成两个函数的积，则随机变量X,Y必定独立

二元随机变量的函数的分布

Z=X+Y的分布

1. X与Y均为泊松分布，则Z=X+Y也为泊松分布，参数为λ1+λ2
2. X与Y均为正态分布，则aX+bY+c服从N(aμ1+bμ2+c,a²σ1²+b²σ2²)
3. Z=X+Y可以看成是Y被换成了Z-X，而Z相当于X,Y，是一个变量，只不过是由X,Y组成，求Z的密度函数实际上是求边际密度分布，只要积分即可（对X或者对Y积分都可以）
   $f_Z(z)={\int }_{-\infty }^{+\infty }f(z-y,y)dy$
   或者
   $f_Z(z)={\int }_{-\infty }^{+\infty }f(x,z-x)dy$

M=max{X,Y}, N=min{X,Y}的分布

1. Fmax(z) = P(X<=z,Y<=z)=FX(z)FY(z)
2. Fmin(z) = 1-(1-PX(z))(1-PY(z))

最后

以上就是聪慧蓝天为你收集整理的多元随机变量及其分布二元离散型随机分布二元随机变量的分布函数二元连续型随机变量随机变量的独立性二元随机变量的函数的分布的全部内容，希望文章能够帮你解决多元随机变量及其分布二元离散型随机分布二元随机变量的分布函数二元连续型随机变量随机变量的独立性二元随机变量的函数的分布所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。