例子

假设 概率王国 有三个县（A县、B县、C县），面积分布为 $P(A)、P(B)、P(C)$；这个国家的土地使用性质分为三类：住宅、工厂和农田，它们的面积分别为：$P(住宅)、P(工厂)、P(农田)$这些面积的和就是整个国家的面积：
$$\begin{array}{l}P(A)+P(B)+P(C)=1\\ P(住宅)+P(工厂)+P(农田)=1\end{array}$$

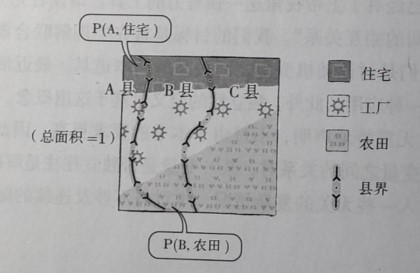
由以上所知，我们定义如下信息：

• $P(A)$：A 县的全体面积；$P(B)$：B 县的全体面积；$P(C)$：C 县的全体面积；
• $P(住宅)$：全国的住宅面积；$P(工厂)$：全国的工厂面积；$P(农田)$：全国的农田面积；
• $P(A，住宅)$：A 县的住宅面积；$P(A，工厂)$：A 的工厂面积；$P(A，农田)$：A 的农田面积；
• $P(B,住宅),P(B,工厂),P(B,农田);P(C,住宅),P(C,工厂),P(C,农田)$ 含义类似;

我们定义随机变量 $X$，它的取值范围为：$A,B,C$；定义随机变量 $Y$，它的取值范围为：$住宅、工厂、农田$；

联合概率和条件概率

我们定义形如 $P(X=a,Y=b)$，这类包含多个条件且所有条件同时成立的概率为 联合概率；
形如 $P(X=a)$ 或者 P(Y = b) 这类仅单个随机变量的概率为 边缘概率；
联合概率 与 边缘概率 具有如下关系：

$$\begin{array}{l}P(X=a)={\sum }_{b}P(X=a,Y=b)\\ P(Y=b)={\sum }_{a}P(X=a,Y=b)\end{array}$$

全国的住宅、工厂、农田面积可以如此得到：
$$\begin{array}{l}P(Y=住宅)=P(X=A,Y=住宅)+P(X=B,Y=住宅)+P(X=C,Y=住宅)\\ P(Y=工厂)=P(X=A,Y=工厂)+P(X=B,Y=工厂)+P(X=C,Y=工厂)\\ P(Y=农田)=P(X=A,Y=农田)+P(X=B,Y=农田)+P(X=C,Y=农田)\end{array}$$

A、B、C三县的面积可以如下得到：
$$\begin{array}{l}P(X=A)=P(X=A,Y=住宅)+P(X=A,Y=工厂)+P(X=A,Y=农田)\\ P(X=B)=P(X=B,Y=住宅)+P(X=B,Y=工厂)+P(X=B,Y=农田)\\ P(X=C)=P(X=C,Y=住宅)+P(X=C,Y=工厂)+P(X=C,Y=农田)\end{array}$$

全国的总面积可以如此得到：
$$\begin{array}{l}P(X=A,Y=住宅)+P(X=A,Y=工厂)+P(X=A,Y=农田)\\ +P(X=B,Y=住宅)+P(X=B,Y=工厂)+P(X=B,Y=农田)\\ +P(X=C,Y=住宅)+P(X=C,Y=工厂)+P(X=C,Y=农田)\\ =1\end{array}$$

条件概率

形如 $P(Y=b|X=a)$ 这种表达式的含义为：在事件 $X=a$ 发生的前提下，事件 $Y=b$ 的概率，我们称这样的概率为 条件概率；
条件概率的定义如下：
$$P(Y=b|X=a)=\frac{P(X=a，Y=b)}{P(X=a)}$$

条件概率具有如下形式：
$$穷尽Y的取值之后，有\sum _{b}P(Y=b|X=a)=1（这个1表示的是比例）;$$

例如，我们想知道 A 县中，住宅、工厂、农田所站的比重，可以有如下计算：
$$\begin{array}{l}P(Y=住宅|X=A)=\frac{P(X=A，Y=住宅)}{P(X=A)}\\ P(Y=工厂|X=A)=\frac{P(X=A，Y=工厂)}{P(X=A)}\\ P(Y=农田|X=A)=\frac{P(X=A，Y=农田)}{P(X=A)}\end{array}$$

贝叶斯公式：

假设我们得到以下信息：

• 各县的面积为：$P(A)=0.2$、$P(B)=0.32$、$P(C)=0.48$;
• A 县的详情为：$P(住宅|A)=0.2$；$P(工厂|A)=0.6$；$P(农田|A)=0.2$；
• B 县的详情为：$P(住宅|B)=0.5$；$P(工厂|B)=0.25$；$P(农田|B)=0.25$；
• C 县的详情为：$P(住宅|C)=0.25$；$P(工厂|C)=0.25$；$P(农田|C)=0.5$；
• 求此时 P(A|工厂)是多少？可以理解为：A县工厂的面积占全国工厂总面积的比例？

这个问题可以抽象为：我们由一组 $P(县)$ 与 $P(用途|县)$ 构成的关系式推导出 $P(县|用途)$?
我们的求解可以用 A县的工厂面积 除以 全国工厂总面积：
$$P(A|工厂)=\frac{P(A，工厂)}{P(工厂)}$$

其中，分子 $P(A,工厂)$ 可以由：
$$P(A，工厂)=P(工厂|A)P(A)$$
得到

分母 $P(工厂)$ 可以由：
$$\begin{array}{rl}P(工厂)& =P(A，工厂)+P(B,工厂)+P(C,工厂)\\ & =P(工厂|A)P(A)+P(工厂|B)P(B)+P(工厂|C)P(C)\end{array}$$

所以最终，表达式如下：
$$\begin{array}{rl}P(A|工厂)& =\frac{P(A，工厂)}{P(工厂)}\\ & =\frac{P(工厂|A)P(A)}{P(A，工厂)+P(B,工厂)+P(C,工厂)}\\ & =\frac{P(工厂|A)P(A)}{P(工厂|A)P(A)+P(工厂|B)P(B)+P(工厂|C)P(C)}\end{array}$$

由上述式子可以得到关于贝叶斯公式的概念：
已知 $P(X=[A,B,C])$ 和 P(Y = [住宅、工厂、农田] | X = [A, B, C])，要求 $P(X=A|Y=工厂)$ ? 其公式可以如下：
$$\begin{array}{rl}P(X=A|Y=工厂)& =\frac{P(X=A，Y=工厂)}{P(Y=工厂)}\\ & =\frac{P(Y=工厂|X=A)P(X=A)}{{\sum }_{X=[A，B，C]}P(X,Y=工厂)}\\ & =\frac{P(Y=工厂|X=A)P(X=A)}{{\sum }_{X=[A，B，C]}P(Y=工厂|X)P(X)}\end{array}$$

上述公式被称为 贝叶斯公式；

独立性

假设存在多个事件A 和 B，独立性是指：事件 A 发生与否与事件 B 发生与否毫无关联，此时可以称事件A 和 B 相互独立；
相互独立的事件 A 和 B 具有如下性质：

• 条件概率与条件无关：$P(X=a|Y=b)=P(X=a)$ 与 Y 无关；
• 联合概率是边缘概率的乘积：$P(X=a,Y=b)=P(X=a)P(Y=b)$;

最后

以上就是忧虑斑马最近收集整理的关于多随机变量之间的关系例子联合概率和条件概率条件概率贝叶斯公式：独立性的全部内容，更多相关多随机变量之间内容请搜索靠谱客的其他文章。