多元线性回归的spss应用

多元线性回归的spss应用

我们先从一元回归引入。
对于一元的回归，方法选择哪一个都没有太大影响。

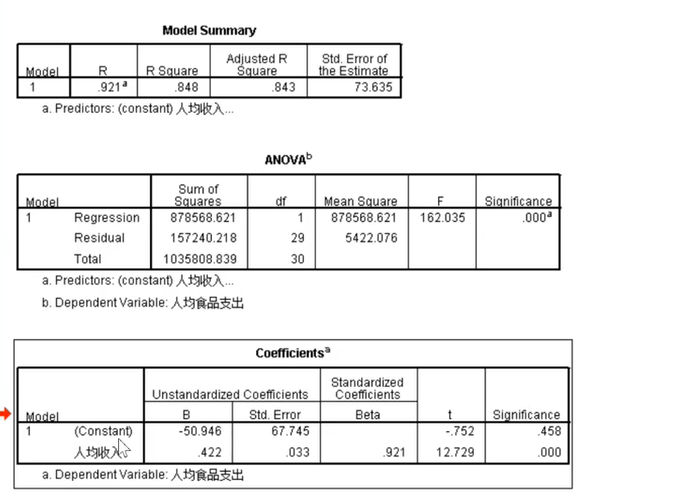
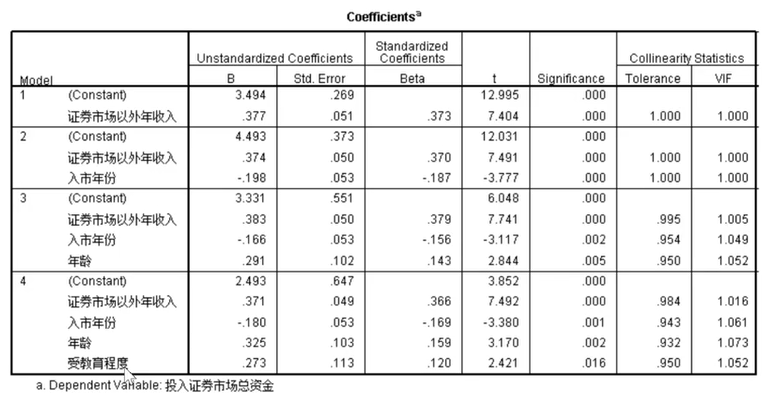
第一个表格描述的是方程解释现实情况的程度，为84.8%，第二个表格则是方差分析，可以从最后一列推断出通过方差分析，唯一的自变量前的系数不为零，第三个表用于判断取标准化系数还是非标准化系数，如果常数项的检验值小于0.05则取非标准化系数(B)，否则取标准化系数（BETA）。

接下来来到多元回归了，先选择方法中的进入。

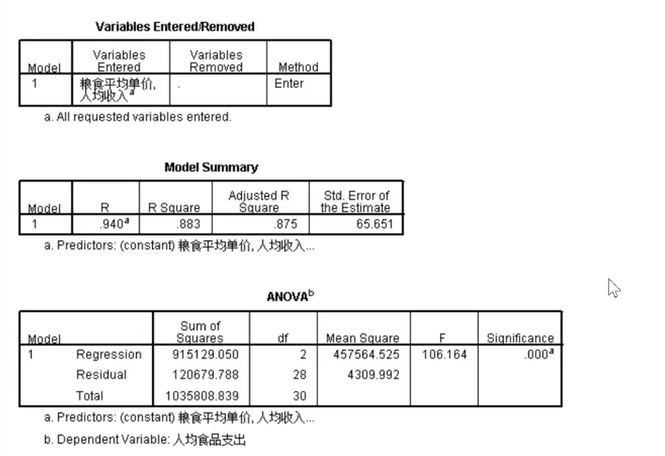
进入就是一开始让所有因素都进入方程，再在之后的检验中剔除，上图中第一个表只有一个模型，说明所有因素都通过偏检验了，所以没有变量被剔除了。
现在改成向前。

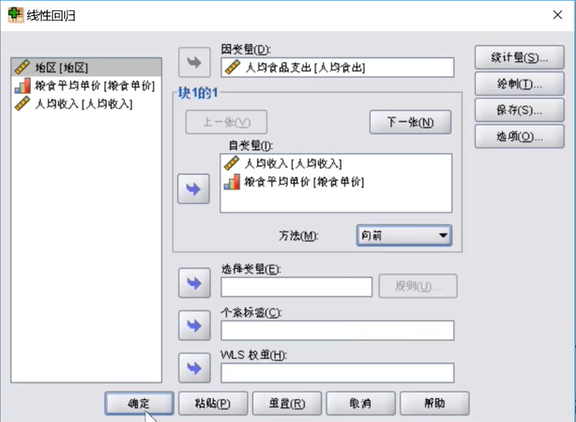
向前相当于一开始不加变量，逐步将变量加入到模型中。

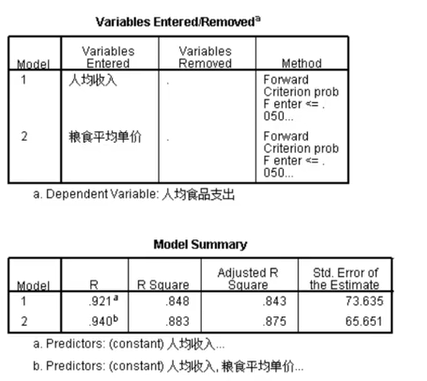
第一张表介绍了引入变量的步骤，第二张表介绍了两次引入变量生成的模型的解释功能，可以看到模型的判定系数从0.843提升到了0.875。
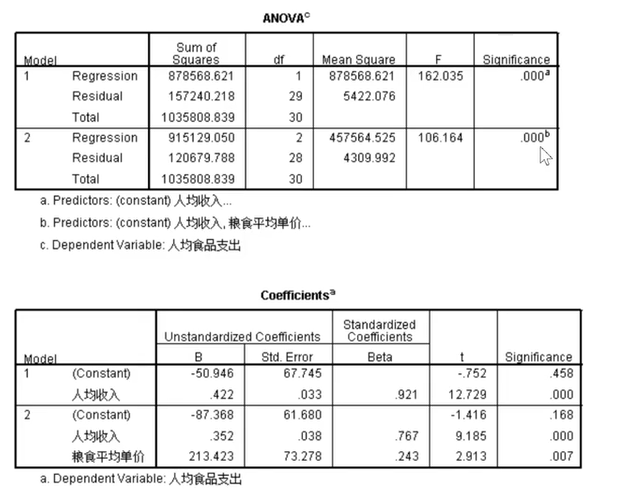第一张图直接看第二个式子，ANOVA分析用于验证这个问题适不适合用线性回归，只要通过了这个就可以继续，如果没有通过则之后的表都不用看了，这个问题得换一个模型了。
在这里显然是通过了检验，我们往下看第二张表，由于第二个模型比第一个模型好，所以我们直接读第二个模型，在这里常数项被拒绝了，所以我们读标准化后的系数。
再改成向向后。
默认一开始所有变量均进入模型，如果某个变量偏检验不通过就把它剔除。

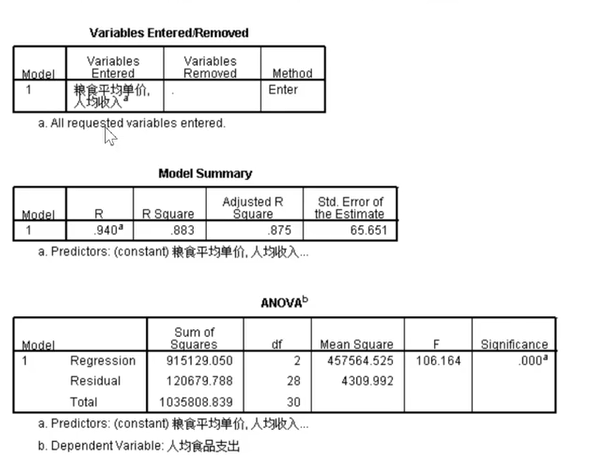
从表一可以看出，没有变量被剔除，因此表一只有一行。

紧接着改成逐步，它的意思就是一边进一边出，在实际的多元回归分析中，我们会更多地考虑这个方法。

我们可以看到，两次有变量进入，但都没有变量没有通过偏检验被移除。

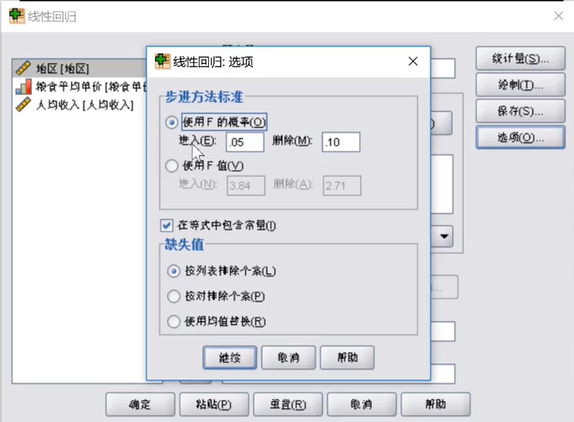
在这里我们可以找到所有方法默认的变量进入与删除的余值，显然f<=0.05时可以进入，f>=0.1时必须删除。

逐步分析的好处是迭代次数少，容易得到最终的结果。

接下来看多元逻辑斯蒂回归模型：（我们这里用的方法是向前）

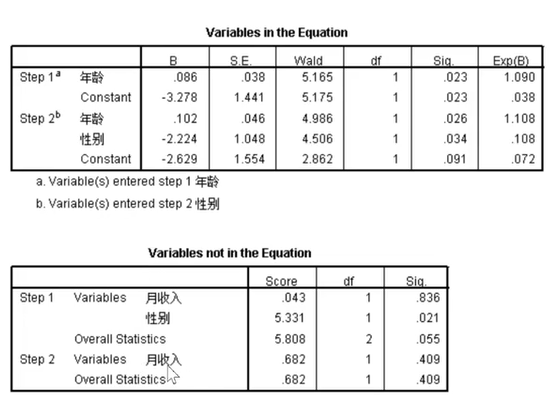
在这里，由于月收入的偏检验未通过，所以它始终没有被加入到方程中。

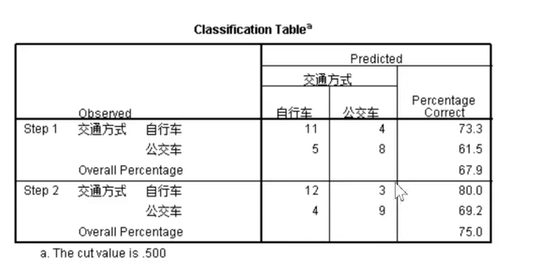
这是分类问题的混淆矩阵，用于检验用新模型进行预测，所得到的结果的准确性。以第一行为例，在实际用自行车的人中，有11个人被模型预测为用了自行车，有4个人被模型预测为用了公交车，因此预测的准确率为73.3%。
the cut value is 0.5指的是以0.5作为概率的切分。

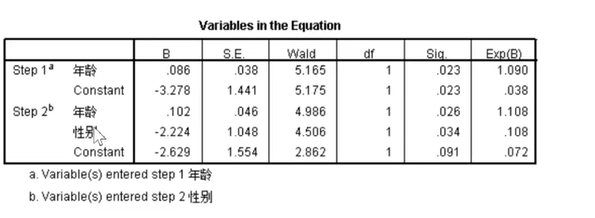
这个表格还有一点特别有意思，就是wald可以用来对加入的变量的影响程度进行排序，比如在最终模型中，年龄的影响大于性别。

最后是在操作中可能会遇到的三类基本问题。

我们可以在数据分析时选中共线性诊断，最后的结果会出现这么一张表，看有没有tolerance小于0.1的：

没有，继续找，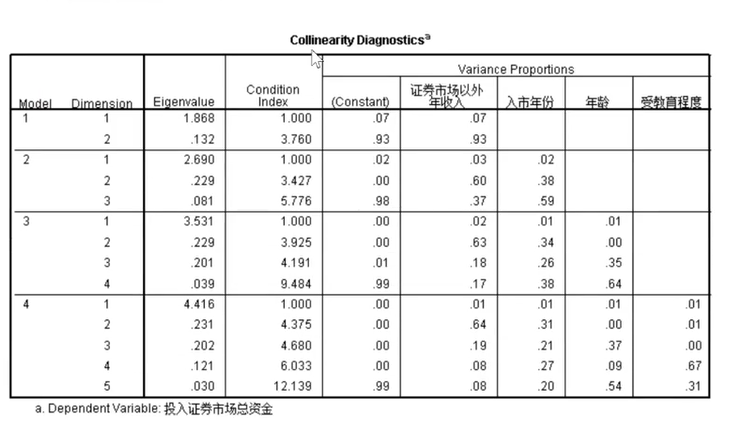
elgenvalue属于特征根，看有没有特征根等于0，也没有。
看Condition index，即条件指数，看有没有条件指数大于30的，貌似也没有。所以当前模型没有多重共线性。

最后

以上就是怕孤独花瓣为你收集整理的多元线性回归的spss应用的全部内容，希望文章能够帮你解决多元线性回归的spss应用所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。