多元线性回归matlab代码_多元线性回归分析终稿

一、背景

多元回归分析又称多对多回归是指在相关变量中将一个变量视为因变量，其他一个或多个变量视为自变量，建立多个变量之间线性或非线性数学模型数量关系式并利用样本数据进行分析的统计分析方法。在132位顾客中选择了第1位客户，以喜好程度作为因变量，以价格、可口可乐 or 百事可乐、有糖 or 无糖作为自变量，运用多元线性回归方法分析这位客户对不同轮廓的可乐喜爱度。通过分析得出，价格、可口可乐or百事可乐、有糖or无糖显著影响因变量喜爱度。

二、数据分析

1.线性拟合度高，回归直线能够描述喜爱度98%的变化

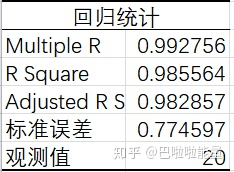
分析：R为0.992756，接近1

R^2为0.985564，也接近1

2.所有自变量在整体上看对于因变量喜爱度的线性显著性高，回归方程有效。

分析：significance F=6.2566E-15，小于0.05，所以所有自变量在整体上看对于因变量喜爱度的线性显著性高，回归方程有效。

3.喜爱度与价格负相关，当可乐为可口可乐时，喜爱度高，当有糖时，喜爱度高。三个自变量的回归系数具有显著性。

分析：

①回归系数分析

以喜爱度为因变量，价格、可乐种类、是否含糖为自变量，回归系数分别为-9.6 、8.4、 3.8，则价格上升一块钱，（其余两个变量不变动），喜爱度降低9.6；当可乐为可口可乐时（其余两个变量不变动），喜爱度高；当有糖时（其余两个变量不变动），喜爱度高。且对价格因素最敏感。

②t检验分析

P（价格）=1.31E-14，小于0.05，所以自变量价格对于因变量喜爱度的线性显著性高。

P（可口or百事）=4.82E-14，小于0.05，所以该自变量对于因变量喜爱度的线性显著性高。

P（有糖or无糖）=7.47E-09，小于0.05，所以该自变量对于因变量喜爱度的线性显著性高。

得出最终线性回归方程

Y=-9.6价格+8.4可口or百事+3.8有糖or无糖+46.6

三、总结

线性回归方程

Y=-9.6价格+8.4可口or百事+3.8有糖or无糖+46.6

该方程线性拟合度好，三个变量都显著影响喜爱度。且说明1号客户喜爱为低价格、可口可乐、有糖，且价格因素对喜爱度影响最大。

注：

可口可乐为1，百事可乐为0

有糖为1，无糖为0

T检验用于对某一自变量Xi对于Y的线性显著性，若某一Xi不显著，意味可以从模型中剔除这个变量，使得模型更简洁。

F检验用于对所有的自变量X在整体上看对于Y的线性显著性

T检验的结果看P-value，F检验看Significant F值