基于多元线性回归的房价预测

摘要

市场房价的走向受到多种因素的影响，通过对影响市场房价的多种因素进行分析，有助于对未来房价的走势进行较为准确的评估。
多元线性回归适用于对受到多因素影响的数据进行分析的场景。由多个自变量的最优组合共同来预测或估计因变量，比只用一个自变量进行预测或估计更有效，更符合实际。本文基于数学模型，对过去一段时间某一地区的房屋出售价格等相关数据进行整理，利用多元线性回归的方法对数据进行分析，预测该地区未来的房价走势。
关键词：多元线性回归；房价预测；数据分析；

引言

对未来房价进行预测，在一定程度上影响着社会经济的发展。广义上讲，精确的房价预测有助于国家对市场房价走势的宏观调控，小范围来讲，未来房价预测是企业战略规划的一部分，对于消费者而言，房价预测为个人经济的合理规划起到了积极作用。由于房屋售价与多因素有关，并且房屋价格与影响房价的一些因素存在线性关系，所以选取多元线性回归模型研究该问题较为合适。
本次课题研究通过对某段时间某地区的已售房价数据进行线性回归分析，探索影响房价高低的主要因素，并对这些影响因素的影响程度进行分析，利用分析得到的数据，对未来房价的趋势和走向进行预测。

线性回归理论基础

一元线性回归是分析只有一个自变量（自变量x和因变量y）线性相关关系的方法。一元线性回归分析的数学模型为：y = a+bx+ε。
使用偏差平方和分别对参数a和参数b求偏导，可以得到线性模型的未知参数a、b的最小二乘估计值，其中，偏差平方和定义为∑(yi-a-bXi)2，a和b的唯一解如图2-1所示。

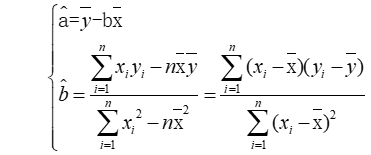
图2 1 参数的最小二乘估计
为了方便回归效果显著性检验，根据b的估计，引入LXX、LYY、LXY三个数学符号，这三个数学符号定义如图2-2所示。

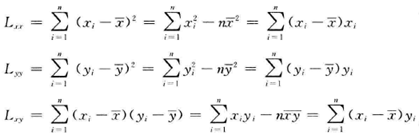
图 2 2 LXX、LYY、LXY的数学定义
在现实问题研究中，因变量的变化往往受几个重要因素的影响，此时就需要用两个或两个以上的影响因素作为自变量来解释因变量的变化，这就是多元回归。也就是说，当多个自变量与因变量之间是线性关系时，所进行的回归分析就是多元性回归。多元线性回归的数学模型为：y=β0+β1X1+β2X2+…++βpXp+ε。使用残差平方和分别对参数βi（i=0,1,…,p）求偏导，可以得到线性模型的未知参数βi（i=0,1,…,p）的估计值，β矩阵的估计值如图2-3所示。

回归效果的显著性检验

对平面上杂乱无章的点，利用最小二乘法求解出的线性回归方程是毫无意义的，线性回归反映出的趋势描述是否合理，需要一个数量指标来度量。
数据总的波动可以用离差平方和LYY来描述。它表示y的各次离差yi-y ̅的平方和。LYY数值越大，说明yi数值波动越大，也就是越分散。离差平方和LYY可以分解为回归直线上y的离差平方和U以及yi与回归直线上的y间的差的平方和Q。其中，U是由于x对y的线性相关关系引起的y的分散性，Q是由随机误差引起的分散性。yi-y ̅分解如图2-4所示。在总和中，U所占比重越大，说明随机误差所占的比重越小，回归效果越显著。故此，可以使用决定系数R2来度量线性回归效果是否显著，R2作为拟合优度，表示用直线来拟合数据的好坏，R2等于U/Lyy。

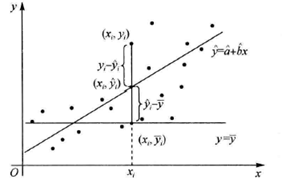
图2 4 yi-y ̅分解图
R2开方后的结果为皮尔逊相关系数，皮尔逊（Pearson）相关系数可以用来衡量两个数据集合是否在一条线上面，从而衡量定距变量间的线性关系。相关系数的绝对值越大，相关性越强；相关系数越接近于1或-1，相关度越强，相关系数越接近于0，相关度越弱。当|r|>=0.8时，x和y强相关，当|r|<0.3时，x和y弱相关。皮尔逊相关系数定义为如图2-5所示。

对于一元线性回归模型，线性回归模型效果的显著性可以通过假设检验问题H0：b=0；H1：b≠0进行判断，检验方法包括F检验法和t检验法。F检验属于回归方程显著性检验，是检验x与y是否相关的检验方法。t检验是回归系数显著性检验，是检验变量x是否有用的方法。H0成立时，两种检验方法定义如图2-6、图2-7所示。H0不成立时，对于给定的显著性水平α，当F>F1-α(1,n-2)时，回归效果显著。当|t|>t1-α/2(n-2)时，认为回归系数影响显著，否则回归系数的效果不显著。

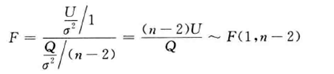
图2 6 一元线性回归F检验法

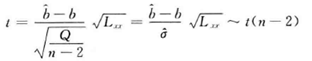
图2 7 一元线性回归t检验法
对于多元线性回归模型，回归效果的显著性可以使用F检验法通过假设检验问题H0：β0=β1=β2=…=βp=0；H1：βi（i=0,1,…,p）不全为0进行判断，H0成立时，F检验方法定义如图2-8所示。H0不成立时，对于给定的显著性水平α，当F>F1-α(p,n-p-1)时，回归效果显著。

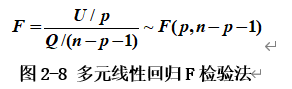
回归系数的显著性检验可以使用t检验法通过假设检验问题H0：βi=0；H1：βi≠0进行判断。H0成立时，t检验方法定义如图2-9所示。H0不成立时，对于给定的显著性水平α，当|t|>t1-α/2(n-p-1)时，认为回归系数影响显著，否则回归系数的效果不显著。

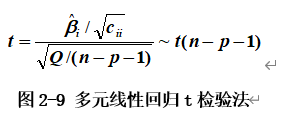
基于机器学习的线性回归与梯度下降

机器学习横跨计算机科学、工程技术和统计学等多个学科，渗透到了人们生产和生活中的各个领域，被广泛应用于各行各业之中，在当今世界激烈的竞争中，掌握和理解机器学习的基础模型和基本方法是非常有必要的。
机器学习中的线性回归模型以数理统计的线性回归模型为基础，它用一条直线对数据点进行拟合，在机器学习中，回归问题的求解过程就是寻找最佳拟合参数集的过程，也就是寻找满足使得估计值与实际值的方差最小时的参数解，这个过程用到了损失函数，损失函数定义如图2-10所示。利用损失函数，可以求解最佳拟合参数集。利用损失函数进行求解可以采用梯度下降法。

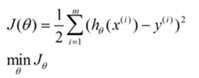
梯度下降法的计算过程就是沿梯度下降的方向求解极小值或沿梯度上升方向求解极大值。一般情况下，梯度向量为0的话说明是到了一个极值点，此时梯度的幅值也为0。采用梯度下降算法进行最优化求解时，算法迭代的终止条件是梯度向量的幅值接近0或接近一个非常小的常数阈值。梯度下降的过程如图2-11所示。

图2 11 梯度下降示意图

使用EXCEL进行数据分析

从总体数据中，选取29套房屋出售的部分数据如表3-1所示。


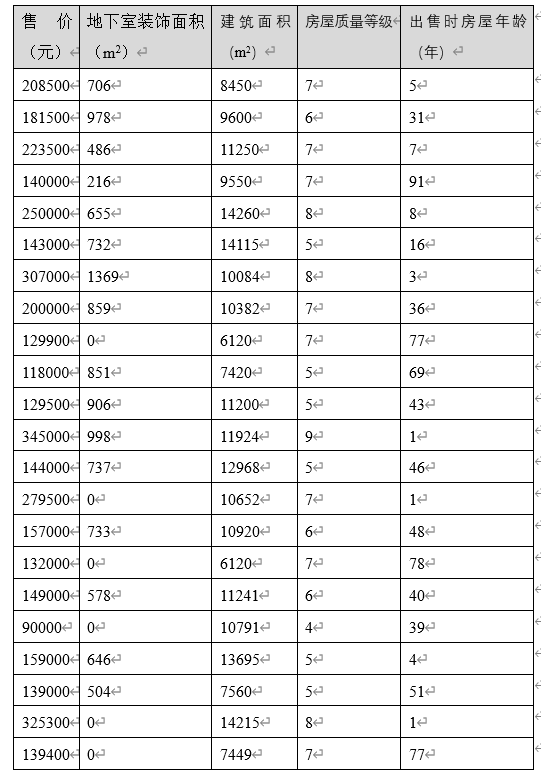
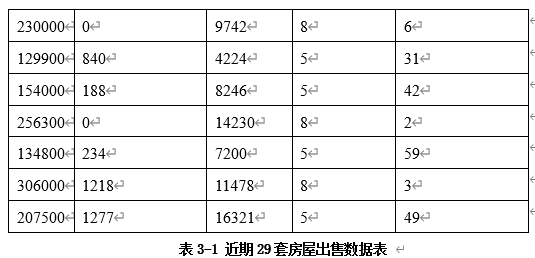
将房屋售价作为因变量，表格中的其他字段作为自变量，使用EXCEL对表3-1的数据进行部分回归分析，得到结果如图3-1所示。

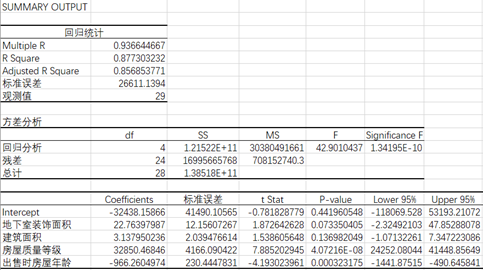
图3-1 回归分析结果
在图3-1中的回归统计子表中，字段Multiple R代表复相关系数R，也就是R2的平方根，又称相关系数，用来衡量自变量x与y之间的相关程度的大小。本次数据集回归分析得到的R=0.936644667，这表明x和y之间的关系为高度正相关。R Square是复测定系数，也就是相关系数R的平方。Adjusted R Square是调整后的复测定系数R2，该值为0.877303232，说明自变量能说明因变量y的87.73%，因变量y的12.27%要由其他因素来解释。标准误差用来衡量拟合程度的大小，也用于计算与回归相关的其它统计量，此值越小，说明拟合程度越好。观察值是用于估计回归方程的数据的观察值个数，本次数据集共有29条数据，所以观察值为29。
在图3-1中的方差分析子表中，Significance F为F检验显著性统计量，它的P值为1.34195E-10，小于显著性水平0.05，故而能够确定该回归方程回归效果显著，且方程中至少有一个回归系数显著不为0。
设因变量房屋售价为y，自变量地下室装饰面积为x1，自变量建筑面积为x2，自变量房屋质量等级为x3，自变量出售时房屋年龄为x4。在图3-1中的第三张子表中，Coefficients为常数项和b1～b4的值，据此便可以估算得出回归方程为：y= 22.76397987* x1+ 3.137950236* x2+ 32850.46846* x3+ (-966.2604974）* x4-32438.15866。但根据Coefficients估算出的回归方程可能存在较大的误差，在第三张子表中更为重要的一列是P-value列，P-value为回归系数t统计量的P值。由表中P-value的值可以发现，自变量房屋质量等级x3和出售时房屋年龄x4的P值远小于显著性水平0.05，因此这两个自变量与y相关。地下室装饰面积和建筑面积的P值大于显著性水平0.05，说这两个自变量与y相关性较弱，甚至不存在线性相关关系。

使用SPSS进行数据分析

在相关性未知的情况下，每次引入一个新的变量会对已有变量的重要程度造成影响，这时使用EXCEL分析显得有些复杂。房屋出售数据集共有16个自变量和1个因变量，共包含1460条记录。且相关性未知。数据集如图3-2所示。

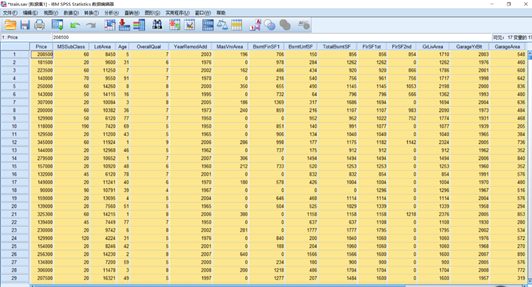
图3-2 1460套房屋出售的相关数据
导入数据后，使用前向逐步筛选法确定多元线性回归的相关系数。前向逐步筛选，是从一个自变量的选择开始，通过偏 F检验逐次引入一个最显著的变量。使用SPSS进行多元回归的参数设置如图3-3所示。

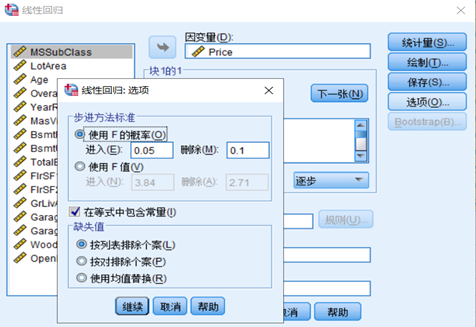
图3-3 参数设置
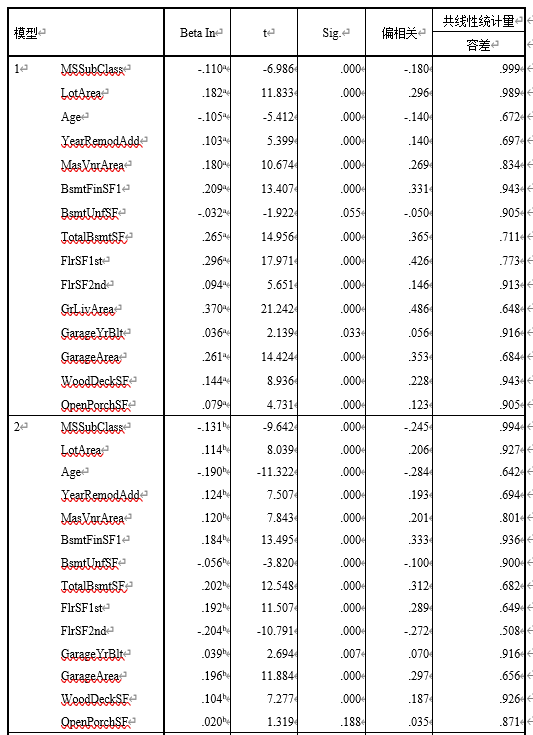
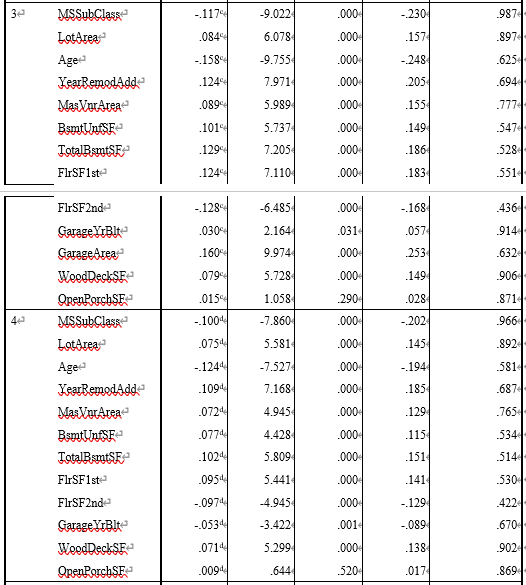
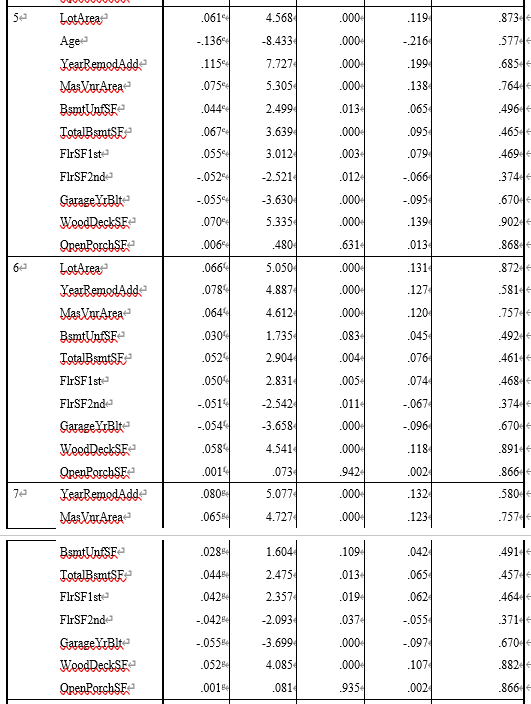
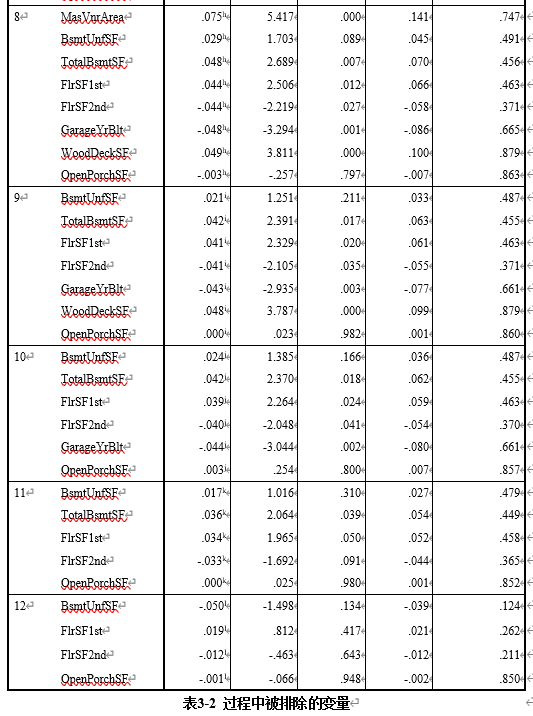
得到的回归模型因变量与自变量的相关性为81.9%。其中，被排除的变量如表3-2所示。最终模型中保留的变量包括：OverallQual,GrLivArea,BsmtFinSF1, GarageArea,MSSubClass,Age,LotArea,YearRemodAdd,MasVnrArea,WoodDeckSF,GarageYrBlt,TotalBsmtSF。对应的参数如图3-4所示。

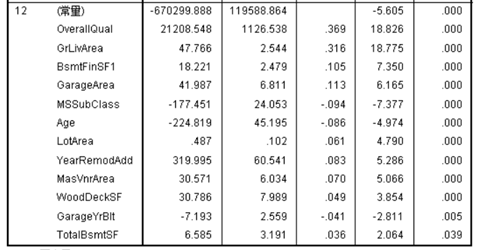
图3-4 最终的模型参数

房价预测

房价与房屋质量等级以及出售时房屋年龄两个影响因素存在线性相关关系，故使用这两个影响因素作为自变量x1和x2，建立线性回归模型。使用EXCEL对房屋售价和房屋质量等级以及出售时房屋年龄进行分析，得到数据分析结果如图4-1所示。

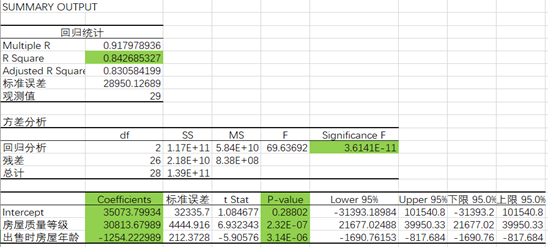
图4-1 重新选取变量后的回归分析结果
由图4-1可以确定建立线性回归模型：y= 35073.79934+ 30813.67989x1 -1254.222989x2。使用该模型即可实现对未来房价的预测。基于机器学习线性回归和梯度下降的方法，也可以确定回归方程。梯度法思想的三要素包括出发点、下降方向、下降步长。通过不断调整出发点和下降步长，可以使损失函数趋向于收敛，当损失函数收敛于一个接近于0的值的时候，此时得到的参数集就是原方程最合适的解。梯度下降源码如图4-2所示。

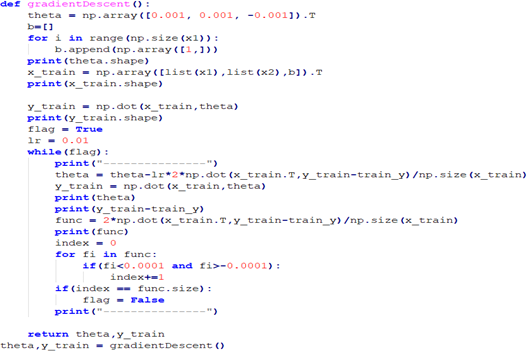
图4-2 梯度下降源码
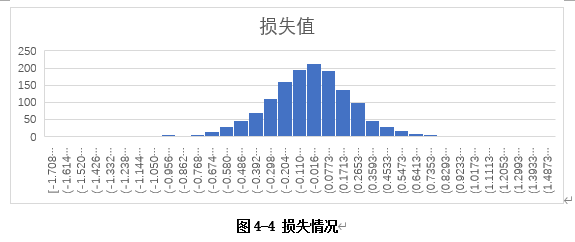
使用线性回归模型y= 35073.79934+ 30813.67989x1 -1254.222989x2对1430套房子的房价进行预测，该模型的预测结果较为准确。部分预测结果如图4-3所示。损失情况大致呈现正态分布，如图4-4所示。

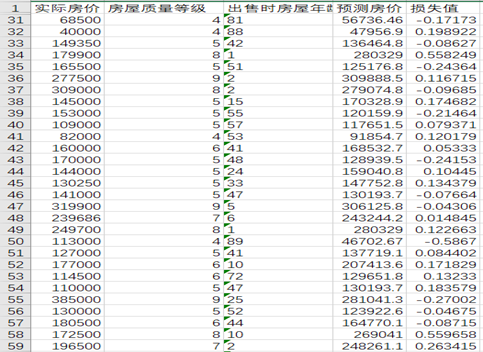
图4-3 房价预测结果

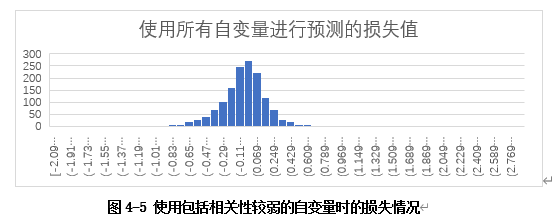
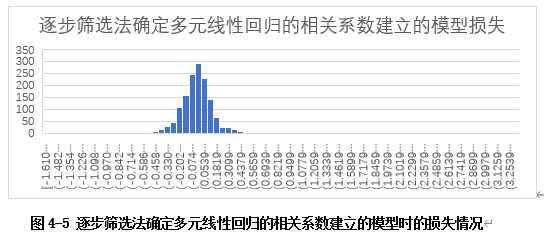
如果使用回归方程y= 22.76397987* x1+ 3.137950236* x2+ 32850.46846* x3+ (-966.2604974）* x4-32438.15866进行预测，损失比使用y= 35073.79934+ 30813.67989x1 -1254.222989x2模型要相对较大。使用回归方程y= 22.76397987* x1+ 3.137950236* x2+ 32850.46846* x3+ (-966.2604974）* x4-32438.15866进行预测的损失值分布如图4-5所示。

使用通过前向逐步筛选法确定多元线性回归的相关系数建立的模型进行预测，得到的损失曲线如图4-6所示。较之前的预测，使用该模型的损失情况最小。

总结

日常生活中，很多事物之间都是存在关联关系的，在这些关联关系中，线性关系是极为常见的。利用线性回归能够解决生活中遇到的与统计学有关的大多数问题，线性回归模型在统计学中占有重要地位。
使用数学方法对影响因变量的各种因素进行分析，可以快速确定自变量与因变量之间是否存在线性关系，能够帮助我们建立合适的数学模型。本次课题研究通过数学模型对房屋售价进行分析，通过前向逐步筛选法确定多元线性回归的相关系数并建立模型，通过建立的线性回归模型，在众多的自变量中找到了与房屋售价具有线性相关性的自变量，然后在此基础上建立多元线性回归模型，并使用该模型对房屋售价进行预测，得到了与真实值较为接近的估计值。

参考文献

[1] 孙海燕,周梦,李卫国,冯伟.数理统计.北京:北京航空航天大学出版社,2016.10

最后

以上就是暴躁冬瓜为你收集整理的基于多元线性回归的房价预测基于多元线性回归的房价预测的全部内容，希望文章能够帮你解决基于多元线性回归的房价预测基于多元线性回归的房价预测所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。