R方

结论

R方就是拟合回归最后对拟合回归效果的一个评价指标。R方 越接近于1，则拟合回归效果越好。

线性回归与最小二乘法

R方 - 相关系数p(y,y_head)

定义

R方是衡量模型拟合度的一个量,是一个比例形式，被解释方差/总方差。

公式：

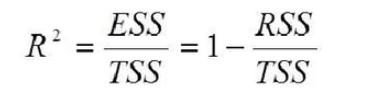
其中：TSS是执行回归分析前，响应变量固有的方差。

      RSS残差平方和就是，回归模型不能解释的方差。

      SSR回归模型可以解释的方差。

综上，R-squared 比列值区间在【0，1】

相关系数p(x,y)

推广 - 二次方程的相关系数

Reference：
https://www.zhihu.com/question/32021302

Adjustice R方

使用调整R方的原因

因为R-squared = SSR/TSS = 1 - RSS/TSS
因此，如果模型中增加一个自变量，即使这个自变量在统计上并不显著，R方也会变大。因此，为避免增加自变量而高估R方，统计学家提出用样本量（n）和自变量的个数（k）去调整R方，计算出调整的多重判定系数（调整的R方）
因此，需要adjusted R-squared ,它会对那些增加的且不会改善模型效果的变量增加一个惩罚向。
结论，如果单变量线性回归，则使用 R-squared评估，多变量，则使用adjusted R-squared。
在单变量线性回归中，R-squared和adjusted R-squared是一致的。
另外，如果增加更多无意义的变量，则R-squared 和adjusted R-squared之间的差距会越来越大，Adjusted R-squared会下降。但是如果加入的特征值是显著的，则adjusted R-squared也会上升
所以需要adjusted R-squared，它会对那些增加的且不会改善模型效果的变量增加一个惩罚项。

• N is the number of points in your data sample.（样本数量）
• K is the number of independent regressors, i.e. the number of variables in your model, excluding the constant.(即模型中变量的个数，不包括常数)

Multiple R

Multiple R：x和y的相关系数r，一般在-1~1之间，绝对值越靠近1则相关性越强，越靠近0则相关性越弱;
Multiple R 是线性回归的系数
R Square 是拟合系数
Adjusted R Square 调整后的拟合系数
Multiple r 不是线性回归系数，准确的说 他叫做 相关系数，但是可以通过它来判断 线性拟合程度。回归系数应该是β1

最后

以上就是眯眯眼花瓣为你收集整理的相关系数-回归分析-数据分析面试必备R方Adjustice R方Multiple R的全部内容，希望文章能够帮你解决相关系数-回归分析-数据分析面试必备R方Adjustice R方Multiple R所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。