[Machine Learning] 搭建神经网络（一层、二层和多层）

69 阅读 0 评论 46 点赞

我是靠谱客的博主开朗橘子，最近开发中收集的这篇文章主要介绍[Machine Learning] 搭建神经网络（一层、二层和多层），觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

1. 一层神经网络

2. 自己实现的二层神经网络

3. 基于TensorFlow的二层神经网络

4. 多层神经网络

5. 在多层神经网络中加入反向传播

1. 一层神经网络

搭建了一个最基本的一层神经网络，需要预先定义好权重和偏置，使用sigmod()函数作为激活函数。

import numpy as np

# 激活函数的定义
# 非线性转化方程(non-linear transformation function)， sigmoid函数(S 曲线)用来作为activation function
def sigmoid(x):
    # Our activation function: f(x) = 1 / (1 + e^(-x))
    return 1 / (1 + np.exp(-x))

class Neuron:
    def __init__(self, weights, bias):
        self.weights = weights
        self.bias = bias

    # 正向传播
    def feedforward(self, inputs):
        # Weight inputs, add bias, then use the activation function
        total = np.dot(self.weights, inputs) + self.bias
        return sigmoid(total)

weights = np.array([0, 1]) # w1 = 0, w2 = 1
bias = 1 # b = 4
n = Neuron(weights, bias)
x = np.array([2, 3]) # x1 = 2, x2 = 3
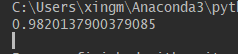
print(n.feedforward(x))

正向传播的输出

2. 自己实现的二层神经网络

采用面向对象编程方式，需要自己实现训练函数fit

神经网络模块

# 模块名：NeuralNetwork.py

import numpy as np

# 双曲函数
def tanh(x):
    return np.tanh(x)

# 双曲函数的导数,在更新权重的时候需要用到
def tanh_deriv(x):
    return 1.0 - np.tanh(x) * np.tanh(x)

# 逻辑函数（常用于0-1标准化）
def logistic(x):
    return 1 / (1 + np.exp(-x))

# 逻辑函数的导数
def logistic_derivative(x):
    return logistic(x) * (1 - logistic(x))

# 面向对象编程
class NeuralNetwork:
    # 构造函数
    # layers：每层有几个神经元(一个list)
    # 使用的标准化函数
    def __init__(self, layers, activation='tanh'):
        """
        :param layers: A list containing the number of units in each layer.
        Should be at least two values
        :param activation: The activation function to be used. Can be
        "logistic" or "tanh"
        """
        if activation == 'logistic':
            self.activation = logistic
            self.activation_deriv = logistic_derivative
        elif activation == 'tanh':
            self.activation = tanh
            self.activation_deriv = tanh_deriv

        # 空list,用于存放权重
        self.weights = []
        # 从第一从到最后一个隐藏层
        for i in range(1, len(layers) - 1):
            self.weights.append((2 * np.random.random((layers[i - 1] + 1, layers[i] + 1)) - 1) * 0.25) #生成i-1层到i层之间的权重
            self.weights.append((2 * np.random.random((layers[i] + 1, layers[i + 1])) - 1) * 0.25) #生成i层到i+1层之间的权重

    # 训练
    # X:训练集
    # class label 标记
    # Learning rate: 学习率
    # epochs: 更新权重和偏置的时候,采用抽样的方式进行更新
    def fit(self, X, y, learning_rate=0.2, epochs=10000):
        X = np.atleast_2d(X) #至少是二维的矩阵
        temp = np.ones([X.shape[0], X.shape[1] + 1]) #初始化原始矩阵
        temp[:, 0:-1] = X  # adding the bias unit to the input layer 将偏置向量添加到输入层
        X = temp
        y = np.array(y)  #转换成array

        for k in range(epochs):
            i = np.random.randint(X.shape[0])
            a = [X[i]]

            # 正向更新
            for l in range(len(self.weights)):  # going forward network, for each layer
                # Computer the node value for each layer (O_i) using activation function
                a.append(self.activation(np.dot(a[l], self.weights[l])))
            # 计算顶层的误差
            error = y[i] - a[-1]  # Computer the error at the top layer
            # For output layer, Err calculation (delta is updated error)
            deltas = [ error * self.activation_deriv(a[-1])]

            # 反向更新BP
            # Staring backprobagation
            for l in range(len(a) - 2, 0, -1):  # we need to begin at the second to last layer
                # Compute the updated error (i,e, deltas) for each node going from top layer to input layer
                deltas.append(deltas[-1].dot(self.weights[l].T) * self.activation_deriv(a[l]))
            deltas.reverse() # 因为是反向,所以需要颠倒
            for i in range(len(self.weights)):
                layer = np.atleast_2d(a[i])
                delta = np.atleast_2d(deltas[i])
                self.weights[i] += learning_rate * layer.T.dot(delta)

    def predict(self, x):
        x = np.array(x)
        temp = np.ones(x.shape[0] + 1)
        temp[0:-1] = x
        a = temp
        for l in range(0, len(self.weights)):
            a = self.activation(np.dot(a, self.weights[l]))
        return a

测试模块

import NeuralNetwork
import numpy as np

nn = NeuralNetwork.NeuralNetwork([2, 2, 1], 'tanh')
X = np.array([[0, 0], [0, 1], [1, 0], [1, 1]])
y = np.array([0, 1, 1, 0])
nn.fit(X, y) #训练神经网络模型
for i in [[0, 0], [0, 1], [1, 0], [1, 1]]:
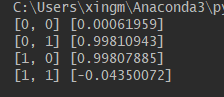
    print(i, nn.predict(i))

测试结果

3. 基于TensorFlow的二层神经网络

搭建一个基于TensorFlow的二层神经网络，输入层、隐藏层和输出层的节点个数分别为1、10和1。训练数据个数300，训练次数1000，激活函数选用ReLU。因为引入了TensorFlow，训练的过程可以不必自己实现。

import tensorflow as tf
import numpy as np

# 创建一个神经网络层
def add_layer(input, in_size, out_size, activation_function = None):
    """
    :param input:
        神经网络层的输入
    :param in_zize:
        输入数据的大小
    :param out_size:
        输出数据的大小
    :param activation_function:
        神经网络激活函数，默认没有
    """

    # 定义神经网络的初始化权重
    Weights = tf.Variable(tf.random_normal([in_size, out_size]))
    # 定义神经网络的偏置
    biases = tf.Variable(tf.zeros([1, out_size]) + 0.1)
    # 计算w*x+b
    W_mul_x_plus_b = tf.matmul(input, Weights) + biases
    # 根据是否有激活函数进行处理
    if activation_function is None:
        output = W_mul_x_plus_b
    else:
        output = activation_function(W_mul_x_plus_b)

    return output

# 创建一个具有输入层、隐藏层、输出层的三层神经网络，神经元个数分别为1,10,1
# 创建只有一个特征的输入数据，数据数目为300，输入层
x_data = np.linspace(-1, 1, 300)[:, np.newaxis]
# 创建数据中的噪声
noise = np.random.normal(0, 0.05, x_data.shape)
# 创建输入数据对应的输出
y_data = np.square(x_data) + 1 + noise

# 定义输入数据，None是样本数目，表示多少输入数据都行，1是输入数据的特征数目
xs = tf.placeholder(tf.float32, [None, 1])
# 定义输出数据，与xs同理
ys = tf.placeholder(tf.float32, [None, 1])

# 定义一个隐藏层
hidden_layer = add_layer(xs, 1, 10, activation_function = tf.nn.relu)

# 定义输出层
prediction = add_layer(hidden_layer, 10, 1, activation_function = None)

# 求解神经网络参数
# 定义损失函数
loss = tf.reduce_mean(tf.reduce_sum(tf.square(ys - prediction), reduction_indices = [1]))
# 定义训练过程
train_step = tf.train.GradientDescentOptimizer(0.1).minimize(loss)
# 变量初始化
init = tf.global_variables_initializer()
# 定义Session
sess = tf.Session()
# 执行初始化工作
sess.run(init)
# 进行训练
for i in range(1000):
    # 执行训练，并传入数据
    sess.run(train_step, feed_dict = {xs: x_data, ys: y_data})
    if i % 100 == 0:
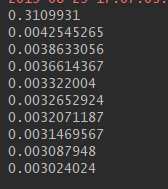
        print(sess.run(loss, feed_dict = {xs: x_data, ys: y_data}))
# 关闭Session
sess.close()

每训练100次打印一次loss的值，可以看出，随着训练次数的增多，loss越来越小，优化的余地也越来越少

参考：https://blog.csdn.net/Quincuntial/article/details/70148801

4. 多层神经网络

构建一个四层的神经网络（三层隐含层），思路基本一致，将初始话权值，计算损失值，调制权值的过程重复的多做几次就好了（也可以用循环）。

import numpy as np

class NeuralNetwork():
    def __init__(self, input):
        # random控制1以内的随机数作为初始权重
        np.random.seed(50)

        # 输入层3个神经元作为第一层
        # 第二层定义4个神经元
        layer2 = 4
        # 第三层定义5个神经元
        layer3 = 5
        # 第三层定义5个神经元
        layer4 = 4

        # 随机初始化各层权重
        self.synaptic_weights1 = 2 * np.random.random((input, layer2)) - 1
        self.synaptic_weights2 = 2 * np.random.random((layer2, layer3)) - 1
        self.synaptic_weights3 = 2 * np.random.random((layer3, layer4)) - 1
        self.synaptic_weights4 = 2 * np.random.random((layer4, 1)) - 1


    def __sigmoid(self, x):
        return 1 / (1 + np.exp(-x))

    def __sigmoid_derivative(self, x):
        return x * (1 - x)

    def train(self, training_set_inputs, training_set_outputs, number_of_training_iterations):
        for iteration in range(number_of_training_iterations):
            # 正向传播过程，即神经网络“思考”的过程
            activation_values2 = self.__sigmoid(np.dot(training_set_inputs, self.synaptic_weights1))
            activation_values3 = self.__sigmoid(np.dot(activation_values2, self.synaptic_weights2))
            activation_values4 = self.__sigmoid(np.dot(activation_values3, self.synaptic_weights3))
            output = self.__sigmoid(np.dot(activation_values4, self.synaptic_weights4))

            # 计算各层损失值
            delta5 = (training_set_outputs - output) * self.__sigmoid_derivative(output)
            delta4 = np.dot(self.synaptic_weights4, delta5.T) * (self.__sigmoid_derivative(activation_values4).T)
            delta3 = np.dot(self.synaptic_weights3, delta4.T) * (self.__sigmoid_derivative(activation_values3).T)
            delta2 = np.dot(self.synaptic_weights2, delta3) * (self.__sigmoid_derivative(activation_values2).T)

            # 计算需要调制的值
            adjustment4 = np.dot(activation_values4.T, delta5)
            adjustment3 = np.dot(activation_values3.T, delta4)
            adjustment2 = np.dot(activation_values2.T, delta3.T)
            adjustment1 = np.dot(training_set_inputs.T, delta2.T)

            # 调制权值
            self.synaptic_weights1 += adjustment1
            self.synaptic_weights2 += adjustment2
            self.synaptic_weights3 += adjustment3
            self.synaptic_weights4 += adjustment4

    def think(self, inputs):
        activation_values2 = self.__sigmoid(np.dot(inputs, self.synaptic_weights1))
        activation_values3 = self.__sigmoid(np.dot(activation_values2, self.synaptic_weights2))
        activation_values4 = self.__sigmoid(np.dot(activation_values3, self.synaptic_weights3))
        output = self.__sigmoid(np.dot(activation_values4, self.synaptic_weights4))
        return output

if __name__ == "__main__":
    neural_network = NeuralNetwork(3) #三个输入，分别是像素的b、g、r分量
    print("Random starting synaptic weights (layer 1): ")
    print(neural_network.synaptic_weights1)
    print("nRandom starting synaptic weights (layer 2): ")
    print(neural_network.synaptic_weights2)
    print("nRandom starting synaptic weights (layer 3): ")
    print(neural_network.synaptic_weights3)
    print("nRandom starting synaptic weights (layer 4): ")
    print(neural_network.synaptic_weights4)

    # 训练集不变
    training_set_inputs = np.array([[0, 0, 1], [1, 1, 1], [1, 0, 1], [0, 1, 1]])
    training_set_outputs = np.array([[0, 1, 1, 0]]).T
    # training_set_inputs = np.array([[123/255, 123/255, 54/255], [255/255, 12/255, 205/255], [1/255, 234/255, 255/255], [0/255, 1/255, 1/255]])
    # training_set_outputs = np.array([[110/255, 165/255, 210/255, 13/255]]).T

    neural_network.train(training_set_inputs, training_set_outputs, 10000)
    print("nNew synaptic weights (layer 1) after training: ")
    print(neural_network.synaptic_weights1)
    print("nNew synaptic weights (layer 2) after training: ")
    print(neural_network.synaptic_weights2)
    print("nNew synaptic weights (layer 3) after training: ")
    print(neural_network.synaptic_weights3)
    print("nNew synaptic weights (layer 4) after training: ")
    print(neural_network.synaptic_weights4)

    # 新样本测试
    # print("nConsidering new situation [255/255, 12/255, 205/255] -> 95?: ")
    # print(255 * neural_network.think(np.array([255/255, 12/255, 205/255])))
    print("nConsidering new situation [1, 0, 0] -> ?: ")
    print(neural_network.think(np.array([0, 1, 1])))
    print("Considering new situation [1, 1, 1] -> ?: ")
    print(neural_network.think(np.array([1, 1, 1])))
    print("Considering new situation [0, 0, 1] -> ?: ")
    print(neural_network.think(np.array([0, 0, 1])))

5. 在多层神经网络中加入反向传播

优化方法 : 梯度下降法
Layers : n fully-connected layers
损失函数 : 平方和误差

import numpy as np
np.seterr(over='ignore')

class NeuralNetwork():
    def __init__(self):
        np.random.seed(1)  # Seed the random number generator
        self.weights = {}  # Create dict to hold weights
        self.num_layers = 1  # Set initial number of layer to one (input layer)
        self.adjustments = {}  # Create dict to hold adjustements

    def add_layer(self, shape):
        # Create weights with shape specified + biases
        self.weights[self.num_layers] = np.vstack((2 * np.random.random(shape) - 1, 2 * np.random.random((1, shape[1])) - 1))
        # Initialize the adjustements for these weights to zero
        self.adjustments[self.num_layers] = np.zeros(shape)
        self.num_layers += 1

    def __sigmoid(self, x):
        return 1 / (1 + np.exp(-x))

    def __sigmoid_derivative(self, x):
        return x * (1 - x)

    def predict(self, data):
        # Pass data through pretrained network
        for layer in range(1, self.num_layers+1):
            data = np.dot(data, self.weights[layer-1][:, :-1]) + self.weights[layer-1][:, -1] # + self.biases[layer]
            data = self.__sigmoid(data)
        return data

    def __forward_propagate(self, data):
        # Progapagate through network and hold values for use in back-propagation
        activation_values = {}
        activation_values[1] = data
        for layer in range(2, self.num_layers+1):
            data = np.dot(data.T, self.weights[layer-1][:-1, :]) + self.weights[layer-1][-1, :].T # + self.biases[layer]
            data = self.__sigmoid(data).T
            activation_values[layer] = data
        return activation_values

    def simple_error(self, outputs, targets):
        return targets - outputs

    def sum_squared_error(self, outputs, targets):
        return 0.5 * np.mean(np.sum(np.power(outputs - targets, 2), axis=1))

    def __back_propagate(self, output, target):
        deltas = {}
        # Delta of output Layer
        deltas[self.num_layers] = output[self.num_layers] - target

        # Delta of hidden Layers
        for layer in reversed(range(2, self.num_layers)):  # All layers except input/output
            a_val = output[layer]
            weights = self.weights[layer][:-1, :]
            prev_deltas = deltas[layer+1]
            deltas[layer] = np.multiply(np.dot(weights, prev_deltas), self.__sigmoid_derivative(a_val))

        # Caclculate total adjustements based on deltas
        for layer in range(1, self.num_layers):
            self.adjustments[layer] += np.dot(deltas[layer+1], output[layer].T).T

    def __gradient_descente(self, batch_size, learning_rate):
        # Calculate partial derivative and take a step in that direction
        for layer in range(1, self.num_layers):
            partial_d = (1/batch_size) * self.adjustments[layer]
            self.weights[layer][:-1, :] += learning_rate * -partial_d
            self.weights[layer][-1, :] += learning_rate*1e-3 * -partial_d[-1, :]


    def train(self, inputs, targets, num_epochs, learning_rate=1, stop_accuracy=1e-5):
        error = []
        for iteration in range(num_epochs):
            for i in range(len(inputs)):
                x = inputs[i]
                y = targets[i]
                # Pass the training set through our neural network
                output = self.__forward_propagate(x)

                # Calculate the error
                loss = self.sum_squared_error(output[self.num_layers], y)
                error.append(loss)

                # Calculate Adjustements
                self.__back_propagate(output, y)

            self.__gradient_descente(i, learning_rate)

            # Check if accuarcy criterion is satisfied
            if np.mean(error[-(i+1):]) < stop_accuracy and iteration > 0:
                break

        return(np.asarray(error), iteration+1)


if __name__ == "__main__":

    # ----------- XOR Function -----------------

    # Create instance of a neural network
    nn = NeuralNetwork()

    # Add Layers (Input layer is created by default)
    nn.add_layer((2, 9))
    nn.add_layer((9, 1))

    # XOR function
    training_data = np.asarray([[0, 0], [0, 1], [1, 0], [1, 1]]).reshape(4, 2, 1)
    training_labels = np.asarray([[0], [1], [1], [0]])

    error, iteration = nn.train(training_data, training_labels, 5000)
    print('Error = ', np.mean(error[-4:]))
    print('Epoches needed to train = ', iteration)

    # nn.predict(testing_data)