第四章 平稳序列的拟合与预测

4.1 建模步骤

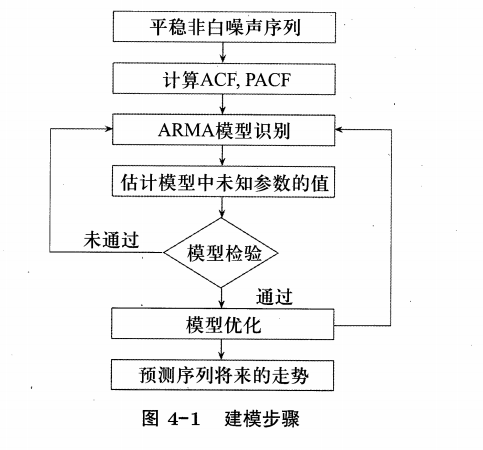
当我们拿到一组数据，想要通过这组数据来探究过去发生的规律，研究现在发生的强度并预测未来事情的发展走向，就需要从这些数据中挖掘出事物发生的特征，比如频率、强度、集中值等等，来提取“经验”，对过去的作出反应，弥补或者提取收益，而后建立一个合适的模型，来预测未来事物的发展，掌握未来动态，并及时调整，做好准备。

对于时间序列数据，当我们拿到数据时，我们首先要对数据进行预处理，事实上，所有的数据都是如此，经过预处理使之成为合适的，可以进行预测的，有用的数据。

时间序列数据的预处理是要进行平稳性检验，只有平稳的时间序列数据才是可以利用的，有效的数据，才能进行预测。还要进行纯随机检验，确保其是非白噪声序列。

4.2 模型识别

若数据是平稳的非白噪声序列，则可以考虑建模，但时间序列模型不止一种，具体要用哪种模型要根据数据的特征来判断，即先计算样本的ACF和PACF。根据样本的自相关系数和偏自相关系数的截尾和拖尾性来选择合适的模型拟合观察值序列。

定阶的基本原则如下：

但是由于样本的随机性，样本的相关系数不会呈现出理论上的截尾的完美情况，应该截尾的样本自相关系数或偏自相关系数就会呈现出小值震荡。同时，又因为平稳时间序列通常具有的短期相关性，随着延迟阶数趋近于无穷，$\widehat{{\rho }_k}$与$\widehat{{\varphi }_{kk}}$都会衰减至零值附近作小值波动。

这就给我们留下了一个问题，判断拖尾的标准情况是什么？其实并没有，主要还是依靠分析人员的主观经验。根据诸多统计学家的证明，样本自相关系数是总体自相关系数的有偏估计，当k足够大时，根据平稳序列自相关系数呈负指数衰减，有${\rho }_k\to 0$，而当样本容量n充分大时，样本的自相关系数和偏自相关系数都是近似于正态分布，根据正态分布的性质，可以利用2倍标准差范围辅助判断。

如果样本自相关系数或偏自相关系数在最初的d阶明显超过2倍标准差范围，而后几乎95%的自相关系数都落在2倍标准差的范围以内，而且由非零自相关系数衰减为小值波动的过程非常突然，这时，通常视为自相关系数截尾。截尾阶数为d。

如果有超过5%的样本自相关系数落入2倍标准差范围之外，或者由显著非零的自相关系数衰减为小值波动的过程非常连续或比较缓慢，这时，通常视为自相关系数不截尾。

4.3 参数估计

对于非中心化的ARMA(p,q)模型，有$x_t=\mu +\frac{{\Theta }_q(B)}{{\Phi }_q(B)}{ϵ}_t$，式中${ϵ}_t\sim WN(0,{\sigma }_{ϵ}^2)$【WN白噪声】。模型中共含有p+q+2个未知参数：${\theta }_1,{\theta }_2,\cdots ,{\theta }_q,{\varphi }_1,{\varphi }_2,\cdots ,{\varphi }_p,\mu ,{\sigma }_{ϵ}^2$。

参数$\mu$是序列均值，通常采用一阶中心距的估计方法，用样本均值估计总体均值即可得到它的估计值。

再将原序列中心化，则待估参数减少至p+q+1个。对这些参数有三种估计方法：距估计、极大似然估计、最小二乘估计。

4.3.1 距估计

用p+q个样本自相关系数估计总体自相关系数，构造p+q个方程组成的Yule-Walker方程组
$$\{\begin{array}{l}{\rho }_1({\varphi }_1,\cdots ,{\varphi }_p,{\theta }_1,\cdots ,{\theta }_q)=\widehat{{\rho }_1}\\ ⋮\\ {\rho }_{p+q}({\varphi }_1,\cdots ,{\varphi }_p,{\theta }_1,\cdots ,{\theta }_q)=\widehat{{\rho }_{p+q}}\end{array}$$
从中解出的参数值$\widehat{{\varphi }_1},\cdots ,\widehat{{\varphi }_p},\widehat{{\theta }_1},\cdots ,\widehat{{\theta }_q}$就是${\varphi }_1,\cdots ,{\varphi }_p,{\theta }_1,\cdots ,{\theta }_q$的距估计。

尤尔—沃克方程（Yule-Walker equation）是描述自回归序列参数与其协方差函数之间关系的方程。

所以，距估计其实就是建立多个自相关系数与参数的方程，而后解出参数（因为$\rho$可估或者说是已知）。

4.3.2 极大似然估计

在极大似然准则下（事件既然发生，则其概率就一定尽可能大），认为样本来自使该样本出现大概率最大的总体。因此未知参数的极大似然估计就是使得似然函数（即联合密度函数）达到最大的参数值。
L ( β 1 ^ , ⋯   , β k ^ ; x 1 , ⋯   , x n ) = m a x { p ( x 1 , ⋯   , x n ) ; β 1 , ⋯   , β k } L(hat{beta_1},cdots,hat{beta_k};x_1,cdots,x_n)=max{p(x_1,cdots,x_n);beta_1,cdots,beta_k} L(β1​^​,⋯,βk​^​;x1​,⋯,xn​)=max{p(x1​,⋯,xn​);β1​,⋯,βk​}
但是，使用极大似然估计必须已知总体的分布函数，而在时间序列分析中，序列总体分布通常是未知的。为了便于分析计算，通常假设序列服从多元正态分布。

独立的多元正态分布：

以上在理论上是可行的，但实际上上式存在p+q个超越方程，通常需要利用迭代法才能求出未知参数的极大似然估计值。实际操作中可以借助计算机。

4.3.3 最小二乘估计

在ARMA（p，q）模型场合，记
$$\begin{gathered} \tilde{\beta }=({\varphi }_1,\cdots ,{\varphi }_p,{\theta }_1,\cdots ,{\theta }_q{)}^{\prime } \\ {F}_t(\tilde{\beta })={\varphi }_1{x}_{t-1}+\cdots +{\varphi }_p{x}_{t-p}-{\theta }_1{ϵ}_{t-1}-\cdots -{\theta }_q{ϵ}_{t-q} \end{gathered}$$
残差项为：
$${ϵ}_t=x_t-F_t(\tilde{\beta })$$
残差平方和为：
$$\begin{gathered} Q(\tilde{\beta })=\sum _{t=1}^n{ϵ}_t^2 \\ =\sum _{t=1}^n(x_t-{\varphi }_1{x}_{t-1}+\cdots +{\varphi }_p{x}_{t-p}-{\theta }_1{ϵ}_{t-1}-\cdots -{\theta }_q{ϵ}_{t-q}{)}^2 \end{gathered}$$
使残差平方和达到最小的那组参数值即$\tilde{\beta }$的最小二乘估计。

在实际中，最常用的是条件最小二乘估计方法。它假定过去未观测到的序列值等于零，于是有
$${ϵ}_t=\frac{\Phi (B)}{\Theta (B)}{x}_t=x_t-\sum _{i=1}^t{\pi }_i{x}_{t-i}$$
于是残差平方和为：
$$\begin{gathered} Q(\tilde{\beta })=\sum _{t=1}^n{ϵ}_t^2 \\ =\sum _{t=1}^n[x_t-\sum _{i=1}^t{\pi }_i{x}_{t-i}{]}^2 \end{gathered}$$

4.4 模型检验

4.4.1 模型的显著性检验

模型的显著性检验主要是检验模型的有效性。且一个模型是否显著有效主要看它提取的信息是否充分。也即是残差项应该是白噪声序列。

4.4.2 参数的显著性检验

参数的显著性检验就是检验每一个未知参数是否显著非零。

4.5 模型优化

有时同一个序列可以有不同的拟合模型，且都显著有效，那么我们怎么选择呢？

这时就要用到AIC准则和SBC准则，即自小信息量准则，一般用软件拟合时会直接给出。
$$AIC=-2ln(模型的极大似然函数值)+2（模型中未知参数个数）$$
AIC准则的局限性在于受到样本容量的限制，当样本容量趋于无限大的时候，由AIC准则选择的模型不收敛于真实模型，它通常比真实模型所含的未知参数个数还要多。

BIC准则也称SBC准则弥补了这个不足。
$$SBC=-2ln(模型的极大似然函数值)+(lnn)（模型中未知参数个数）$$

4.6 序列预测

根据ARMA（p,q）模型的平稳性和可逆性，可以用传递形式和逆转形式等价描述该序列：
$$\begin{gathered} x_t=\sum _{i=0}^{\infty }{G}_i{ϵ}_{t-i} \\ {ϵ}_t=\sum _{j=0}^{\infty }{I}_j{x}_{t-j} \end{gathered}$$
其中 { G i } {G_i} {Gi​}是Green函数值； { I j } {I_j} {Ij​}为逆转函数值。

将两式合并，有
$$x_t=\sum _{i=0}^{\infty }\sum _{j=0}^{\infty }{G}_i{I}_j{x}_{t-i-j}$$
简记为
$$x_t=\sum _{i=0}^{\infty }{C}_i{x}_{t-1-i}$$
$\forall l⩾1$时，对任意未来t+l时刻，该时刻的序列值可以表示为它的历史数据$x_{t+l-1},\cdots ,x_{t+1},x_t,\cdots$的线性函数
$$x_{t+l}=\sum _{i=0}^{\infty }{C}_i{x}_{t+l-1-i}$$
但有趣的是$x_t$前的历史信息已知，$x_{t+1},\cdots ,x_{t+l-1}$期的信息是未知的，但根据线性函数的可加性，所有的未知历史信息都可以用已知历史信息的线性函数表示出来。

如$x_{t+2}={\sum }_{i=0}^{\infty }{C}_i{x}_{t+1-i}=C_0{x}_{t+1}+{\sum }_{i=0}^{\infty }{C}_{i+1}{x}_{t-i}$，但是因为$x_{t+1}$是未知的，而其又可以表示为$x_{t+1}={\sum }_{i=0}^{\infty }{C}_i{x}_{t-i}$，故有
$$x_{t+2}=\sum _{i=0}^{\infty }(C_0{C}_i+C_{i+1})x_{t-i}$$
由此$x_{t+2}$最终表示为已知历史信息$x_t,x_{t-1},\cdots$的线性函数。同理，对于未来任意l时刻的序列值$x_{t+l}$最终都可以用已知历史信息$x_t,x_{t-1},\cdots$表示出来，并将该线性函数形式记为：
$$\widehat{x_t}(l)=\sum _{i=0}^{\infty }{\hat{D}}_i{x}_{t-i}$$
${\hat{x}}_t(l)$也称为序列 { x t } {x_t} {xt​}的第l步预测值。

代码：

A7<-read.csv(“A1_7.CSV”)
A8<-read.csv(“A1_8.csv”)
A9<-read.csv(“A1_9.csv”)
a7<-ts(A7$number,start=1900,frequency=1)a8<-ts(A8$overshort,start = 1,frequency = 365)
a9<-ts(A9$change,start = 1880,frequency = 1)
a<-diff(a9,lag = 1)#对数据进行一阶差分

#install.packages(“aTSA”)
library(aTSA)
#class(A7)
adf.test(a7)#平稳性检验
acf(a7,lag=25)#绘制自相关图
acf(a7,lag=25)KaTeX parse error: Expected 'EOF', got '#' at position 4: acf#̲显示自相关系数 拖尾 pac…pacf#显示偏自相关系数 一阶截尾
plot(a8)
adf.test(a8)#ADF检验
Box.test(a8,lag = 6)
Box.test(a8,lag = 12)
for (k in 1:2) {print(Box.test(a8,lag = 6k,type = “Ljung-Box”))
}
acf(a8,lag=20)
pacf(a8)
plot(a9)
adf.test(a9)
plot(a)
acf(a)
pacf(a)
for (k in 1:2) {print(Box.test(a9,lag = 6k,type = “Ljung-Box”))
}
par(mfrow=c(1,2))
acf(a9)
pacf(a9)

###参数估计，使用函数arima（）拟合
fit1<-arima(a7,order = c(1,0,0),include.mean=T,method = “CSS-ML”)#极大似然估计与条件最小二乘估计混合
fit1
fit1<-arima(a7,order = c(1,0,0),method = “CSS”)
fit2<-arima(a8,order = c(0,0,1),method = “CSS”)#条件最小二乘估计
fit2
fit3<-arima(a,order = c(1,0,1))
fit3

#####模型检验，使用aTSA包中的ts.diag函数
library(aTSA)
ts.diag(fit1)#模型的显著性检验
t=abs(fit1$coef)/sqrt(diag(fit1$var.coef))
pt(t,length(a7)-length(fit1$coef),lower.tail = F)

###模型预测，使用forecast包中的forecast函数
install.packages(“forecast”)
#library(forecast)
forecast::forecast##因前面打开aTSA包
fore1<-forecast::forecast(fit1,h=10)
fore1
plot(fore1,lty=2)
lines(fore1$fitted,col=4)
未完…

最后

以上就是心灵美羽毛为你收集整理的第四章 平稳序列的拟合与预测第四章 平稳序列的拟合与预测的全部内容，希望文章能够帮你解决第四章 平稳序列的拟合与预测第四章 平稳序列的拟合与预测所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。