梯度消失、梯度爆炸产生的原因

92 阅读 0 评论 61 点赞

我是靠谱客的博主粗暴冷风，最近开发中收集的这篇文章主要介绍梯度消失、梯度爆炸产生的原因，觉得挺不错的，现在分享给大家，希望可以做个参考。

概述

一、梯度消失、梯度爆炸产生的原因
　　对于1.1 1.2，其实就是矩阵的高次幂导致的。在多层神经网络中，影响因素主要是权值和激活函数的偏导数。
1.1 前馈网络

若要对于w1求梯度，根据链式求导法则，得到的解为：

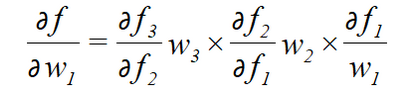
　　通常，若使用的激活函数为sigmoid函数，其导数最大为1/4：

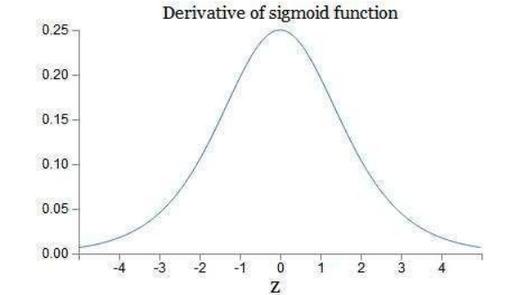
这样可以看到，如果我们使用标准化初始w，那么各个层次的相乘都是0-1之间的小数，而激活函数f的导数也是0-1之间的数，其连乘后，结果会变的很小，导致梯度消失。若我们初始化的w是很大的数，w大到乘以激活函数的导数都大于1，那么连乘后，可能会导致求导的结果很大，形成梯度爆炸。
　通常我们会将一个完整的句子序列视作一个训练样本，因此总误差即为各时间步（单词）的误差之和。
而RNN还存在一个权值共享的问题，即这几个w都是一个，假设，存在一个反复与w相乘的路径，t步后，得到向量：

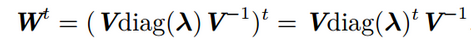
　　若特征值大于1，则会出现梯度爆炸，若特征值小于1，则会出现梯度消失。因此在一定程度上，RNN对比BP更容易出现梯度问题。主要是因为RNN处理时间步长一旦长了，W求导的路径也变的很长，即使RNN深度不大，也会比较深的BP神经网络的链式求导的过程长很大；另外，对于共享权值w，不同的wi相乘也在一定程度上可以避免梯度问题。
二、如何解决梯度消失、梯度爆炸
　　1、对于RNN，可以通过梯度截断，避免梯度爆炸
　　首先设置梯度阈值：clip_gradient
　　在后向传播中求出各参数的梯度，不直接用梯度进行参数更新，求梯度的L2范数
　　然后比较范数||g||与clip_gradient的大小
　　如果范数大，求缩放因子clip_gradient/||g||，由缩放因子可以看出梯度越大，缩放因子越小，就可以很好的控制梯度的范围。
　　最后将梯度乘以缩放因子得到最后需要的梯度。
　　L1范数是指向量中各个元素绝对值之和
L2范数是指向量各元素的平方和然后求平方根
　　2、可以通过添加正则项，避免梯度爆炸
　　正则化是通过对网络权重做正则限制过拟合，仔细看正则项在损失函数的形式：
regularization 公式：
Loss=(y−WTx)2+α∣∣W∣∣2,其中,α 是指正则项系数，因此，如果发生梯度爆炸，权值的范数就会变的非常大，通过正则化项，可以部分限制梯度爆炸的发生。
　　3、使用LSTM等自循环和门控制机制，避免梯度消失
　　4、优化激活函数，譬如将sigmold改为relu，避免梯度消失
　　如果激活函数的导数是1，那么就没有梯度爆炸问题了。可以发现，relu函数的导数在正数部分，是等于1的，因此就可以避免梯度消失的问题。【不好】：但是负数部分的导数等于0，这样意味着，只要在链式法则中某一个
小于0，那么这个神经元的梯度就是0，不会更新。
5、BN层
BN层提出来的本质就是为了解决反向传播中的梯度问题。
假设第一层的输入数据经过第一层的处理之后，得到第二层的输入数据。这时候，第二层的输入数据相对第一层的数据分布，就会发生改变，所以这一个batch，第二层的参数更新是为了拟合第二层的输入数据的那个分布。然而到了下一个batch，因为第一层的参数也改变了，所以第二层的输入数据的分布相比上一个batch，又不太一样了。然后第二层的参数更新方向也会发生改变。层数越多，这样的问题就越明显。
但是为了保证每一层的分布不变的话，那么如果把每一层输出的数据都归一化0均值，1方差不就好了？但是这样就会完全学习不到输入数据的特征了。不管什么数据都是服从标准正太分布，想想也会觉得有点奇怪。所以BN就是增加了两个自适应参数，可以通过训练学习的那种参数。这样把每一层的数据都归一化到β均值，γ标准差的正态分布上。
【将输入分布变成正态分布，是一种去除数据绝对差异，扩大相对差异的一种行为，所以BN层用在分类上效果的好的。
6、残差网络
残差单元可以以跳层连接的形式实现，即将单元的输入直接与单元输出加在一起，然后再激活。因此残差网络可以轻松地用主流的自动微分深度学习框架实现，直接使用BP算法更新参数。错误信号可以不经过任何中间权重矩阵变换直接传播到低层，一定程度上可以缓解梯度弥散问题（即便中间层矩阵权重很小，梯度也基本不会消失）。
三、梯度消失和梯度爆炸哪种经常出现
　　事实上，梯度消失更容易出现，因为对于激活函数的求导：
　　可以看到，当w越大，其wx+b很可能变的很大，而根据上面sigmoid函数导数的图像可以看到，wx+b越大，导数的值也会变的很小。因此，若要出现梯度爆炸，其w既要大还要保证激活函数的导数不要太小。