RNN的梯度消失问题

学习吴恩达老师的AI课程笔记，详细视频课程请移步https://mooc.study.163.com/smartSpec/detail/1001319001.htm

RNN模型结构：

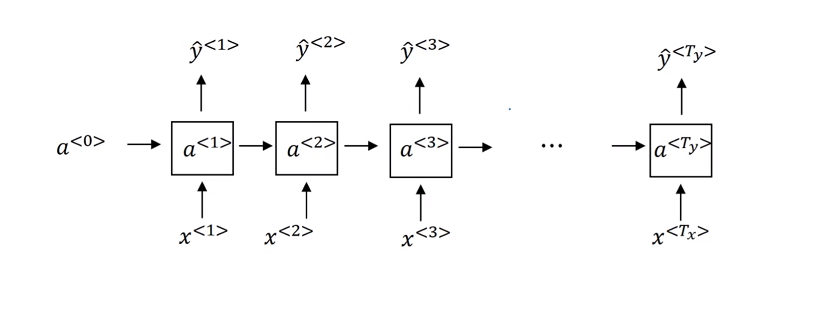
可以看出 如果说有一个非常长的句子（则对应会有一个非常深的网络）,这个句子中句尾的某个词严重受句首某些词的影响（英语中的单复数，时态），这时候由于网络非常的深，则在反向传播的过程中极易出现梯度消失或者梯度爆炸的情况（反向传播时）。
* 关于梯度消失的详细解释； --引自知乎 https://zhuanlan.zhihu.com/p/28687529

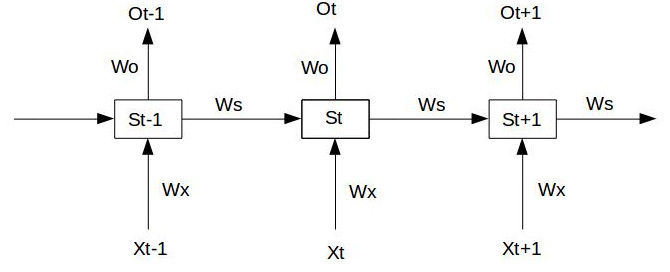
假设我们的时间序列只有三段S0为给定值，神经元没有激活函数，则RNN最简单的前向传播过程如下：
$$S_1=W_x{X}_1+W_s{S}_0+b_1，O_1=W_0{S}_1+b_2$$ $$S_2=W_x{X}_2+W_s{S}_1+b_1，O_2=W_0{S}_2+b_2$$ $$S_3=W_x{X}_3+W_s{S}_2+b_1，O_3=W_0{S}_3+b_2$$假设在t=3时刻，损失函数为$$L3=\frac{1}{2}(Y_3-O_3{)}^2$$。 则对于一次训练任务的损失函数为$$L=\sum _{t=0}^T{L}_t$$ ，即每一时刻损失值的累加。使用随机梯度下降法训练RNN其实就是对Wx、Ws、W0以及b1、b2求偏导，并不断调整它们以使L尽可能达到最小的过程。现在假设我们我们的时间序列只有三段，t1，t2，t3。我们只对t3时刻的Wx、Ws、W0求偏导（其他时刻类似）：$$\frac{\delta L_3}{\delta W_0}=\frac{\delta L_3}{\delta O_3}\frac{\delta O_3}{\delta W_0}$$ $$\frac{\delta L_3}{\delta W_x}=\frac{\delta L_3}{\delta O_3}\frac{\delta O_3}{\delta S_3}\frac{\delta S_3}{\delta W_x}+\frac{\delta L_3}{\delta O_3}\frac{\delta O_3}{\delta S_3}\frac{\delta S_3}{\delta S_2}\frac{\delta S_2}{\delta W_x}+\frac{\delta L_3}{\delta O_3}\frac{\delta O_3}{\delta S_3}\frac{\delta S_3}{\delta S_2}\frac{\delta S_2}{\delta S_1}\frac{\delta S_1}{\delta W_x}$$$$\frac{\delta L_3}{\delta W_s}=\frac{\delta L_3}{\delta O_3}\frac{\delta O_3}{\delta S_3}\frac{\delta S_3}{\delta W_s}+\frac{\delta L_3}{\delta O_3}\frac{\delta O_3}{\delta S_3}\frac{\delta S_3}{\delta S_2}\frac{\delta S_2}{\delta W_s}+\frac{\delta L_3}{\delta O_3}\frac{\delta O_3}{\delta S_3}\frac{\delta S_3}{\delta S_2}\frac{\delta S_2}{\delta S_1}\frac{\delta S_1}{\delta W_s}$$ 可以看出对于W0求偏导并没有长期依赖，但是对于Wx、Ws求偏导，会随着时间序列产生长期依赖。因为St随着时间序列向前传播，而St又是Wx、Ws的函数。根据上述求偏导的过程，我们可以得出任意时刻对Wx、Ws求偏导的公式：$$\frac{\delta L_t}{\delta W_x}=\sum _{k=0}^t\frac{\delta L_t}{\delta O_t}\frac{\delta O_t}{\delta S_t}(\bigcap _{j=k+1}^t\frac{\delta S_j}{\delta S_j-1})\frac{\delta S_k}{\delta W_x}$$任意时刻对Ws求偏导的公式同上。如果加上激活函数，$$S_j=tanh(W_x{X}_j+W_s{S}_{j-1}+b_1)$$，则$$\bigcap _{j=k+1}^t\frac{\delta S_j}{\delta S_j-1}=\bigcap _{j=k+1}^{t}tan{h}^{\prime }{W}_s$$解决方法：
*** 梯度爆炸：** 容易发现，对梯度设定一个最大的阈值，将梯度设定在阈值范围内
*** 梯度消失：**

    GRU: 

图中的C为记忆单元，他负责存储可能对后续字节有较大影响的字节，CN(t)则代表每步运行后的C值的候选值（是否需要把C值更新为候选值），Iu是门，用来决定是否需要更新，从上式c(t)可以看出 当lu为1是则代表需要更新，为0则无需更新。实际中的GRU 上述的各个环节都可能是多个元素的 如C(t)里可能有[a,b,c,d,e,g…]等100个元素，则Iu中对应的也应有100个元素[0,0,0,0,1,1,0,1,0…],两者的每个元素相对应，使得候选值被准确的定位是否需要更新。 完整的GRU

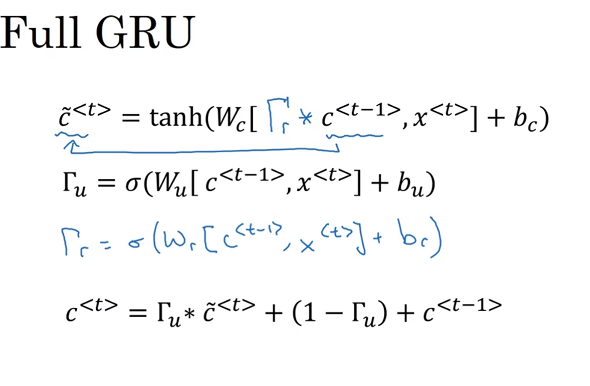
* LSTM：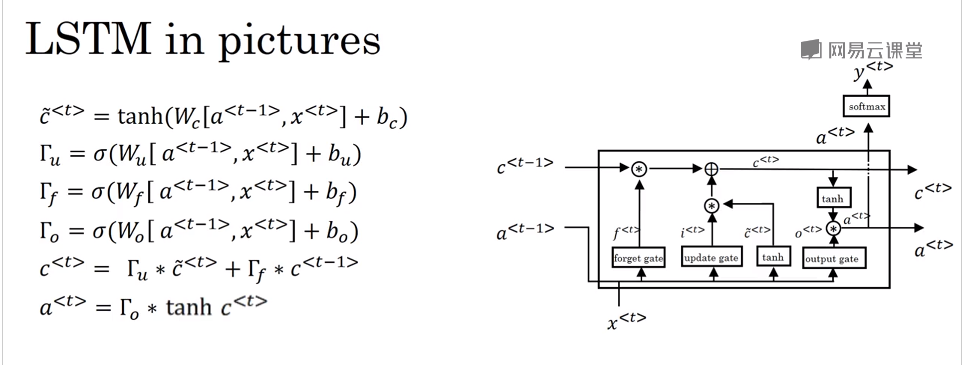
可以看看出LSTM有三个门控单元 分别是更新门Tu,Tf,To 对比GRU可以看出 更新值C(t)直接由更新门Tu和遗忘门Tf控制是否需要更新。

最后

以上就是从容樱桃最近收集整理的关于RNN的梯度消失问题的全部内容，更多相关RNN内容请搜索靠谱客的其他文章。