了解了当前深度学习的发展状况,就已经接近了机器学习的前沿领域。本章中,将通过目前被称为循环神经网络(Recurrent Neural Networks,RNN)的一系列算法,为机器学习模型加入一个非常特别的维度(时间,即输入序列)。
7.1 按顺序解决问题——RNN
在前面的章节中,介绍了一系列的模型,从简单到复杂,这些模型都有一些共同的属性。
- 接受唯一且独立的输入。
- 输出数据维度唯一并固定。
- 输出仅依赖于当前输入的特性,与过去或之前的输入无关。
现实中,大脑处理信息片段的过程具有内在的结构和顺序,人类感知到的现象结构和顺序也会影响信息的处理过程。类似的例子包括语言理解(单词在句子中的顺序)、视频序列(视频中帧的顺序),以及语言翻译。这些都促成了新模型的诞生。最重要的一部分模型都利用到了RNN。
7.1.1 RNN的定义
RNN是一种输入和输出都有相应序列的人工神经网络(Artificial Neural Network,ANN)。正式的定义可以描述如下。
“循环神经网络表示固定维度的高维向量序列(称为隐藏状态),通过复杂的非线性函数与新的观察值结合。”
RNN具有很强的表达性,能够进行任意存储大小的计算,因此,通过配置,RNN在复杂的序列处理任务上可以达到非常优秀的性能。
序列类型
无论在输入还是输出范畴内,RNN都要基于序列模型工作。因此,可以采用所有可能的序列组合来解决不同种类的问题。如图7.1所示,描述了目前使用的主要序列结构,后续递归循环也会参考这些结构。
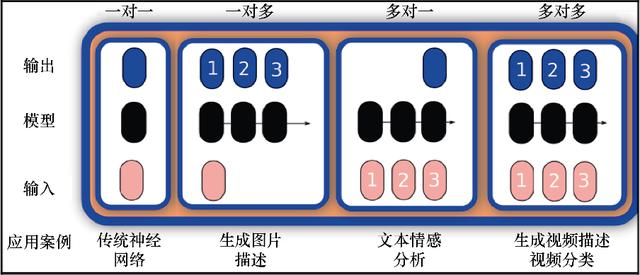
图7.1 序列模型的种类
7.1.2 RNN的发展
RNN的起源与其他现代神经网络惊人地相似,可以追溯到20世纪80年代的Hopfield网络,但其在20世纪70年代就已有所发展。
循环网络的迭代结构如图7.2所示。
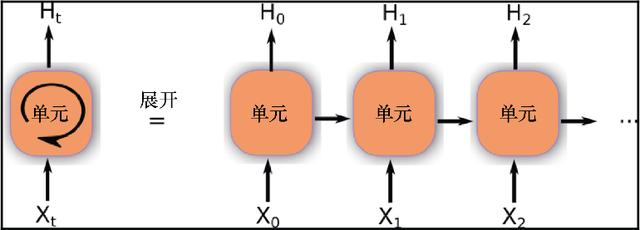
图7.2 循环网络单元展开
经典RNN节点拥有连接到自身的一个循环链接,因此,可以将权值作为输入序列的一部分。另外,在图7.2的右侧,可以看到展开后的网络基于内部的模型产生一系列的输出。将当前输入事件以激活的形式保存(短期记忆,与长期记忆相反,体现在权重的缓慢变化上)。这对很多应用有重要的潜在意义,包括语音处理、音乐合成(例如Mozer,1992)、自然语言处理(Natural Language Processing,NLP)以及其他众多领域。
1.训练方法——后向传播
在研究了相当数量的模型之后,有可能会观察到这些模型训练步骤的一些共有模式。
对循环神经网络来说,常用的损失最小化技术是著名的后向传播算法的变种,后向传播算法(Backpropagation Through Time,BPTT)采用将所有输入时间步展开的方式工作。每个时间步包括输入时间步、整个网络的一个副本、一个输出。计算并累加每个时间步的损失,最后将整个网络卷起,并更新权值。
从空间上看,循环神经网络展开后的每个时间步可以看作是单独的一层,每个时间步之间存在依赖关系,每个时间步的输出都是其下一个时间步的输入。这导致了复杂的训练性能需求,因此,诞生了时间截断的反向传播算法。
下面的伪代码描述了整个过程。
Unfold the network to contain k instances of the cell
While (error < ε or iteration>max):
x = zeros(sequence_legth)
for t in range (0, n-sequence_length) # initialize the weights
copy sequence_length input values into the input x
p = (forward-propagate the inputs over the whole unfolded
network)
e = y[t+k] - p; # calculate error as target
- prediction
Back-propagate the error e, back across the whole unfolded
network
Sum the weight changes in the k model instances together.
Update all the weights in f and g.
x = f(x, a[t]); # compute new input for the next
time- step2.传统RNN的主要问题——梯度爆炸和消失
事实证明,训练RNN网络是很困难的,特别是对复杂的长距离问题——通过正确的配置,RNN或许是最有用的。由于潜在优势还未发挥出来,因此解决RNN训练难度的方法就显得尤为重要。
目前广泛用于学习短期记忆输入内容的算法需要耗费大量的时间,有时甚至无法工作,特别当输入和相应信号的最小时间间隔很长时。虽然理论上很迷人,但通过传统前向网络,现有的方法在实践中没有优势。
RNN的一个主要问题出现在后向传播阶段。考虑到其循环特性,损失后向传播的步数相当于一个深度非常深的网络。这种梯度的级联计算可能会导致在最后阶段梯度值非常小,或者相反,导致参数漫无边界的不断增大。这种现象被称为梯度消失和爆炸。这也是导致产生LSTM的原因之一。
传统BPTT的问题是损失信号在后向传播过程中要么爆炸式增加,要么消失——后向传播损失随着时间的变化指数性地依赖于权值大小。这有可能会导致权值振荡,或者耗费大量时间,甚至根本无法工作。
为解决梯度消失或爆炸问题,研究者进行了大量不同的尝试,最终在1997年,Schmidhuber和Sepp发布了一篇关于RNN和LSTM的基础研究论文,为这一领域的发展铺平了道路。
7.2 LSTM
LSTM是RNN的基本步骤,它将长期依赖性地引入RNN单元。展开后的单元包括两种不同的参数:一种是长期状态,另一种表示短期记忆。
每步之间,长期状态会遗忘不太重要的信息,同时增加经过过滤的来自短期记忆的事件信息,并将两者结合后输出到后续步骤。
LSTM在其可能的应用中是非常灵活的,与GRU一样,都是被广泛应用的循环模型,GRU将在后面介绍。为方便理解LSTM的工作过程,下面会将其按组成单元进行分解。
7.2.1 门和乘法运算
LSTM有两类基本的功能:记住当前重要的事情,缓慢遗忘过去不重要的事情。有哪种机制可以实现这种过滤功能?这种运算被称为门运算。
门运算的基本元素包括一个多元向量和一个过滤向量,过滤向量与输入值点乘,以允许或拒绝某些输入元素被传输。如何调整门过滤器呢?这个多元控制向量(在图7.3中用箭头表示)通过sigmoid激活函数与神经网络层相连。控制向量通过sigmoid激活函数后将产生类似二进制的输出。
在图7.3中,用一系列开关表示门。
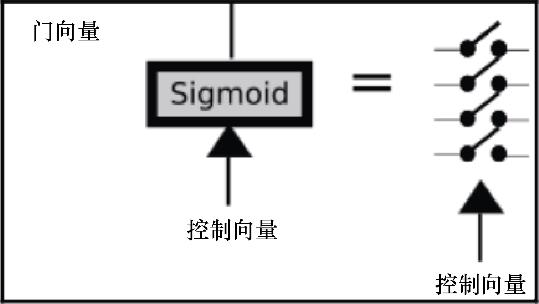
图7.3 LSTM门
此过程中另外一个重要的部分是乘法运算,将训练过的过滤器正规化,将输入与门向量相乘。图7.4中的箭头图标表示过滤后的信号传输方向。
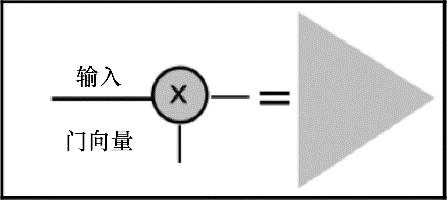
图7.4 门相乘运算
下面进一步具体讲述LSTM各单元的细节。
LSTM包含3个门,用于保护和控制单元状态:一个位于数据流的起始位置,另一个位于中间,最后一个位于单元信息边界的尾部。这个运算过程允许丢弃低重要性(期望不重要)的状态数据,并将新的数据(期望重要)与当前状态结合。
图7.5显示了LSTM单元内部运算的概念。以下信息将被作为输入。
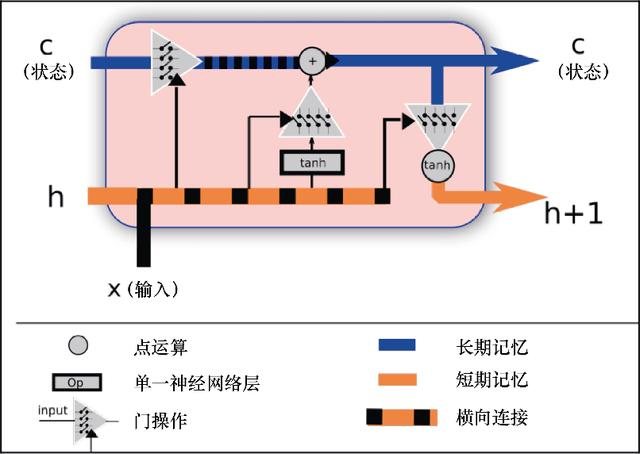
图7.5 LSTM单元及其组件
- 单元状态,保存有长期信息,因为其装载了自初始单元以来的训练优化后的权值。
- 短期状态,h(t),在每次迭代时直接与当前状态结合,所以对最新的输入值有重要影响。
下面,介绍LSTM单元的数据流,以便更好地理解LSTM单元中不同的门和运算是如何协同工作的。
7.2.2 设置遗忘参数(输入门)
在这一阶段,将来自短期记忆的值和输入结合(见图7.6),结果输出给一个用多变量Sigmoid函数表示的二进制函数。根据输入和短期记忆值,Sigmoid函数会过滤掉用单元状态权值表示的长期知识。
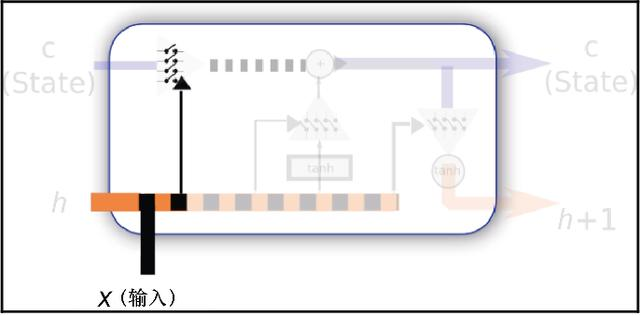
图7.6 状态遗忘参数设置
7.2.3 设置保持参数
下面通过设置过滤器,允许或拒绝新数据与短期记忆结合后的值进入单元的半永久状态,如图7.7所示。
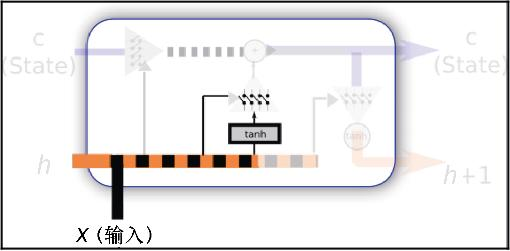
图7.7 短期值选择性设置
在这一阶段,将决定多少全新和半新的信息结合并进入单元新的状态。
7.2.4 修改单元
在序列的这一部分,通过配置过的信息过滤器传输相关信息,最终将得到更新后的长期状态值。
为了将新的信息和短期信息归一化,将新的输入和短期状态通过tanh激活函数输入神经网络。这将确保输入的新信息归一化到[−1,1]范围,如图7.8所示。
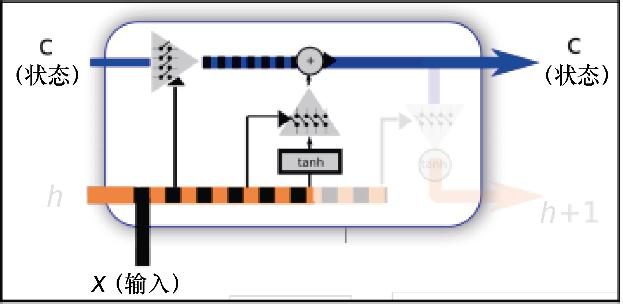

图7.8 状态持续改变的过程
7.2.5 输出过滤后的单元状态
接下来介绍短期状态。这里也需要用到经过新数据和之前的短期状态配置的过滤器,长期状态可以通过过滤器与tanh函数点乘,再次将信息归一化到[−1,1]的范围内,如图7.9所示。
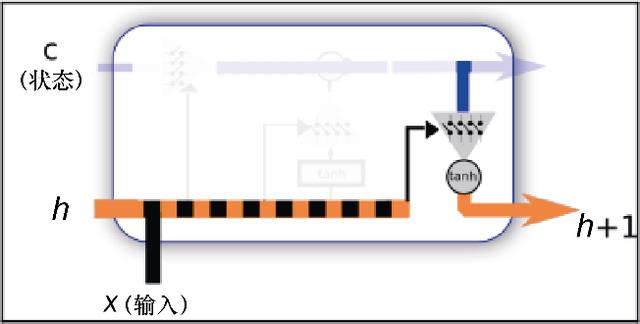
图7.9 新的短期状态产生过程
7.3 采用电能消耗数据预测单变量时间序列
在接下来的例子中,将解决回归领域的一个问题。因此,使用两个LSTM创建一个多层RNN。即将进行的回归类型属于多对一型,因为网络将收到电能消耗的数据序列,并尝试基于前面4个记录数据预测接下来的值。
本案例中采用的数据集来自一个家庭某段时间的电能消耗记录。可以推断,家庭电能消耗有很多规律可以遵循(比如居住者采用微波炉准备早餐以及整天使用计算机时,电能消耗将增加。下午会有一点下降,然后晚上会增加,因为所有灯都会打开,最后在零点左右开始下降,因为这时居住者已经休息了)。
首先加载必要的库文件,并初始化相应的环境变量,代码如下。
%matplotlib inline
%config InlineBackend.figure_formats = {'png', 'retina'}
import numpy as np
import pandas as pd
import tensorflow as tf
from matplotlib import pyplot as plt
from keras.models import Sequential
from keras.layers.core import Dense, Activation
from keras.layers.recurrent import LSTM
from keras.layers import Dropout
Using TensorFlow backend.数据集的描述和加载
本例中,使用电力负荷图数据集(Electricity Load Diagrams Data Sets),数据来自Artur Trindade。下面是原始数据集的描述。
“数据集没有缺失值。
“数据是每15分钟的kW值。除以4可以将数据转换为kWh数据。每列代表一个客户。有些客户是2011年之后创建的。这种情况下,将之前的电能消耗数据默认为是0。
“所有时间标签为葡萄牙的小时数。每天有96条记录(24×15)。每年3月份时间切换日(这一天只有23小时),上午1:00~2:00之间的所有记录为0。每年十月也是时间切换日(这一天有25小时),上午1:00~2:00之间的电能消耗按2个小时统计。”
为简化模型描述,采用一个客户完整的测量数据,并将其转换成标准的CSV格式。数据位于本章代码目录下的data子目录。
因此,首先从数据集中加载同一个家庭的1 500条电能消耗记录。
df = pd.read_csv("data/elec_load.csv", error_bad_lines=False)
plt.subplot()
plot_test, = plt.plot(df.values[:1500], label='Load')
plt.legend(handles=[plot_test])图7.10显示了即将应用于模型的数据子集。
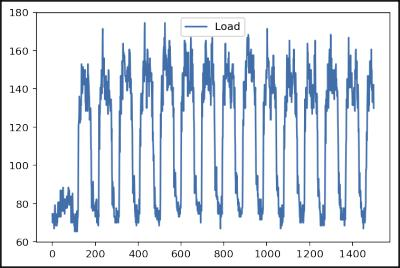
图7.10 前1 500条样本数据
查看这些数据的图示(采用了最开始的1 500条样本),可以看到初始的状态,这可能是刚开始测量时的记录值,然后可以看到清晰的电能消耗的高低周期变化。通过简单的观察,可以看到每个周期大致有100条记录,非常接近数据集所拥有的每天96条记录。
数据集预处理
为了确保后向传播算法能更好地覆盖数据集,需要将输入数据归一化。采用经典的缩放和对中技术,减去平均值,并使用最大值的floor()函数对数据缩放。使用Pandas的describe()方法得到需要的值。
print(df.describe())
array=(df.values - 145.33) /338.21
plt.subplot()
plot_test, = plt.plot(array[:1500], label='Normalized Load')
plt.legend(handles=[plot_test])
Load
count 140256.000000
mean 145.332503
std 48.477976
min 0.000000
25% 106.850998
50% 151.428571
75% 177.557604
max 338.218126图7.11所示为归一化后的数据。
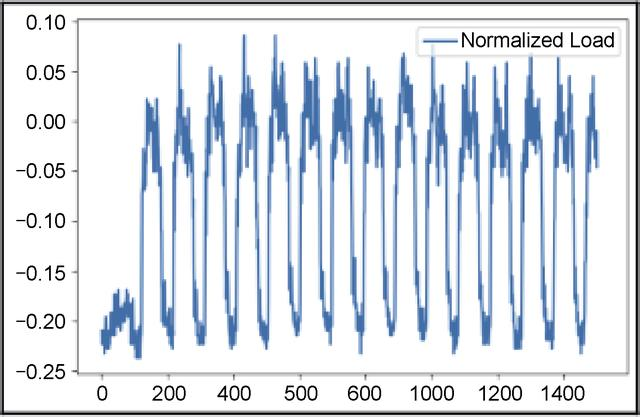
图7.11 归一化后的数据
在这一步中,将准备输入数据集,需要输入值x(前面5个值)以及对应的输入值y(5个时间步后的值)。然后,将其中13 000个数据分配给训练数据集,将随后的1 000个样本分配给测试集。
listX = []
listy = []
X={}
y={}
for i in range(0,len(array)-6):
listX.append(array[i:i+5].reshape([5,1]))
listy.append(array[i+6])
arrayX=np.array(listX)
arrayy=np.array(listy)
X['train']=arrayX[0:13000]
X['test']=arrayX[13000:14000]
y['train']=arrayy[0:13000]
y['test']=arrayy[13000:14000]下面开始创建模型,模型拥有两个LSTM和一个位于最后的dropout层。
#Build the model
model = Sequential()
model.add(LSTM( units=50, input_shape=(None, 1), return_sequences=True))
model.add(Dropout(0.2))
model.add(LSTM( units=200, input_shape=(None, 100),
return_sequences=False))
model.add(Dropout(0.2))
model.add(Dense(units=1))
model.add(Activation("linear"))
model.compile(loss="mse", optimizer="rmsprop")运行模型并调整权值。模型将使用数据集中8%的数据作为验证集。
#Fit the model to the data
model.fit(X['train'], y['train'], batch_size=512, epochs=10,
validation_split=0.08)
Train on 11960 samples, validate on 1040 samples
Epoch 1/10
11960/11960 [==============================] - 41s - loss: 0.0035 -
val_loss: 0.0022
Epoch 2/10
11960/11960 [==============================] - 61s - loss: 0.0020 -
val_loss: 0.0020
Epoch 3/10
11960/11960 [==============================] - 45s - loss: 0.0019 -
val_loss: 0.0018
Epoch 4/10
11960/11960 [==============================] - 29s - loss: 0.0017 -
val_loss: 0.0020
Epoch 5/10
11960/11960 [==============================] - 30s - loss: 0.0016 -
val_loss: 0.0015
Epoch 6/10
11960/11960 [==============================] - 28s - loss: 0.0015 -
val_loss: 0.0013
Epoch 7/10
11960/11960 [==============================] - 43s - loss: 0.0014 -
val_loss: 0.0012
Epoch 8/10
11960/11960 [==============================] - 37s - loss: 0.0013 -
val_loss: 0.0013
Epoch 9/10
11960/11960 [==============================] - 31s - loss: 0.0013 -
val_loss: 0.0012
Epoch 10/10
11960/11960 [==============================] - 25s - loss: 0.0012 -
val_loss: 0.0011
<keras.callbacks.History at 0x7fa435512588>重新调整后,查看模型预测的值,与真实值比较,真实值并没有参与模型训练,进一步理解模型是如何预测并生成样本家庭的行为的。
# Rescale the test dataset and predicted data
test_results = model.predict( X['test'])
test_results = test_results * 338.21 + 145.33
y['test'] = y['test'] * 338.21 + 145.33
plt.figure(figsize=(10,15))
plot_predicted, = plt.plot(test_results, label='predicted')
plot_test, = plt.plot(y['test'] , label='test');
plt.legend(handles=[plot_predicted, plot_test]);图7.12所示为最终经回归后的数据。
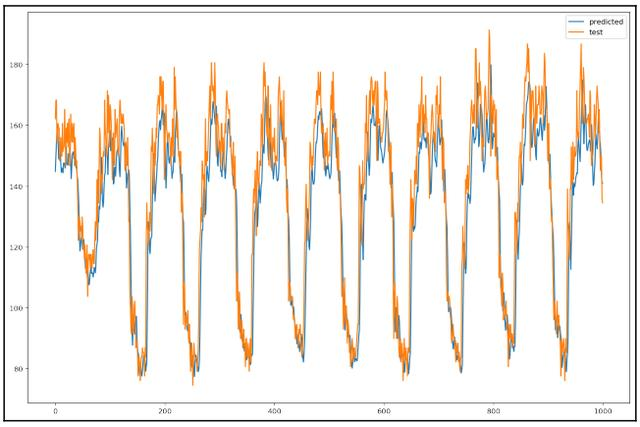
图7.12 最终经回归后的数据
7.4 小结
在本章中,视野进一步得到扩展,将时间这一重要维度添加到泛化的元素中。基于真实数据,学习了如何应用RNN解决实际的问题。
如果读者已经掌握了所有可能的选项,也可以进一步了解很多种类的模型。
在随后的章节中,将讨论其他重要的架构,这些架构经过训练,可用于生成更聪明的元素,例如,将著名画家的风格转移到一幅图片上,甚至玩视频游戏!请继续阅读后续关于强化学习和生成对抗网络的章节。
本文摘自《机器学习开发者指南》。

本书将带领读者学习如何实施各种机器学习技术及其日常应用的开发。本书分为9章,从易于掌握的语言基础数据和数学模型开始,向读者介绍机器学习领域中使用的各种库和框架,然后通过有趣的示例实现回归、聚类、分类、神经网络等,从而解决如图像分析、自然语言处理和时间序列数据的异常检测等实际问题。
最后
以上就是正直鸡翅最近收集整理的关于如何应用循环神经网络-RNN解决实际的问题的全部内容,更多相关如何应用循环神经网络-RNN解决实际内容请搜索靠谱客的其他文章。








发表评论 取消回复