RNN梯度消失和爆炸的原因

  一个经典的RNN结构如下图所示：
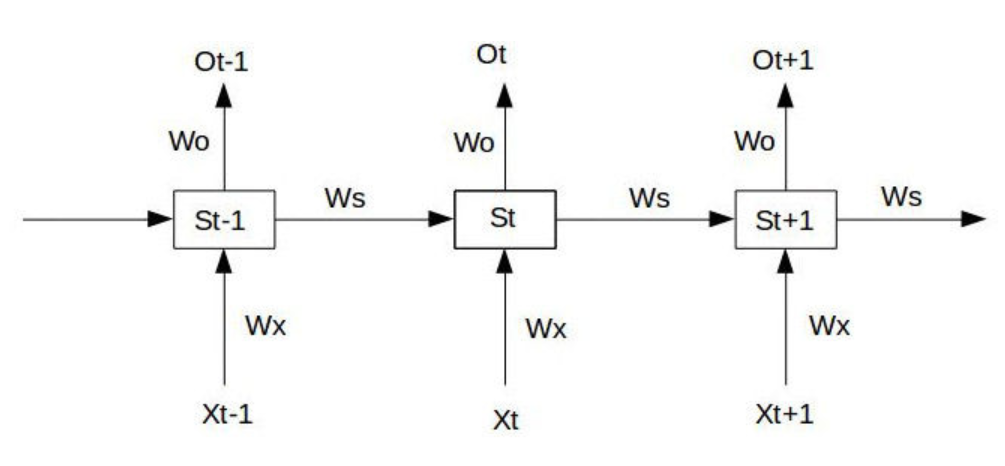  假设我们的时间序列只有三段， $S_0$为给定值，神经元没有激活函数，则RNN最简单的前向传播过程如下:$$S_1=W_x{X}_1+W_s{S}_0+b_1{O}_1=W_o{S}_1+b_2$$$$S_2=W_x{X}_2+W_s{S}_1+b_1{O}_2=W_o{S}_2+b_2$$$$S_3=W_x{X}_3+W_s{S}_2+b_1{O}_3=W_o{S}_3+b_2$$  假设在t=3时刻，损失函数为$L_3=\frac{1}{2}{\left(Y_3-O_3\right)}^2$。则对于一次训练任务的损失函数为$$L=\sum _{t=0}^T{L}_t$$即每一时刻损失值的累加。使用随机梯度下降法训练RNN其实就是对$W_x$、$W_s$、$W_o$ 以及$b_1$、$b_2$求偏导，并不断调整它们以使$L$尽可能达到最小的过程。现在假设我们我们的时间序列只有三段，$t_1$，$t_2$，$t_3$。我们只对$t_3$时刻的$W_x$、$W_s$、$W_o$ 求偏导（其他时刻类似）：$$\frac{\partial L_3}{\partial W_0}=\frac{\partial L_3}{\partial O_3}\frac{\partial O_3}{\partial W_o}$$$$\frac{\partial L_3}{\partial W_x}=\frac{\partial L_3}{\partial O_3}\frac{\partial O_3}{\partial S_3}\frac{\partial S_3}{\partial W_x}+\frac{\partial L_3}{\partial O_3}\frac{\partial O_3}{\partial S_3}\frac{\partial S_3}{\partial S_2}\frac{\partial S_2}{\partial W_x}+\frac{\partial L_3}{\partial O_3}\frac{\partial O_3}{\partial S_3}\frac{\partial S_3}{\partial S_2}\frac{\partial S_2}{\partial S_1}\frac{\partial S_1}{\partial W_x}$$$$\frac{\partial L_3}{\partial W_s}=\frac{\partial L_3}{\partial O_3}\frac{\partial O_3}{\partial S_3}\frac{\partial S_3}{\partial W_s}+\frac{\partial L_3}{\partial O_3}\frac{\partial O_3}{\partial S_3}\frac{\partial S_3}{\partial S_2}\frac{\partial S_2}{\partial W_s}+\frac{\partial L_3}{\partial O_3}\frac{\partial O_3}{\partial S_3}\frac{\partial S_3}{\partial S_2}\frac{\partial S_2}{\partial S_1}\frac{\partial S_1}{\partial W_s}$$
  可以看出对于 $W_o$ 求偏导并没有长期依赖，但是对于$W_x$、$W_s$求偏导，会随着时间序列产生长期依赖。因为 $S_t$ 随着时间序列向前传播，而$S_t$又是 $W_x$、$W_s$的函数。
  根据上述求偏导的过程，我们可以得出任意时刻对 $W_x$、$W_s$求偏导的公式：$$\frac{\partial L_t}{\partial W_x}=\sum _{k=0}^t\frac{\partial L_t}{\partial O_t}\frac{\partial O_t}{\partial S_t}\left(\prod _{j=k+1}^t\frac{\partial S_j}{\partial S_{j-1}}\right)\frac{\partial S_k}{\partial W_x}$$任意时刻对$W_s$ 求偏导的公式同上。
  如果再加上激活函数:$S_j=\tanh \left(W_x{X}_j+W_s{S}_{j-1}+b_1\right)$。其中${\tanh }^{\prime }=[0,1]$$$f(z)=\tanh (z)$$$$f(z{)}^{\prime }=1-(f(z){)}^2$$激活函数tanh和它的导数图像如下：
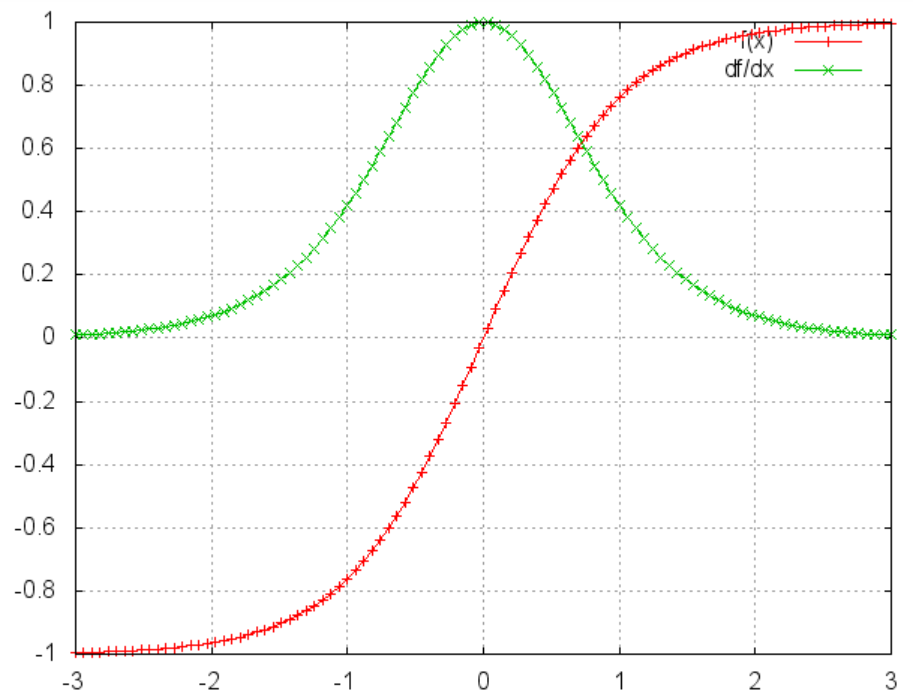  由上图可以看出${\tanh }^{\prime }\le 1$，对于训练过程大部分情况下tanh的导数是小于1的，因为很少情况下会出现$$W_x{X}_j+W_s{S}_{j-1}+b_1=0$$，如果$W_s$也是一个大于0小于1的值，则当$t$很大时$$\prod _{j=k+1}^t{\tanh }^{\prime }{W}_s$$会趋于0，和$0.01^{50}$趋近于0是一个概念，同理当$W_s$很大时，${\prod }_{j=k+1}^t{\tanh }^{\prime }{W}_s$会趋于无穷。这就是RNN中梯度消失和爆炸的原因。

  至于怎么避免这种现象，让我在看看就是$$\frac{\partial L_t}{\partial W_x}=\sum _{k=0}^t\frac{\partial L_t}{\partial O_t}\frac{\partial O_t}{\partial S_t}\left(\prod _{j=k+1}^t\frac{\partial S_j}{\partial S_{j-1}}\right)\frac{\partial S_k}{\partial W_x}$$梯度消失和爆炸的根本原因就是$$\prod _{j=k+1}^t\frac{\partial S_j}{\partial S_{j-1}}$$这一坨，要消除这种情况就需要把这一坨在求偏导的过程中去掉，至于怎么去掉，一种办法就是使 $$\frac{\partial S_j}{\partial S_{j-1}}\approx 1或者\frac{\partial S_j}{\partial S_{j-1}}\approx 0$$其实这就是LSTM做的事情。

总结：

  梯度消失：一句话，RNN梯度消失是因为激活函数tanh函数的倒数在0到1之间，反向传播时更新前面时刻的参数时，当参数W初始化为小于1的数，则多个(tanh函数’ * W)相乘，将导致求得的偏导极小（小于1的数连乘），从而导致梯度消失。
  梯度爆炸：当参数初始化为足够大，使得tanh函数的导数乘以W大于1，则将导致偏导极大（大于1的数连乘），从而导致梯度爆炸。

最后

以上就是甜美乐曲为你收集整理的RNN梯度消失和爆炸的原因的全部内容，希望文章能够帮你解决RNN梯度消失和爆炸的原因所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。