错排数问题

有 n 个箱子，颜色分别为 $1\cdots n$ 还有 n 个球，颜色也分别为 $1\cdots n$。现在要将每一个球分别放入一个箱子里，并且一个箱子里只能放一个球。
试求有多少种方案满足：每个箱子，和它里面球的颜色，都不一样。（如下图，虚线表示一个球不能放进箱子里）

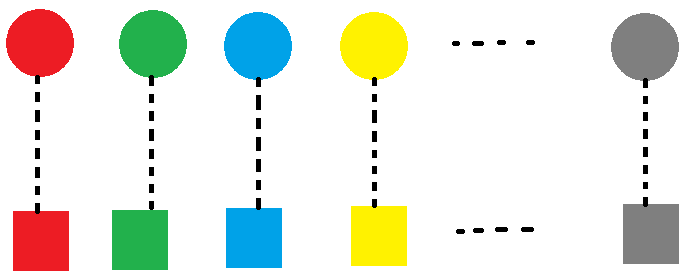
递推式

  我们假设 n 个球和 n 个箱子的错排数为 $D_n$。我们很容易算出来， $D_1=0，D_2=1，D_3=2$，然后 $D_4$ 就不是那么好算了。于是我们讨论 $D_n(n\in [4,\infty ))$ 到底等于多少。但是这个改如何讨论呢，似乎完全没有切入点。所以我们先看看能不能从题目中得到什么信息。题目中说颜色相同的球和箱子不能匹配，对应在我们这里就是说一个颜色为 $colo{r}_m$ 的球，不能放在颜色为 $colo{r}_m$ 的箱子里。也就是说，这个颜色为 $colo{r}_m$ 的球可以放在颜色为 $colo{r}_1，colo{r}_2，\cdots colo{r}_{m-1}，colo{r}_{m+1}，\cdots ，colo{r}_n$ 的箱子里。据此，我们就可以开始分类讨论（n- 1 类）了：

1. 把颜色为 $colo{r}_m$ 的球放进颜色为 $colo{r}_1$ 的箱子里。
2. 把颜色为 $colo{r}_m$ 的球放进颜色为 $colo{r}_2$ 的箱子里。
3. 把颜色为 $colo{r}_m$ 的球放进颜色为 $colo{r}_3$ 的箱子里。
   $⋮$

m-1. 把颜色为 $colo{r}_m$ 的球放进颜色为 $colo{r}_{m-1}$ 的箱子里。
m.     ,,, 把颜色为 $colo{r}_m$ 的球放进颜色为 $colo{r}_{m+1}$ 的箱子里。
   $⋮$
n-1.   , 把颜色为 $colo{r}_m$ 的球放进颜色为 $colo{r}_n$ 的箱子里。

  我们显然不能每一种情况都去讨论，因为情况数量太大了，所以我们在所有情况中找出一种情况讨论：把颜色为 $colo{r}_m$ 的球放进颜色为 $colo{r}_k$ 的箱子里。（如下图）

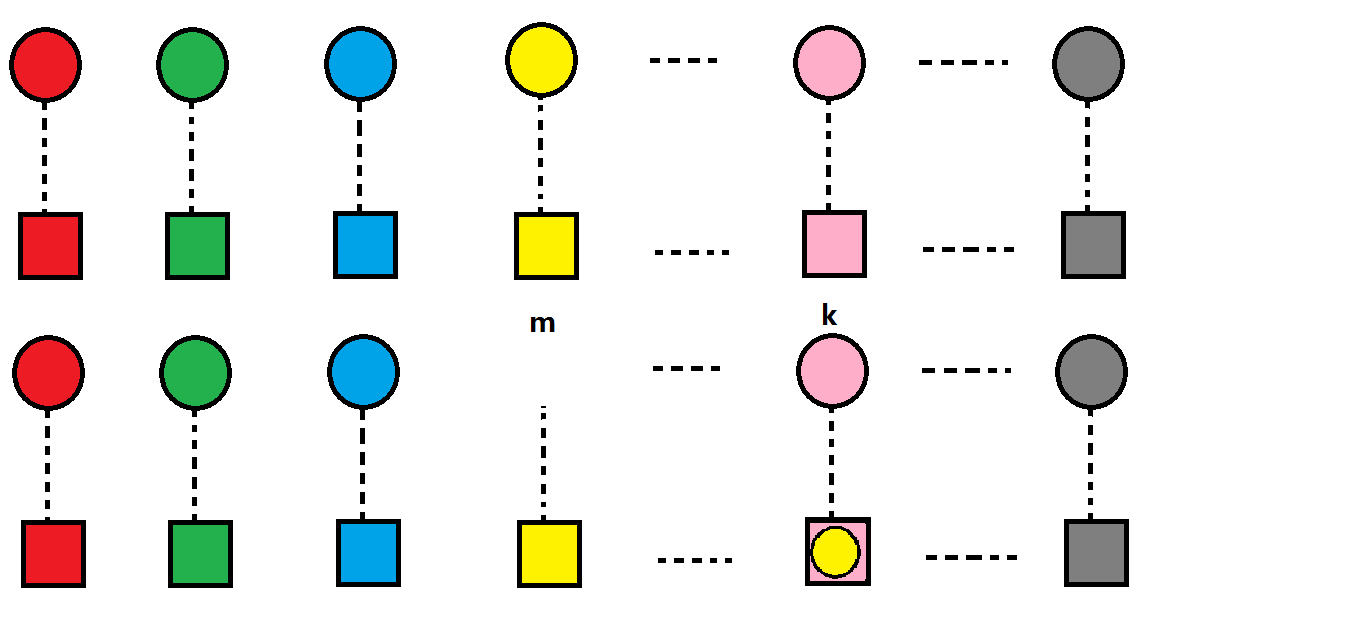
  现在又怎么办呢，既然颜色为 $colo{r}_k$ 的箱子已经被放进去了，那么颜色为 $colo{r}_k$ 的球对于剩下的所有箱子来说都是可以选择的。但是，对于剩下所有的箱子来说，有一个箱子是比较特殊的，那就是颜色为 $colo{r}_m$ 的箱子，因为与其他的箱子不同的是，它所对应的的球已经放到别的箱子里去了。所以我们据此又可以将这种情况又细分为下面两种更小的情况：

1. 颜色为 $colo{r}_k$ 的球放进了颜色为 $colo{r}_m$ 的箱子里。
2. 颜色为 $colo{r}_k$ 的球放没有放进颜色为 $colo{r}_m$ 的箱子里。

  我们先看第一种，就是下图所表现的这样：

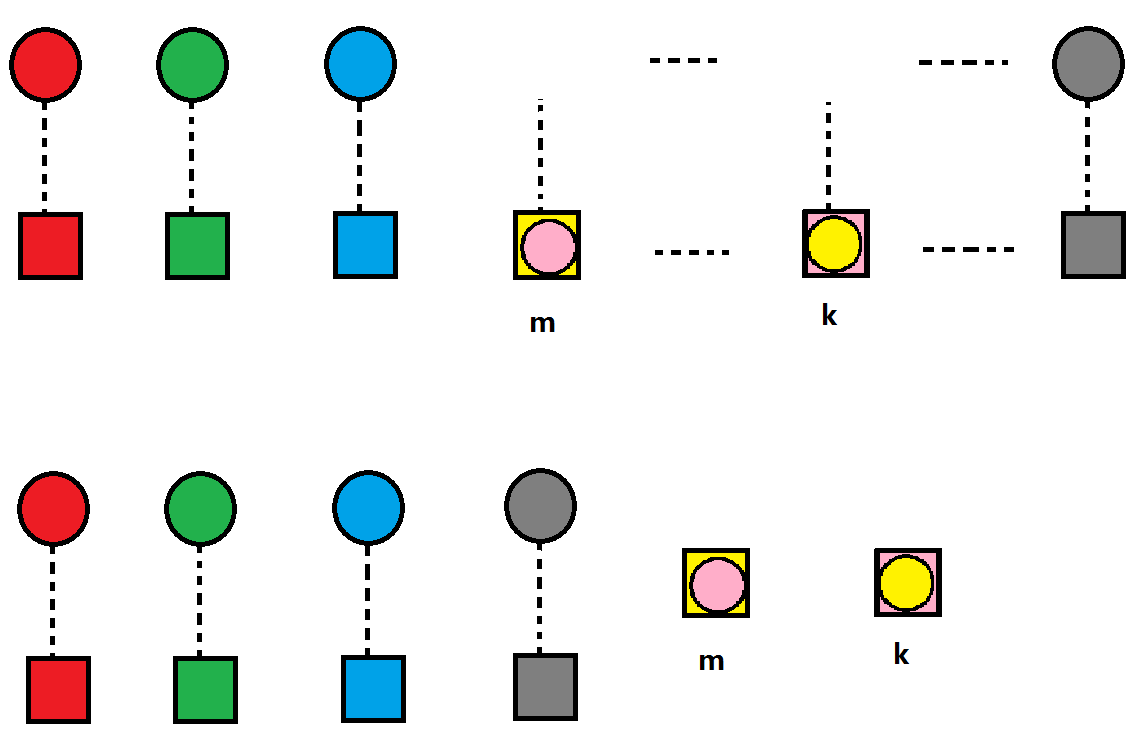
  很明显，这种情况中，剩下的所有球又构成了一个错排数问题，只不过这一次的问题规模减小了，变成了 n - 2。所以在这种情况中，所有排列的方案数也就是 $D_{n-2}$。
  然后是第二种情况：$colo{r}_k$ 的球放没有 放进颜色为 $colo{r}_m$ 的箱子里 。对于这一种情况，我们是不是可以换一种说法，把它变为：$colo{r}_k$ 的球放不能 放进颜色为 $colo{r}_m$ 的箱子里。 这个转换应该比较好理解，用图表示出来就是这样：

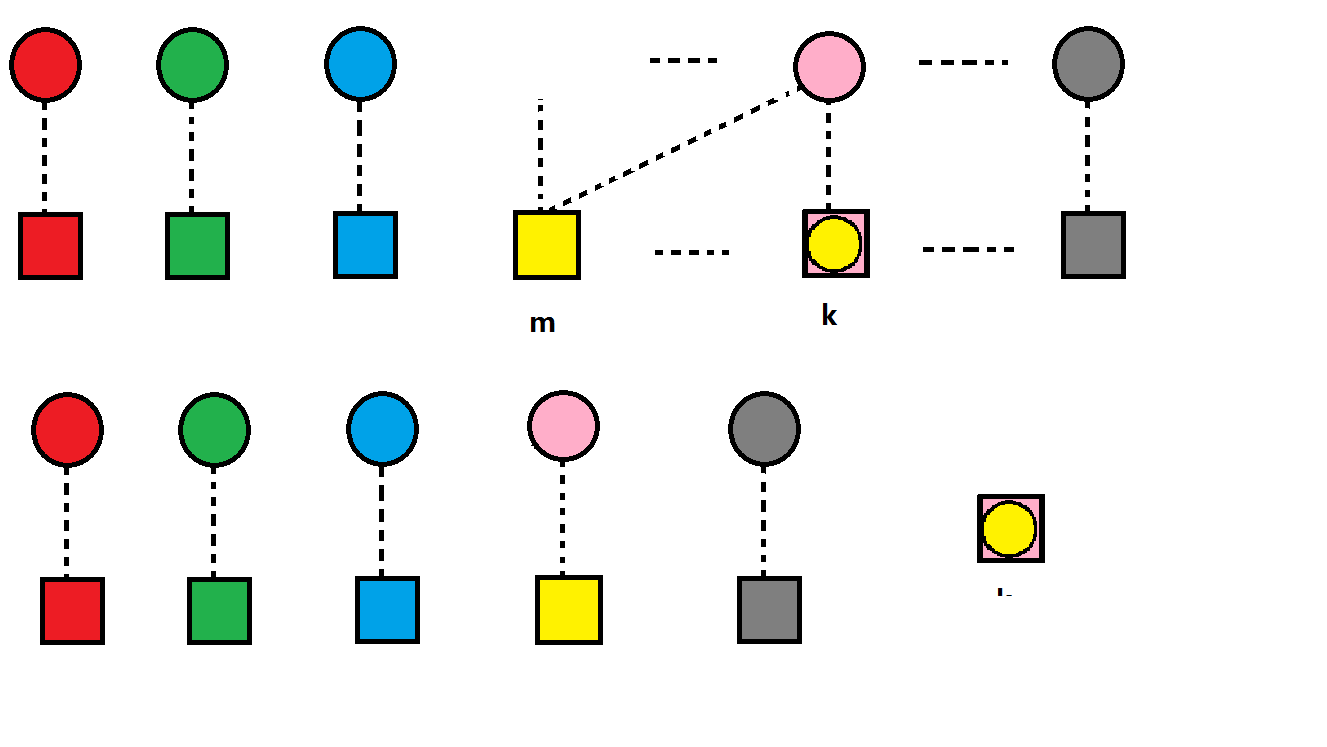
  也很明显的，我们知道这种情况下，剩下的球和箱子构成了一个规模为 n - 1，的错排数问题，所以这总情况下的总排列数为 $D_{n-1}$。
  综上所述，有根据加法原理，我们可以得到把颜色为 $colo{r}_m$ 的球放进颜色为 $colo{r}_k$ 的箱子里的总排列数为：$D_{n-2}+D_{n-1}$。又因为我们在分析这种情况的时候没有用到具体的 k 和 m，所以在这种情况的分析可以推广到所有的情况，也就是说我们在开头列出的 n - 1 种情况里的排列数都是 $D_{n-2}+D_{n-1}$。所以又一次根据加法原理，我们得到了：
$$D_n=(n-1)(D_{n-2}+D_{n-1})$$

通项公式

 推导过程太麻烦了直接写出公式 其实就是懒 ：
$$D_n=n![\frac{1}{2!}-\frac{1}{3!}+\cdots +(-1{)}^n\frac{1}{n!}]=n!\sum _{i=2}^n(-1{)}^n\frac{1}{i!}$$

最后

以上就是小巧野狼为你收集整理的关于错排数问题错排数问题的全部内容，希望文章能够帮你解决关于错排数问题错排数问题所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。