我自己在学这些数据结构以及算法的时候，网上的博客很多都是给出一个大致思想，然后就直接给代码了，可能是我智商太低，思维跳跃没有那么大，没法直接代码实现，而且有些学完之后也没有得到深层次的理解和运用，还是停留在只会使用模板的基础上。所以我希望我写的东西能让更多的人看明白，我会尽量写详细，也会写出我初学的时候哪些地方没有理解或者难以运用，又是怎样去熟练的使用这些东西的。可能还是不能让所有的人都读明白，但我尽量做的更好。

一、什么是线段树？

• 线段树是怎样的树形结构?

　　线段树是一种二叉搜索树，什么叫做二叉搜索树，首先满足二叉树，每个结点度小于等于二，即每个结点最多有两颗子树，何为搜索，我们要知道，线段树的每个结点都存储了一个区间，也可以理解成一个线段，而搜索，就是在这些线段上进行搜索操作得到你想要的答案。

• 线段树能够解决什么样的问题。

　　线段树的适用范围很广，可以在线维护修改以及查询区间上的最值，求和。更可以扩充到二维线段树（矩阵树）和三维线段树（空间树）。对于一维线段树来说，每次更新以及查询的时间复杂度为O(logN)。

• 线段树和其他RMQ算法的区别

　　常用的解决RMQ问题有ST算法，二者预处理时间都是O(NlogN)，而且ST算法的单次查询操作是O(1)，看起来比线段树好多了，但二者的区别在于线段树支持在线更新值，而ST算法不支持在线操作。

　　这里也存在一个误区，刚学线段树的时候就以为线段树和树状数组差不多，用来处理RMQ问题和求和问题，但其实线段树的功能远远不止这些，我们要熟练的理解线段这个概念才能更加深层次的理解线段树。

二、线段树的基本内容

　　现在请各位不要带着线段树只是为了解决区间问题的数据结构，事实上，是线段树多用于解决区间问题，并不是线段树只能解决区间问题，首先，我们得先明白几件事情。

　　每个结点存什么，结点下标是什么，如何建树。

　　下面我以一个简单的区间最大值来阐述上面的三个概念。

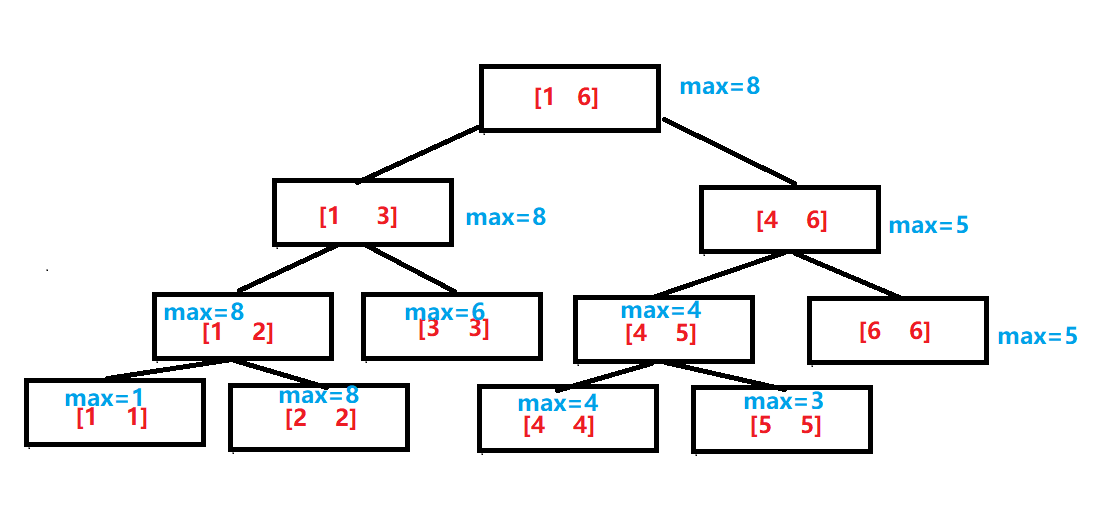
　　对于A[1:6] = {1,8,6,4,3,5}来说，线段树如上所示，红色代表每个结点存储的区间，蓝色代表该区间最值。

　　可以发现，每个叶子结点的值就是数组的值，每个非叶子结点的度都为二，且左右两个孩子分别存储父亲一半的区间。每个父亲的存储的值也就是两个孩子存储的值的最大值。

　　上面的每条结论应该都容易看出来。那么结点到底是如何存储区间的呢，以及如何快速找到非叶子结点的孩子以及非根节点的父亲呢，这里也就是理解线段树的重点以及难点所在，如同树状数组你理解了lowbit就能很快理解树状数组一样，线段树你只要理解了结点与结点之间的关系便能很快理解线段树的基本知识。

　　对于一个区间[l,r]来说，最重要的数据当然就是区间的左右端点l和r，但是大部分的情况我们并不会去存储这两个数值，而是通过递归的传参方式进行传递。这种方式用指针好实现，定义两个左右子树递归即可，但是指针表示过于繁琐，而且不方便各种操作，大部分的线段树都是使用数组进行表示，那这里怎么快速使用下标找到左右子树呢。

　　对于上述线段树，我们增加绿色数字为每个结点的下标

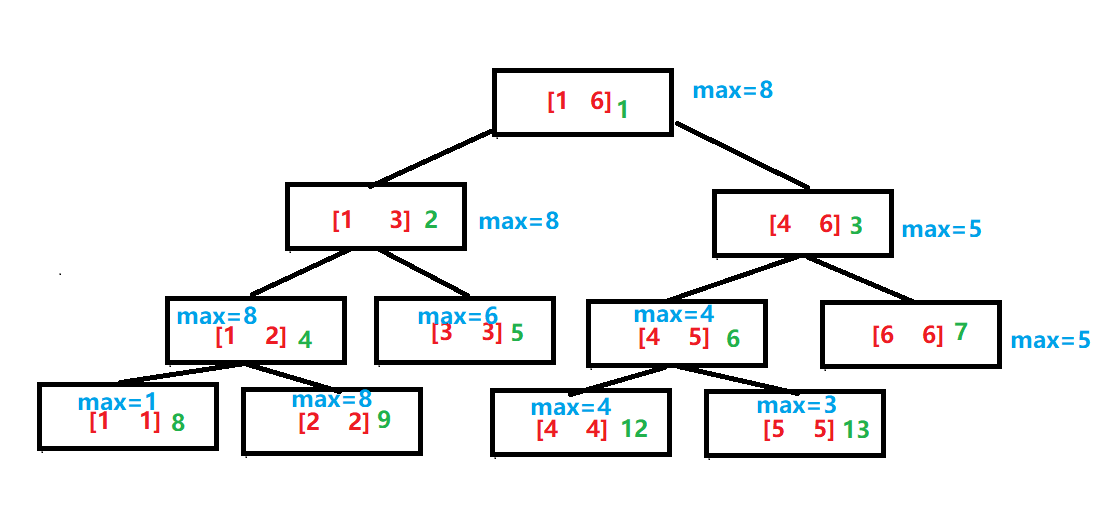
　　则每个结点下标如上所示，这里你可能会问，为什么最下一排的下标直接从9跳到了12，道理也很简单，中间其实是有两个空间的呀！！虽然没有使用，但是他已经开了两个空间，这也是为什么无优化的线段树建树需要2*2^k（2^k-1 < n < 2^k)空间，一般会开到4*n的空间防止RE。

　　仔细观察每个父亲和孩子下标的关系，有发现什么联系吗？不难发现，每个左子树的下标都是偶数，右子树的下标都是奇数且为左子树下标+1，而且不难发现以下规律

• l = fa*2 （左子树下标为父亲下标的两倍）
  
• r = fa*2+1（右子树下标为父亲下标的两倍+1）

　　具体证明也很简单，把线段树看成一个完全二叉树（空结点也当作使用）对于任意一个结点k来说，它所在此二叉树的log2（k） 层，则此层共有2^log2(k)个结点，同样对于k的左子树那层来说有2^log2(k)+1个结点，则结点k和左子树间隔了2*2^log2(k)-k + 2*(k-2^log2(k))个结点，然后这就很简单就得到k+2*2^log2(k)-k + 2*(k-2^log2(k)) = 2*k的关系了吧，右子树也就等于左子树结点+1。

　　是不是觉得其实很简单，而且因为左子树都是偶数，所以我们常用位运算来寻找左右子树

• k<<1（结点k的左子树下标）
  
• k<<1|1（结点k的右子树下标）

 　　整理一下思绪，现在已经明白了数组如何存在线段树，结点间的关系，以及使用递归的方式建立线段树，那么具体如何建立线段树，我们来看代码，代码中不清楚的地方都有详细的注释说明。

 1 const int maxn = 100005;
 2 int a[maxn],t[maxn<<2];        //a为原来区间，t为线段树
 3 
 4 void Pushup(int k){        //更新函数，这里是实现最大值 ，同理可以变成，最小值，区间和等
 5     t[k] = max(t[k<<1],t[k<<1|1]);
 6 }
 7 
 8 //递归方式建树 build(1,1,n);
 9 void build(int k,int l,int r){    //k为当前需要建立的结点，l为当前需要建立区间的左端点，r则为右端点
10     if(l == r)    //左端点等于右端点，即为叶子节点，直接赋值即可
11         t[k] = a[l];
12     else{
13         int m = l + ((r-l)>>1);    //m则为中间点，左儿子的结点区间为[l,m],右儿子的结点区间为[m+1,r]
14         build(k<<1,l,m);    //递归构造左儿子结点
15         build(k<<1|1,m+1,r);    //递归构造右儿子结点
16         Pushup(k);    //更新父节点
17     }
18 }

　　现在再来看代码，是不是觉得清晰很多了，使用递归的方法建立线段树，确实清晰易懂，各位看到这里也请自己试着实现一下递归建树，若是哪里有卡点再来看一下代码找到哪里出了问题。那线段树有没有非递归的方式建树呢，答案是有，但是非递归的建树方式会使得线段树的查询等操作和递归建树方式完全不一样，由简至难，后面我们再说非递归方式的实现。

　　到现在你应该可以建立一颗线段树了，而且知道每个结点存储的区间和值，如果上述操作还不能实现或是有哪里想不明白，建议再翻回去看一看所讲的内容。不要急于看完，理解才更重要。

三、线段树的基本操作

　　基本操作有哪些，你应该也能想出来，在线的二叉搜索树，所拥有的操作当然有，更新和询问两种。

　　1.点更新

　　如何实现点更新，我们先不急看代码，还是对于上面那个线段树，假使我把a[3]+7，则更新后的线段树应该变成

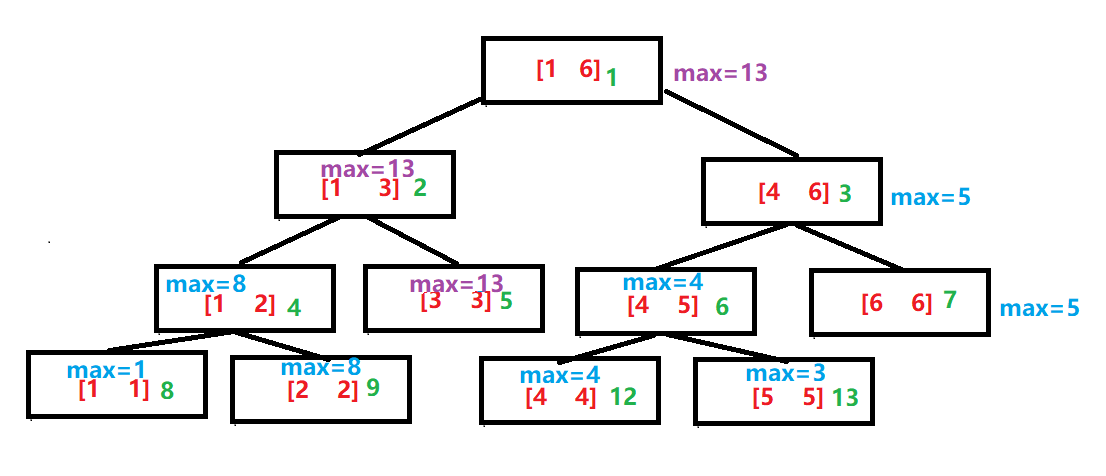
　　更新了a[3]后，则每个包含此值的结点都需要更新，那么有多少个结点需要更新呢？根据二叉树的性质，不难发现是log(k)个结点，这也正是为什么每次更新的时间复杂度为O(logN)，那应该如何实现呢，我们发现，无论你更新哪个叶子节点，最终都是会到根结点的，而把这个往上推的过程逆过来就是从根结点开始，找到左子树还是右子树包含需要更新的叶子节点，往下更新即可，所以我们还是可以使用递归的方法实现线段树的点更新

 1 //递归方式更新 update(p,v,1,n,1);
 2 void update(int p,int v,int l,int r,int k){    //p为下标，v为要加上的值，l，r为结点区间，k为结点下标
 3     if(l == r)    //左端点等于右端点，即为叶子结点，直接加上v即可
 4         a[k] += v,t[k] += v;    //原数组和线段树数组都得到更新
 5     else{
 6         int m = l + ((r-l)>>1);    //m则为中间点，左儿子的结点区间为[l,m],右儿子的结点区间为[m+1,r]
 7         if(p <= m)    //如果需要更新的结点在左子树区间
 8             update(p,v,l,m,k<<1);
 9         else    //如果需要更新的结点在右子树区间
10             update(p,v,m+1,r,k<<1);
11         Pushup(k);    //更新父节点的值
12     }
13 }

　　看完代码是不是很清晰，这里也建议自己再次手动实现一遍理解递归的思路。

　　2.区间查询

　　说完了单点更新肯定就要来说区间查询了，我们知道线段树的每个结点存储的都是一段区间的信息 ，如果我们刚好要查询这个区间，那么则直接返回这个结点的信息即可，比如对于上面线段树，如果我直接查询[1,6]这个区间的最值，那么直接返回根节点信息返回13即可，但是一般我们不会凑巧刚好查询那些区间，比如现在我要查询[2,5]区间的最值，这时候该怎么办呢，我们来看看哪些区间是[2,5]的真子集，

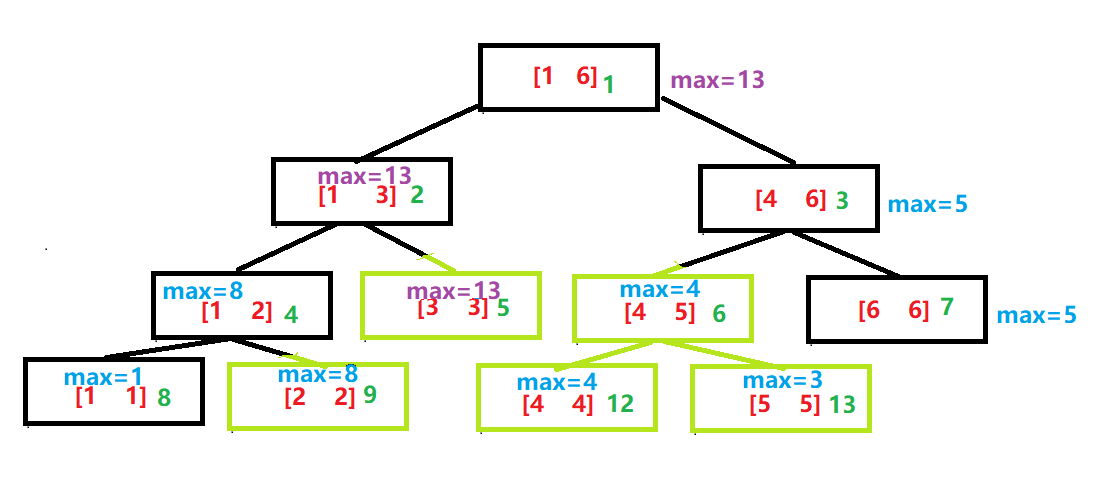
　　一共有5个区间，而且我们可以发现[4,5]这个区间已经包含了两个子树的信息，所以我们需要查询的区间只有三个，分别是[2,2],[3,3],[4,5]，到这里你能通过更新的思路想出来查询的思路吗? 我们还是从根节点开始往下递归，如果当前结点是要查询的区间的真子集，则返回这个结点的信息且不需要再往下递归了，这样从根节点往下递归，时间复杂度也是O(logN)。那么代码则为

 1 //递归方式区间查询 query(L,R,1,n,1);
 2 int query(int L,int R,int l,int r,int k){    //[L,R]即为要查询的区间，l，r为结点区间，k为结点下标
 3     if(L <= l && r <= R)    //如果当前结点的区间真包含于要查询的区间内，则返回结点信息且不需要往下递归
 4         return t[k];
 5     else{
 6         int res = -INF;    //返回值变量，根据具体线段树查询的什么而自定义
 7         int mid = l + ((r-l)>>1);    //m则为中间点，左儿子的结点区间为[l,m],右儿子的结点区间为[m+1,r]
 8         if(L <= m)    //如果左子树和需要查询的区间交集非空
 9             res = max(res, query(L,R,l,m,k<<1));
10         if(R > m)    //如果右子树和需要查询的区间交集非空，注意这里不是else if，因为查询区间可能同时和左右区间都有交集
11             res = max(res, query(L,R,m+1,r,k<<1|1));
12 
13         return res;    //返回当前结点得到的信息
14     }
15 }

　　如果你能理解建树和更新的过程，那么这里的区间查询也不会太难理解。还是建议再次手动实现。

　　3.区间更新

　　树状数组中的区间更新我们用了差分的思想，而线段树的区间更新相对于树状数组就稍微复杂一点，这里我们引进了一个新东西，Lazy_tag，字面意思就是懒惰标记的意思，实际上它的功能也就是偷懒= =，因为对于一个区间[L,R]来说，我们可能每次都更新区间中的没个值，那样的话更新的复杂度将会是O(NlogN)，这太高了，所以引进了Lazy_tag，这个标记一般用于处理线段树的区间更新。
　　线段树在进行区间更新的时候，为了提高更新的效率，所以每次更新只更新到更新区间完全覆盖线段树结点区间为止，这样就会导致被更新结点的子孙结点的区间得不到需要更新的信息，所以在被更新结点上打上一个标记，称为lazy-tag，等到下次访问这个结点的子结点时再将这个标记传递给子结点，所以也可以叫延迟标记。

　　也就是说递归更新的过程，更新到结点区间为需要更新的区间的真子集不再往下更新，下次若是遇到需要用这下面的结点的信息，再去更新这些结点，所以这样的话使得区间更新的操作和区间查询类似，复杂度为O(logN)。

 1 void Pushdown(int k){    //更新子树的lazy值，这里是RMQ的函数，要实现区间和等则需要修改函数内容
 2     if(lazy[k]){    //如果有lazy标记
 3         lazy[k<<1] += lazy[k];    //更新左子树的lazy值
 4         lazy[k<<1|1] += lazy[k];    //更新右子树的lazy值
 5         t[k<<1] += lazy[k];        //左子树的最值加上lazy值
 6         t[k<<1|1] += lazy[k];    //右子树的最值加上lazy值
 7         lazy[k] = 0;    //lazy值归0
 8     }
 9 }
10 
11 //递归更新区间 update(L,R,v,1,n,1);
12 void update(int L,int R,int v,int l,int r,int k){    //[L,R]即为要更新的区间，l，r为结点区间，k为结点下标
13     if(L <= l && r <= R){    //如果当前结点的区间真包含于要更新的区间内
14         lazy[k] += v;    //懒惰标记
15         t[k] += v;    //最大值加上v之后，此区间的最大值也肯定是加v
16     }
17     else{
18         Pushdown(k);    //重难点，查询lazy标记，更新子树
19         int m = l + ((r-l)>>1);
20         if(L <= m)    //如果左子树和需要更新的区间交集非空
21             update(L,R,v,l,m,k<<1);
22         if(m < R)    //如果右子树和需要更新的区间交集非空
23             update(L,R,v,m+1,r,k<<1|1);
24         Pushup(k);    //更新父节点
25     }
26 }

　　注意看Pushdown这个函数，也就是当需要查询某个结点的子树时，需要用到这个函数，函数功能就是更新子树的lazy值，可以理解为平时先把事情放着，等到哪天要检查的时候，就临时再去做，而且做也不是一次性做完，检查哪一部分它就只做这一部分。是不是感受到了什么是Lazy_tag，实至名归= =。

　　值得注意的是，使用了Lazy_tag后，我们再进行区间查询也需要改变。区间查询的代码则变为

 1 //递归方式区间查询 query(L,R,1,n,1);
 2 int query(int L,int R,int l,int r,int k){    //[L,R]即为要查询的区间，l，r为结点区间，k为结点下标
 3     if(L <= l && r <= R)    //如果当前结点的区间真包含于要查询的区间内，则返回结点信息且不需要往下递归
 4         return t[k];
 5     else{
 6         Pushdown(k);    /**每次都需要更新子树的Lazy标记*/
 7         int res = -INF;    //返回值变量，根据具体线段树查询的什么而自定义
 8         int mid = l + ((r-l)>>1);    //m则为中间点，左儿子的结点区间为[l,m],右儿子的结点区间为[m+1,r]
 9         if(L <= m)    //如果左子树和需要查询的区间交集非空
10             res = max(res, query(L,R,l,m,k<<1));
11         if(R > m)    //如果右子树和需要查询的区间交集非空，注意这里不是else if，因为查询区间可能同时和左右区间都有交集
12             res = max(res, query(L,R,m+1,r,k<<1|1));
13 
14         return res;    //返回当前结点得到的信息
15     }
16 }

　　其实变动也不大，就是多了一个临时更新子树的值的过程。

四、线段树的其他操作

　　如果你明白了上述线段树处理区间最值的所有操作，那么转变成求最小值以及区间和问题应该也能很快解决，请手动再实现一下查询区间最小值的线段树和查询区间和的线段树。

　　区间和线段树等代码不再给出，自行实现，若不能实现可以去网上搜索模板对比自己为何不能实现。这里便不再浪费篇幅讲述。

　　这里我便是想说一下线段树还能处理的问题以及一些具体问题讲解。上述我们只是再讲线段树处理裸区间问题，但是大部分问题不会是让你直接更新查询，而是否真正理解线段树便在于思维是否能从区间跳到线段。

　　区间只是一个线段的一小部分，还有一些非区间问题也可以演变成一段一段的线段，然后再通过线段树进行各种操作。下面针对几道例题讲解一下线段树的其他具体用法。

　　下面三道题讲解并非自己所写，而是摘取了另一篇线段树的博客，特此声明，原博客地址：https://blog.csdn.net/whereisherofrom/article/details/78969718

　　1.区间染色

　　给定一个长度为n(n <= 100000)的木板，支持两种操作：
　　1、P a b c       将[a, b]区间段染色成c；
　　2、Q a b         询问[a, b]区间内有多少种颜色；
　　保证染色的颜色数少于30种。
　　对比区间求和，不同点在于区间求和的更新是对区间和进行累加；而这类染色问题则是对区间的值进行替换（或者叫覆盖），有一个比较特殊的条件是颜色数目小于30。
　　我们是不是要将30种颜色的有无与否都存在线段树的结点上呢？答案是肯定的，但是这样一来每个结点都要存储30个bool值，空间太浪费，而且在计算合并操作的时候有一步30个元素的遍历，大大降低效率。然而30个bool值正好可以压缩在一个int32中，利用二进制压缩可以用一个32位的整型完美的存储30种颜色的有无情况。
　　因为任何一个整数都可以分解成二进制整数，二进制整数的每一位要么是0，要么是1。二进制整数的第i位是1表示存在第i种颜色；反之不存在。
　　数据域需要存一个颜色种类的位或和colorBit，一个颜色的lazy标记表示这个结点被完全染成了lazy，基本操作的几个函数和区间求和非常像，这里就不出示代码了。
　　和区间求和不同的是回溯统计的时候，对于两个子结点的数据域不再是加和，而是位或和。

　　2.区间第K大

　　给定n个数，每次询问问[l,r]区间内的第K大数，这个问题有很多方法，但是用线段树应该如何解决呢。

　　利用了线段树划分区间的思想，线段树的每个结点存的不只是区间端点，而是这个区间内所有的数，并且是按照递增顺序有序排列的，建树过程是一个归并排序的过程，从叶子结点自底向上进行归并，对于一个长度为6的数组[4, 3, 2, 1, 5, 6]，建立线段树如图所示。

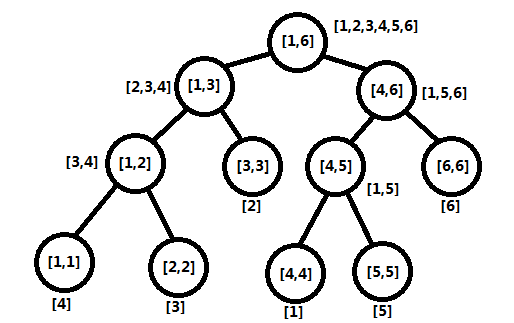
　　从图中可以看出，线段树的任何一个结点存储了对应区间的数，并且进行有序排列，所以根结点存储的一定是一个长度为数组总长的有序数组，叶子结点存储的递增序列为原数组元素。
　　每次询问，我们将给定区间拆分成一个个线段树上的子区间，然后二分枚举答案T，再利用二分查找统计这些子区间中大于等于T的数的个数，从而确定T是否是第K大的。
　　对于区间K大数的问题，还有很多数据结构都能解决，这里仅作简单介绍。

　　3.矩阵面积并

　　对于给定的n(n<=100000)个平行于XY轴的矩形，求他们的面积并。

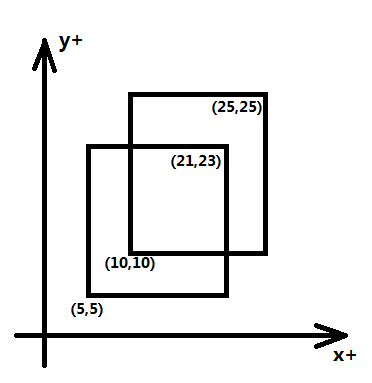
　　这是一个二维的问题，如果我告诉你这道题使用线段树解决，你该如何入手呢，首先线段树是一维的，所以我们需要化二维为一维，所以我们可以使用x的坐标或者y的坐标建立线段树，另一坐标用来进行枚举操作。

　　我们用x的坐标来建树的化，那么我们把矩阵平行于x轴的线段舍去，则变成了

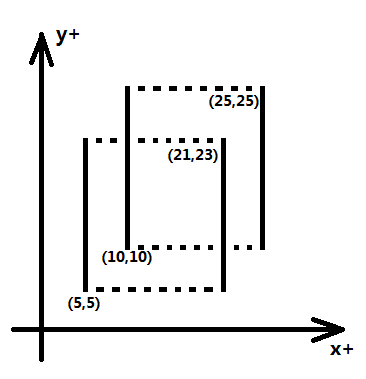
　　每个矩形都剩下两条边，定义x坐标较小的为入边（值为+1），较大为出边（值为-1），然后用x的升序，记第i条线段的x坐标即为X[i]

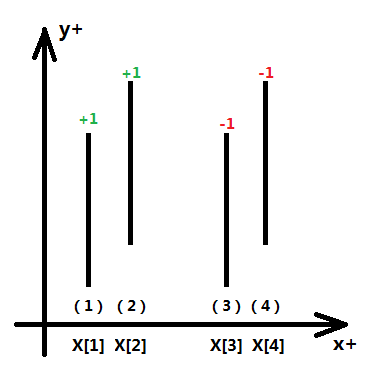
　　接下来将所有矩形端点的y坐标进行重映射(也可以叫离散化)，原因是坐标有可能很大而且不一定是整数，将原坐标映射成小范围的整数可以作为数组下标，更方便计算，映射可以将所有y坐标进行排序去重，然后二分查找确定映射后的值，离散化的具体步骤下文会详细讲解。如图所示，蓝色数字表示的是离散后的坐标，即1、2、3、4分别对应原先的5、10、23、25（需支持正查和反查）。假设离散后的y方向的坐标个数为m，则y方向被分割成m-1个独立单元，下文称这些独立单元为“单位线段”，分别记为<1-2>、<2-3>、<3-4>。

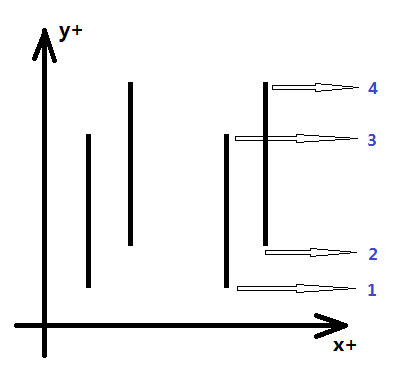
　　以x坐标递增的方式枚举每条垂直线段，y方向用一个长度为m-1的数组来维护“单位线段”的权值，如图所示，展示了每条线段按x递增方式插入之后每个“单位线段”的权值。
　　当枚举到第i条线段时，检查所有“单位线段”的权值，所有权值大于零的“单位线段”的实际长度之和(离散化前的长度)被称为“合法长度”，记为L，那么(X[i] - X[i-1]) * L，就是第i条线段和第i-1条线段之间的矩形面积和，计算完第i条垂直线段后将它插入，所谓"插入"就是利用该线段的权值更新该线段对应的“单位线段”的权值和（这里的更新就是累加）。

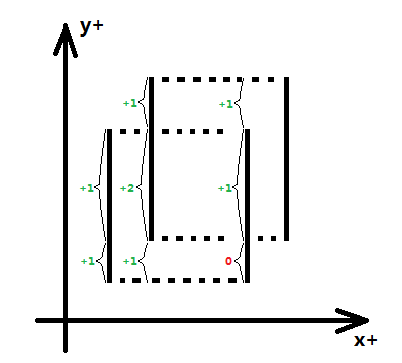
　　如图四-4-6所示：红色、黄色、蓝色三个矩形分别是3对相邻线段间的矩形面积和，其中红色部分的y方向由<1-2>、<2-3>两个“单位线段”组成，黄色部分的y方向由<1-2>、<2-3>、<3-4>三个“单位线段”组成，蓝色部分的y方向由<2-3>、<3-4>两个“单位线段”组成。特殊的，在计算蓝色部分的时候，<1-2>部分的权值由于第3条线段的插入(第3条线段权值为-1)而变为零，所以不能计入“合法长度”。
　　以上所有相邻线段之间的面积和就是最后要求的矩形面积并。

　　优化自然就是用线段树了，之前提到了降维的思想，x方向我们继续采用枚举，而y方向的“单位线段”则可以采用线段树来维护，

　　然后通过一个扫描线来求扫描线覆盖的y的长度。线段的扫描按照x的大小从小到大扫描，求出当前扫描线覆盖的矩阵竖线的长度，然后乘以下条线段的跨度，则为这个区域矩阵覆盖的面积，具体关于扫描线的操作这里不再阐述。这里只讲明白如何建树。

五、线段树的一些重难点以及技巧

　　1.离散化

　　离散化常用于二维状态在一维线段树建树，所谓离散化就是将无限的个体映射到有限个体中，提高算法效率，而且支持正查和反查（从开始遍历和从末尾遍历），可用Hash等实现。

　　2.Lazy_tag

　　这个标记就是用于线段树的区间更新，上面已经提到，便不再累赘，但是区间更新并不局限于使用Lazy_tag，还有一种不使用Lazy_tag的区间更新方法，会在提高篇中讲到。

　　3.空间优化

　　父节点k，左儿子k<<1，右儿子k<<1|1，则需要n<<2的空间，但我们知道并不是所有的叶子节点都占用到了2*n+1 —— 4*n的范围，造成了大量空间浪费。这时候就要考虑离散化，压缩空间。或者使用dfs序作为结点下标，父亲k，左儿子k+1，右儿子k+左儿子区间长度*2，具体实现不再累赘，可自行通过修改左右儿子的下标推出。

　　4.多维推广

　　例如矩阵树，空间树，这些便是线段树的拓展，比如要在两种不同的参数找到最适变量，例如对于一个人的身高和体重，找到一定范围内且年龄最小的人，就可以用到多维推广了。

　　5.可持久化

　　主席树。以后讲= =

　　6.非递归形式

　　前面提到过这个概念，非递归形式的某些操作会快于递归形式，以后将会专门将非递归形式。

　　7.子树收缩

　　就是子树继承的逆过程，继承是为了得到父节点信息，而收缩则是在回溯时候，如果两棵子树拥有相同数据的时候在将数据传递给父结点，子树的数据清空，这样下次在访问的时候就可以减少访问的结点数。

六、相关例题

• codevs 1080 （单点修改+区间查询）
• codevs 1081 （区间修改+单点查询）
• codevs 1082 （区间修改+区间查询）
• codevs 3981 （区间最大子段和）
• Bzoj 3813　  （区间内某个值是否出现过）
• Luogu P2894 （区间连续一段空的长度）
• codevs 2000 （区间最长上升子序列）
• codevs 3044 （矩阵面积求并）
• Hdu 1698 （区间染色+单次统计）
• Poj 2777 （区间染色+批量统计）
• Hdu 4419 （多色矩形面积并）
• Poj 2761 （区间第K大）
• Hdu 2305 （最值维护）

　　暂时只写了这么多，这算是基本的线段树内容，主要就是要明白建树以及各种操作的过程，并且做题时候想这道题是否可以化成线段树建树来解决。

最后

以上就是斯文蜜粉为你收集整理的线段树详解一、什么是线段树？二、线段树的基本内容三、线段树的基本操作四、线段树的其他操作五、线段树的一些重难点以及技巧六、相关例题的全部内容，希望文章能够帮你解决线段树详解一、什么是线段树？二、线段树的基本内容三、线段树的基本操作四、线段树的其他操作五、线段树的一些重难点以及技巧六、相关例题所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。