数据结构进阶——线段树理论概念题目中的Show Time

 

感觉我整理数据结构的速度永远跟不上考试的速度啊…

那么！撰写日期是在7.17，在这一天的模拟赛的T2用到了线段树。虽然打出来了板子但是忘掉了一些东西。

就趁着这个机会AK线段树吧！！

----补于8.6

因为知识体系的庞大，所以这篇博文里包含了朴素线段树、Lazy标记、区间修改、扫描线、动态开点与线段树合并。

但动态开点于线段树合并由于彻底抛弃了某些常用概念。

理论概念

线段树是基于分治思想的二叉树结构。树上的每一个节点都代表一个区间，其根节点就是整个统计范围（1-N），每一个叶节点就是长度为1的区间（也就是一个元素）。对于每个内部节点[l-r]，它的左节点是[l,mid]，右节点是[mid+1,r]，其中mid=(l+r)/2（向下取整）。

根据这些定义，我们大概也能判断他常用的题型了。什么区间最值啊之类的涉及区间的东西。因为他大多情况下是一颗比较完整的完全二叉树（我的意思是不会浪费特别大的空间…），所以我们一般用“父子二倍”的编号方法。即根节点编号为1。对于任意一个节点x，它的左节点为2x，右节点为2x+1。为了保证不会越界，对于N个叶节点的线段树，我们将数组的长度开到4N

搭建

线段树的基本用途就是对序列的维护，支持查询与修改指令。线段树可以非常方便的从下向上传递信息。我们举个区间最小值的例子（诶嘿就是要跟小蓝书反着走！），对于一个节点Data(l,r)，显然Data(l,r)=min(Data(l,mid),Data(mid+1,r))。所以啊，我们用一个结构体保存每个节点。每个节点就包括三个信息。区间左端点L，区间右端点R，和这个节点存放的值Data

那么接下来上一手区间最小值的代码233

struct S{
    int l,r;
    int dat;
}T[4*MAXN];
void build(int p,int l,int r){
    T[p].l=l;//别问我P是什么东西，你用数组的时候总要有个下标的吧= = 
    T[p].r=r;
    if(l==r){//叶子节点！！ 
        T[p].dat=R[l];
        return;
    }
    int mid=(T[p].l+T[p].r)/2;
    build(p*2,l,mid);//左节点 
    build(p*2+1,mid+1,r);//右节点 
    T[p].dat=min(T[p*2].dat,T[p*2+1].dat);//如果你想改成区间最大值，就把这个min函数改动一下好了。 
}

build(1,1,n);//入口 

单点修改

这里支持的修改是单点，也就是一次只更改一个节点的值。你可以指定他改成某个元素或者令他进行计算以改变值。

在线段树中，根节点是各种指令的入口。我们需要从根节点出发，层层递归来找代表着所需区间的节点。然后从下往上更新。

下面上的是复杂度为O(log N)的单点修改

void change(int p,int x,int v){
//v是要减小的值，p是入口，x是所需更该节点的位置
    if(T[p].l==T[p].r){
        T[p].dat-=v;
        return;
    }
    int mid=(T[p].l+T[p].r)/2;
    if(x<=mid){
        change(p*2,x,v);
    }
    else{
        change(p*2+1,x,v);
    }
    T[p].dat=min(T[p*2].dat,T[p*2+1].dat);
}
change(1,x,v);//入口

区间修改

注意：为了把功能放在一起，所以我把这个知识点放在了单点修改下面。但这个知识点更接近于压轴难度。所以可以先看下面的查询功能，再来看这个区间修改。

 

（小声）怎么办小蓝书上并没有纯粹的区间修改…给了个例题还加持了数论的buff

啊数论啊！我数学蒟蒻啊兄Dei！！

好的我们换一个质朴的例题来打板子吧。

 （说着他翻开了小蓝书的下一页，并发现了藏在延迟标记里的区间修改）

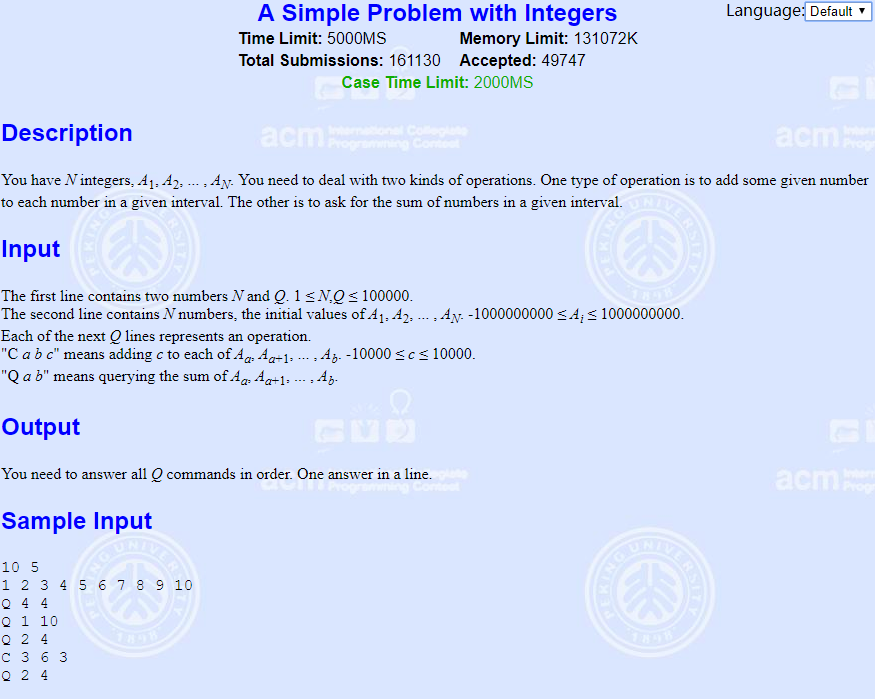
 如果我们要修改区间，那么想想看，如何实现？

众所周知，OI的本质就是倒水（雾）。我们最轻松可以想到的是，直接循环调用单点修改。

那么我们本来高效的O(log N)就这么变成了O(N)！！！！这不能忍。可怎么想，这也没什么可优化的余地啊。那怎么办？

偷懒啊！

什么意思？我们仔细思考一下，这就和我们做作业是一个道理。最恐怖的不是你没做作业，最恐怖的是你废了一大堆时间做作业，老！师！不！检！查！(大雾！！！）

所以，我们就在他每次要求我们修改的时候，只要他不问，我就不修改！

那我怎么要在他问的时候还能让程序记着这个点要修改了再用呢？

这就是延迟标记（也有人叫懒惰/Lazy标记）的作用咯。

那也就是说，我们要在执行修改指令时，发现P点所在区间被完全覆盖时，可以立即返回，不过我们要留一个延迟标记再走。

在后续的指令中，往下递归的时候，如果发现了这里存在一个延迟标记，那么就根据这个标记的内容来更新下方的节点，同时清除这个标记，为下方的子节点打上标记。

故，这个标记的真正定义是：

这个节点曾经被修改，但其子节点尚未被更新。

请留意这个概念，因为犯错概率有点大…

下面放出代码，有些长。

#include<iostream>
using namespace std;
const int MAXN=100010;
struct SegmentTree{
    int l,r;
    long long sum,add;//这个add就是所谓的延迟标记！
     
}tree[MAXN*4];
int a[MAXN],n,m;
void build(int p,int l,int r){
    tree[p].l=l;
    tree[p].r=r;
　　 tree[p].add=0;
    if(l==r){
        tree[p].sum=a[l];
        return ;
    }
    int mid=(l+r)/2;
    build(p*2,l,mid);
    build(p*2+1,mid+1,r);
    tree[p].sum=tree[p*2].sum+tree[p*2+1].sum;
}
void spread(int p){
    if(tree[p].add){
        //如果这个节点被标记了延迟标记
/*
----------Warning--------
延迟标记的意义，是“这个节点曾经被修改，但其子节点尚未被更新。”也就是说，他自己已经更新过了
但他下面的子节点都没有更新。这就意味着我们遇到这个标记的时候，要对他的子节点进行更新。 
*/         
        tree[p*2].sum+=tree[p].add*(tree[p*2].r-tree[p*2].l+1);//更新左节点 
        tree[p*2+1].sum+=tree[p].add*(tree[p*2+1].r-tree[p*2+1].l+1);//更新右节点 
        tree[p*2].add+=tree[p].add;//给左节点打标 
        tree[p*2+1].add+=tree[p].add;//给右节点打标 
        tree[p].add=0;//清除p的标记
         
    }
}
void change(int p,int l,int r,int d){
    if(l<=tree[p].l&&r>=tree[p].r){
        tree[p].sum+=(long long)d*(tree[p].r-tree[p].l+1);//更新该节点 
        tree[p].add+=d;//打上延迟标记 
        return ;
    }
    spread(p);//传播延迟标记
    int mid=(tree[p].l+tree[p].r)/2;
    if(l<=mid){
        change(p*2,l,r,d);
    } 
    if(l>mid){
        change(p*2+1,l,r,d);
    }
    tree[p].sum=tree[p*2].sum+tree[p*2+1].sum;
}
long long ask(int p,int l,int r){
    if(l<=tree[p].l&&r>=tree[p].r){
        return tree[p].sum;
    }
    spread(p);
    int mid=(tree[p].l+tree[p].r)/2;
    long long val=0;
    if(l<=mid){
        val+=ask(p*2,l,r);
    }
    if(r>mid){
        val+=ask(p*2+1,l,r);
    }
    return val;
} 
int main(){
    cin>>n>>m;
    for(int i=1;i<=n;i++){
        cin>>a[i];
    }
    build(1,1,n);
    while(m--){
        char op[2];int l,r,d;
        cin>>op>>l>>r;
        if(op[0]=='C'){
            cin>>d;
            change(1,l,r,d);
        }
        else{
            cout<<ask(1,l,r)<<endl;
        }
    }
}

 

区间查询

想查询某个区间的最值等等？就在这个功能里实现啦！

我们只需要从根节点开始，递归执行这样的操作：

//注：下面的l,r代表的是你需要查询的区间左端点、右端点。

1.若[l,r]完全覆盖了当前节点代表的区间，那么立即回溯，并将该节点的Data值作为候选答案

2.若左子节点和[l,r]有重叠部分，则递归访问左子节点

3.若右子节点与[l,r]有重叠，则递归访问右子节点

那么附上查询的代码

int ask(int p,int l,int r){
    if(l<=T[p].l&&r>=T[p].r){
        return T[p].dat;
    }
    int mid=(T[p].l+T[p].r)/2;
    int val=1<<30;//如果你要查询区间最大值，那么把这个值加个负号就好了。
    if(l<=mid){
        val=min(val,ask(p*2,l,r));
    }
    if(r>mid){
        val=min(val,ask(p*2+1,l,r));
        
    }
    return val;
}

合并

这个操作是在动态开点的线段树上进行的。

什么是动态开点？详见下文在对 A simple Problem with Integers 中的题解。

如果若干个线段树，他们都维护相同的区间[1,n]，那么它们对于各个子区间的划分是一致的。假设有m次单点修改的操作，每次在某一棵线段树上进行。所有操作完成，我们要把对应位置上的值想加，同时得到区间最大值。

对于这个问题，我们就可以用线段树合并来实现。我们依次合并这些线段树。在合并时，用两个指针p,q从两个根节点出发，以递归的方式同步遍历两棵树。确保他们总是代表相同的子区间。

1.若两者有一为空，则以非空者为合并后节点

2.若均不为空，则递归合并两颗左子树和右子树，然后删除q，以p为合并后的节点。自底部向上更新最值信息。

3.如果到达叶子节点，则直接把两个的最值相加

时间复杂度大约在O（m log n）

代码实现如下：

int merge(int p,int q,int l ,int r){
    if(!p){
        return q;
    }
    if(!q){
        return p;
    }
    //如果有任意一边树为空，你不用进行合并
    if(l==r){
        //到达叶子
        tr[p].dat+=tr[q].dat;
        return p; 
    }
    int mid=(l+r)>>1;
    tr[p].lc=merge(tr[p].lc,tr[q].lc,l,mid);//递归合并左子树 
    tr[q].rc=merge(tr[p].rc,tr[q].lc,mid+1,r);//递归合并右子树 
    tr[p].dat=max(tr[tr[p].lc].dat,tr[tr[p].rc].dat);//更新 
    return p;//以p为合并后的节点，相当于删除了q 
} 

 

题目中的Show Time

子题型—扫描线

-------补充于8月6日。不得不说线段树这个知识点是真的庞大…

什么是扫描线？既然是题型，那么就在题目里诠释掉吧。

Atlantis POJ1151

题来

翻译的事情我就不去管了。相信各位都是英文鬼才，精通21国语言那种。

那说一下题目大意，给你N个矩形，矩形可能有重叠。求他们的面积并（也就是重叠部分只算一次）。

第一个数据给测试样例的个数…第二个数据给你个数，下面的数据给你他的顶点坐标………（这是为知识点服务的例题，所以我拒绝花大量功夫在诠释题意上）

那么扫描线是针对这种题型的经典做法。设想有一根线，从下向上抑或从左向右扫过去。那么只有两条矩形临界边会对覆盖面积的大小产生影响。

也就是说，我们从左向右（这里仅以从左向右举例）扫过去，记录下每个矩形的左边和右边。那么他在直线上留下的高度一定是固定的，假定为L。那么其面积一定为L*该段的宽度。

那么这条直线就是扫描线。我们需要取出N个矩形的左右边界，也就是有2N段边线，划分出了2N-1个区间。

我们可以把两个对角顶点坐标暂记为(x1,y1) (x2,y2)并假定x1<x2 , y1<y2

那么就将左边界标记为四元组(x1,y1,y2,1)

右边界标记为(x2,y1,y2,-1)

然后将这2N个四元组间按x进行排序。

但在本题中，y的数据范围不仅很大，而且甚至连整数都不是，所以我们不妨做一下离散化。这里用到一个离散化利器。为了让博文井然有序，我们选择引个超链。

利用sort unique 和Map可以简单的实现离散化。这里设raw(i)表示不同的y值

开一个数组c[i]来表示第i个区间的覆盖次数。c[i]的初始值为0

扫描一遍四元组。对于每一个四元组，我们将其raw(y1)到raw(y2)区间的每个raw[i]加上第四元值（1或者-1），表示覆盖或者结束覆盖。

既然我们要求面积，那如何求呢？长度乘以宽度。宽度一定为x2-x1，那么长度（即在扫描线的高度）是什么呢？

只要c[i]数组不为0，就意味着第i段依然有覆盖。那么局部覆盖长度就是固定的raw(i+1)-raw(i)。我们将长度累加，就可以得到这一条线上被覆盖的总长度。

由此我们得到了长度和宽度，相乘便可以得到局部面积。我们将由此计算来的所有局部面积累加，就得到了最终的面积。

如下是朴素方法的代码实现，其复杂度在O（N²）

#include<iostream>
#include<map>
#include<algorithm>
using namespace std;
const int MAXN=150;
int n,cnt;
double x[MAXN*2],y[MAXN*2];
int c[MAXN*2];
map<double,int> val;
struct Line{
    double x1,y1,y2;
    int p;
}Lines[MAXN*2];
bool Ruler(const Line &a,const Line &b){
    return a.x1<b.x1;
}
double solve(){
    sort(y+1,y+1+2*n);//使用STL中函数的离散化时，必须先进行排序操作
    sort(Lines+1,Lines+1+2*n,Ruler);//为了从左到右依次处理扫描线，我们需要将Lines进行排序
    int y_count=unique(y+1,y+1+2*n)-y-1;//unique完成去重，并且返回去重后数组长度
    for(int i=1;i<=y_count;i++){
        val[y[i]]=i;
        //使用Map实现简单的离散化对应 
    }  
    double ans=0;
    for(int i=1;i<=2*n;i++){
        double y1=Lines[i].y1,y2=Lines[i].y2;
        for(int j=val[y1];j<val[y2];j++){
            c[j]+=Lines[i].p;
        }
        double len=0;
        for(int j=1;j<y_count;j++){
            if(c[j]){
                len+=y[j+1]-y[j];
            }
        }
        ans+=(Lines[i+1].x1-Lines[i].x1)*len;
    } 
    return ans;
}
int main(){
    while(scanf("%d",&n) && n != 0){
        for(int i = 1;i <= n;i++){
            scanf("%lf%lf%lf%lf",&x[i],&y[i],&x[i+n],&y[i+n]);
            //将一个矩形分为两条竖线，存放在lines内
            Lines[i].x1=x[i];
            Lines[i].y1=y[i];
            Lines[i].y2=y[i+n];
            Lines[i].p=1;
            Lines[i+n].x1=x[i+n];
            Lines[i+n].y1=y[i];
            Lines[i+n].y2=y[i+n];
            Lines[i+n].p=-1;
        }
        double ans = solve();
        printf("%.2fnn",ans);
    }
    return 0;
}

 所以说，这和线段树有什么关系呢？

当然是没关系哒！

将扫描线的覆盖次数统计c[i]、覆盖长度y2-y1查询改成对线段树的区间修改、区间查询操作。

那么就可以将计算扫描线的覆盖长度所付出的代价由O(N)降低为O(logN)

Starts in Your Window/窗口的星星 POJ2482/P1502

题来  题来

耗时一夜…补档于8.14 凌晨2:13…

 这里我只写了一遍LuoGu的，我没仔细看，好像两题差不多。如果有差距，下文是LuoGu版本的解法。

首先抛出算法标签，这是一道扫描线的题。首先这道题，可以抽象成我们在拿一个矩形框架框星星，而每个数据的框架大小是固定的。

由于框架大小的固定，我们可以用任何一个顶点来代表这个矩形。我们假定是右上角这格点。这也就是说，对于每一个星星，能框柱它的矩形的右上角会有一个范围。那么对于每个星星的不同范围，产生重叠的区域会同时框住。也就是说，在所有带权的点中，我们需要找到一个权值和最大的重叠区域。

那么问题就向扫描线抽象了。我们只需要界定这个每个区域的边界，也就是矩形的左右两边界。我们可以依然沿用四元组的思维来表示扫描线。

即四元组 (x,y1,y2,id)  其中，x表示横坐标，y1表示矩形下边高，y2表示矩形上边高，id来判断他是左边界还是右边界。

这里由于题目忽略了边框，所以我们对于每个矩形的左下角看做（x,y），右上角看做(x+w-1,y+h-1)，就可以处理掉边框问题。

那么还是使用Map+sort+unique的离散化（我认为比较简洁，是否高效我不做保证），沿用上文经典扫描线的思路进行处理。

这题绝对接受不了O(N²)，所以我们要引入线段树进行处理。

我们关于Y坐标建立一个线段树，维护区间最大值。初始均为0。我们依次处理每个扫描线，让其进行区间修改，并时刻更新最大值。扫描结束时，得到的最大值就是我们需要的答案。

完成一组测试样例后，切记要进行数据清零，否则会影响后续测试。（我测试了一下，不清零是40分哟）

以下完整代码

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<map>
#include<cstring>
using namespace std;
const int Maxn=10010;
int T;
int n,w,h;
map< double , int > Val;
struct node{
    double x,y1,y2;
    int Id;
    node(){}
    node(double x1,double a1,double a2,int iid){
        x=x1;y1=a1;y2=a2;Id=iid;
    }
}Lines[2002000];
int lazy[4004000];
int Maxer[4004000];
int count_y;
int y[2002000];//离散过后的y 
bool Ruler(const node &a,const node &b){
    if(a.x==b.x){
        return a.Id>b.Id;
    }
    return a.x<b.x;
}
void Down(int p,int l,int r){
    if(lazy[p]==0){
        return ;
    }
    Maxer[p]+=lazy[p];
    if(l!=r){
        lazy[p<<1]+=lazy[p];
        lazy[p<<1|1]+=lazy[p];
    }
    lazy[p]=0;    
}
void Change(int p,int l,int r,int x,int y,int z){
    if(x<=l&&y>=r){
        lazy[p]+=z;
        return;
    }
    int mid=(l+r)>>1;
    if(x<=mid){
        Change(p<<1,l,mid,x,y,z);
    }
    if(y>mid){
        Change(p<<1|1,mid+1,r,x,y,z);
    }
    Down(p<<1,l,mid);
    Down(p<<1|1,mid+1,r);
    Maxer[p]=max(Maxer[p<<1],Maxer[p<<1|1]);
}
int slove(){
    int res=0;
    sort(y+1,y+1+n*2);
    sort(Lines+1,Lines+1+n*2,Ruler);
    count_y=unique(y+1,y+1+2*n)-y-1;
    for(int i=1;i<=count_y;i++){
        Val[y[i]]=i;
    }
    //完成离散化
    //Build(1,1,count_y);
     for(int i=1;i<=2*n;i++){
         int l=Val[Lines[i].y1];
         int r=Val[Lines[i].y2];
         Change(1,1,count_y,l,r,Lines[i].Id);
         res=max(res,Maxer[1]);
     }
     return res;
}
void clean(){
    memset(Maxer,0,sizeof(Maxer));
    memset(lazy,0,sizeof(lazy));
} 
int main(){
    scanf("%d",&T);
    while(T--){
         
        scanf("%d%d%d",&n,&w,&h);
        for(int i=1;i<=n;i++){
            int xi,yi,li;
            scanf("%d%d%d",&xi,&yi,&li);
            Lines[i]=node(xi,yi,yi+h-1,li);//可以容纳此星星的矩形范围的左边界 
            Lines[i+n]=node(xi+w-1,yi,yi+h-1,-li);//右边界 
            y[i]=yi;
            y[i+n]=yi+h-1;
        }
        int ans=slove();
        printf("%dn",ans);
        clean();
    }
}

 

A simple Problem with Integers POJ3468

经典解法被我当例题开了。详见上文区间修改讲解。

但是。他还有可以利用的价值。

线段树变形—动态开点

众所周知，当水平恒定在某一个阶段的时候，空间和时间就可以进行相互转换，达到某种平衡就可以AC！我们称其为AC秘法

为了降低空间复杂度，我们可以去尝试不构造出整棵树结构，而是只在建立之初留下一个根节点，代表整个区间。当需要访问线段树的某个子树即某个子区间的时候，再建立这个子区间的节点。这和lazy标记有异曲同工之妙，他们都是有用时再做的优化思想。采用这种方法的线段树，它抛弃了父子2倍编号规则，改为使用变量记录左右子节点的编号。同时，他不保存每个节点代表的区间，而是在每次递归访问的时候作为参数传递。

对于这种变形知识点，我们就直接上演示代码，以获得更直观的理解。

#include<iostream>
using namespace std;
struct SegmentTree{
    int lc,rc;//左右子节点的编号
    int dat;//区间最大值 
    
}tr[SIZE*2];
int root,tot;
int build(){
    tot++;
    tr[tot].lc=tr[tot].rc=tr[tot].dat=0;
    return tot;
}
void instert(int p,int l,int r,int val,int delta){
    if(l==r){
        tr[p].dat+=delta;
        return ;
    }
    int mid=(l+r)>>1;
    if(val<=mid){
        if(!tr[p].lc){
            tr[p].lc=build();//动态开点 
        }
        insert(tr[p].lc,l,mid,val,delta);
    }
    else{
        if(!tr[p].rc){
            tr[p].rc=build();
        }
        insert(tr[p].rc,mid+1,r,val,delta);
    }
    tr[p].dat=max(tr[tr[p].lc].dat,tr[tr[p].rc].dat);
}
int main(){
    tot=0;
    root=build();
    insert(root,1,n,val,delta);//调用 
} 

借教室 NOIP2012提高组Day2真题

抛个链接

----7.18补档

啊，丢死人了。昨天写了一天的线段树，被来打算顺手改好AC这个题做完美谢幕，结果愣是找了一个晚自习的Bug没改出来。

今天仔细看了看，发觉到了一些问题。

最主要的就是，在建树的时候！不！要！忘！记！把！标！记！赋！值！成！0！

其次就是要搞清楚所求范围和节点范围，因为都是r l，所以是相当容易混乱。

我自己试了一下，下面的代码在LuoGu上跑起来确实会有一个点TLE，但这个代码为了可读性（我觉得是），少做了很多优化。比如说把“/2”的操作更改成位运算，加个快读等等。这都能大幅提高速度，所以理论上来说是不会被卡点的。

#include<iostream>
#include<cstdio>
using namespace std;
const long long MAXN=1000010;
long long n,m;
long long R[MAXN];
long long d[MAXN],s[MAXN],t[MAXN];
struct S{
    long long l,r;
    long long dat;
    long long lazy;
}T[4900010];
void build(long long p,long long l,long long r){
    //cout<<p<<" "<<l<<" "<<r<<endl;
    T[p].l=l;
    T[p].r=r;
    T[p].lazy=0;
    if(l==r){
        T[p].dat=R[l];
        return;
    }
    long long mid=(l+r)/2;
    //cout<<mid<<endl;
    build(p*2,l,mid);
    build(p*2+1,mid+1,r);
    T[p].dat=min(T[p*2].dat,T[p*2+1].dat);
}
void spread(long long x){
    if(T[x].lazy!=0){
        //T[x*2].dat-=T[x].lazy*(T[x*2].r-T[x*2].l+1);
    //    T[x*2+1].dat-=T[x].lazy*(T[x*2+1].r-T[x*2+1].l+1);
        T[x*2].dat-=T[x].lazy;
        T[x*2+1].dat-=T[x].lazy;
        T[x*2].lazy+=T[x].lazy;
        T[x*2+1].lazy+=T[x].lazy;
        T[x].lazy=0;
        
    }
}

long long ask(long long p,long long l,long long r){
    if(l<=T[p].l&&r>=T[p].r){
        //spread(p);
        return T[p].dat;
    }
    spread(p);

    long long mid=(T[p].l+T[p].r)/2;
    long long val=1<<30;
    if(l<=mid){
        val=min(val,ask(p*2,l,r));
    }
    if(r>mid){
        val=min(val,ask(p*2+1,l,r));
        
    }
//    for(long long i=1;i<=n;i++){
//        cout<<T[i].dat<<" ";
//    }
//    cout<<endl;
    return val;
}
//ask 1 l r
void change(long long p,long long l,long long r,long long d){
    if(l<=T[p].l&&r>=T[p].r){
        //T[p].dat-=d*(T[p].r-T[p].l+1);//更新该节点
        //spread(p);
        T[p].dat-=d; 
        T[p].lazy+=d;//打上延迟标记 
        return ;
    }
    spread(p);//传播延迟标记
    long long mid=(T[p].l+T[p].r)/2;
    if(l<=mid){
        change(p*2,l,r,d);
    } 
    if(r>mid){
        change(p*2+1,l,r,d);
    }
    T[p].dat=min(T[p*2].dat,T[p*2+1].dat);
}
//change 1 x, v
int main(){
    //freopen("classroom.in","r",stdin);
    //freopen("classroom.out","w",stdout);
    scanf("%d%d",&n,&m);
    //cin>>n>>m;
    //cout<<n<<m<<endl;
    for(long long i=1;i<=n;i++){
        scanf("%d",&R[i]);
        //cin>>R[i];
    }
    for(long long i=1;i<=m;i++){
        //cin>>d[i]>>s[i]>>t[i];
        scanf("%d%d%d",&d[i],&s[i],&t[i]);
    }
    //感觉上，线段树会很好用
    //维护一个区间最小值。如果在这个区间中最小值小于询问时的所需量，则返回订单编号并输出-1
     build(1,1,n);
     for(long long i=1;i<=m;i++){
         
         //cout<<abc<<endl;
         if(ask(1,s[i],t[i])<d[i]){
             
            //printf("-1 n");
             //printf("%d",i);
             //puts(-1);
             printf("%dn%d",-1,i);
             //cout<<-1<<endl<<i;
             //cout<<-1<<endl<<i;
             return 0;
         }
         else{
             change(1,s[i],t[i],d[i]);
         }
     }
     printf("%d",0);
     //cout<<0;
     return 0;
}

代码是考场写的代码修改得来的，考试的时候没写区间修改，复杂度太高所以死的很惨。现在加上这个区间修改，至少在自己学校的OJ上是AC了的。

疯狂的馒头

Input

第一行四个正整数N，M，p，q

Output

一共输出N行，第i行表示第i个馒头的最终颜色（如果最终颜色是白色就输出0）。

Sample Input

4 3 2 4

Sample Output

2

2

3

0

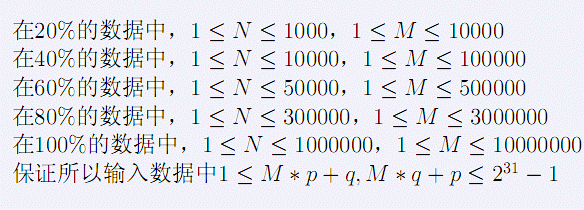
这个题其实也可以用个线段树。十分有趣，要稍微做点变形。把染色的步骤倒过来。这样，只要这个节点已经有颜色了，那么他就不能再次被染色。

#include<iostream>
#include<cstdio>
using namespace std;
const int MAXN=1e7+10;
int n,m,p,q;
int Left;
int Right;
struct chui{
    int l;
    int r;
    int color;
}Tree[MAXN*4];
void Build(int p,int l,int r,int colo,int L,int R){
    if(Tree[p].color){
        return;
    }
    //Tree[p].l=l;
    //Tree[p].r=r;
    if(l==r){
        Tree[p].color=colo;
        //ans[l]=Tree[p].color;
        return;
    }
    int mid=(l+r)/2;
    if(L<=mid){
        Build(p*2,l,mid,colo,L,R);
    }
    if(R>mid){
        Build(p*2+1,mid+1,r,colo,L,R);
    }
    Tree[p].color=Tree[p*2].color&&Tree[p*2+1].color;
}
void Print(int p,int l,int r){
    if(l==r){
        printf("%dn",Tree[p].color);
        //cout<<Tree[p].color<<endl;
        return;
    }
    int mid=(l+r)/2;
    Print(p*2,l,mid);
    Print(p*2+1,mid+1,r);
}
int main(){
    cin>>n>>m>>p>>q;
    
    for(int i=m;i>=1;i--){
        Left=(1ll*i*p+q)%n+1;
        Right=(1ll*i*q+p)%n+1;
        if(Left>Right){
            swap(Left,Right);
        }
        Build(1,1,n,i,Left,Right);
    }
    Print(1,1,n);
} 

 小白逛公园 P4513

题来

这题比较容易看出来是个区间和的最大值问题。一个区间的最大值会如何产生呢？

1.从区间左端点l开始，向右得到

2.从区间又端点r开始，向左得到

3.跨过中间点Mid，从左半边的右端点向左，从右半边的左端点向右得到。

那么，我们就需要维护四个数据：

从左开始得到的最大子段和值

从右开始得到的最大子段和值

整个区间的最大子段和值

整个区间段和

这么一寻思，满足向上传递的性质，自然就会想到线段树来维护这个操作。那么如何来维护这几个个数据呢？

void Update(int p)
{
    int left=p<<1;
    int right=p<<1|1;
    Tree[p].sum=Tree[left].sum+Tree[right].sum;
    Tree[p].lmax=max(Tree[left].lmax,Tree[left].sum+Tree[right].lmax);
    Tree[p].rmax=max(Tree[right].rmax,Tree[right].sum+Tree[left].rmax);
    Tree[p].Max=max(max(Tree[left].Max,Tree[right].Max),Tree[left].rmax+Tree[right].lmax);

}

因为用不着什么下放，故不需要搞Lazy标记

那么完整AC代码：

#include<iostream>
#include<cstdio>
using namespace std;
const int MAXN=500010;
int n,m;
int Read_in[MAXN];
struct node
{
    int sum;
    int lmax;
    int rmax;
    int Max;
    int l;
    int r;
} Tree[MAXN*4];
void Update(int p)
{
    int left=p<<1;
    int right=p<<1|1;
    Tree[p].sum=Tree[left].sum+Tree[right].sum;
    Tree[p].lmax=max(Tree[left].lmax,Tree[left].sum+Tree[right].lmax);
    Tree[p].rmax=max(Tree[right].rmax,Tree[right].sum+Tree[left].rmax);
    Tree[p].Max=max(max(Tree[left].Max,Tree[right].Max),Tree[left].rmax+Tree[right].lmax);

}
void Build(int P,int l,int r)
{
    Tree[P].l=l;
    Tree[P].r=r;
    if(l==r)
    {
        Tree[P].lmax=Tree[P].rmax=Tree[P].Max=Tree[P].sum=Read_in[l];
        return ;
    }
    int mid=(l+r)>>1;
    Build(P<<1,l,mid);
    Build(P<<1|1,mid+1,r);
    Update(P);

}
void change(int p,int pos,int num)
{
    if(Tree[p].l==Tree[p].r)
    {
        Tree[p].sum=Tree[p].lmax=Tree[p].rmax=Tree[p].Max=num;
        return ;
    }
    int mid=(Tree[p].l+Tree[p].r)>>1;
    if(mid>=pos)
    {
        change(p<<1,pos,num);
    }
    else
    {
        change(p<<1|1,pos,num);
    }
    Update(p);
}
node Ask(int p,int l,int r)
{
    if(l<=Tree[p].l&&Tree[p].r<=r)
    {
        return Tree[p];
    }
    int mid=(Tree[p].l+Tree[p].r)>>1;
    if(r<=mid)
    {
        return Ask(p<<1,l,r);
    }
    else if(l>mid)
    {
        return Ask(p<<1|1,l,r);
    }
    else
    {
        node x=Ask(p<<1,l,r);
        node y=Ask(p<<1|1,l,r);
        node re;
        re.sum=x.sum+y.sum;
        re.lmax=max(x.sum+y.lmax,x.lmax);
        re.rmax=max(y.sum+x.rmax,y.rmax);
        re.Max=max(max(x.Max,y.Max),x.rmax+y.lmax);
        return re;
    }
}
int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1; i<=n; i++)
    {
        scanf("%d",&Read_in[i]);
    }
    Build(1,1,n);
    int Index,a,b;
    node ans;
    for(int i=1; i<=m; i++)
    {
        scanf("%d",&Index);
        if(Index==1)
        {
            scanf("%d%d",&a,&b);
            if(a>b)
            {
                swap(a,b);
            }
            ans=Ask(1,a,b);
            printf("%dn",ans.Max);
        }
        else
        {
            scanf("%d%d",&a,&b);
            change(1,a,b);
        }
    }
}