加减运算

原码

• 加法：先判符号位。若相同，则绝对值相加，结果符号位不变。若不同，做减法，绝对值大的减去绝对值小的数，结果符号位与绝对值大的相同。
• 减法：减数符号取反做加法运算。*注意机器字长，当左边位出现溢出时，将溢位丢掉。

补码

1. 参与运算的操作数均用补码表示
   菜鸡笔记：正数补码与原码相同，负数补码取反加1

2. 二进制规则运算，逢二进一

3. 符号位与数值位按同样的规则运算一起参与运算，符号位产生的进位要丢掉，结果的符号位由运算得出

4. 运算公式：[A+B]_补=[A]_补+[B]_补（mod M）
   [A-B]_补=[A]_补+[-B]_补(mod M)
   mod M运算是为了将溢出位丢掉
   *菜鸡笔记：mod运算 求余运算 mod2即模2运算
   模运算的性质：带余除法——设 x,m∈Z，m>0,则存在唯一决定的整数q（商）和r（余数）,使得 x=qm+r,0<=r<m
   19 mod 12 = 7(及19/12=1…7)
   -3 mod 12 = 9 (-3对12取模为9)
   9 mod 12 = 9 （9对12取模为9）
   在模12的条件下，-3等价于9，|-3|+|9|=12
   -3 mod 12 = r
   -3 = (-1) * 12 + 9
   9 mod 12 = r
   9 = 0 * 12 +9 （mod12把整数分为12类余数（0~11），余数相同的为同类等价。）

5. 补码运算结果亦为补码
   【例】设机器字长为8位（含一位符号位），A = 15，B = 24.求[A+B]_补，[A-B]_补。
   解：
   A = +15 = 00001111 B = +24 = 00011000；得[A]_补 = 00001111 [B]_补 = 00011000
   [A + B]_补=[A]_补 + [B]_补=00100111，其符号位为0，对应的真值为+39
   [-B]_补=11101000
   [A - B]_补 = [A]_补 + [-B]_补= 11110111，其符号为1，对应的真值为-9
   注意负数，原码与补码转换：取反加1

符号扩展

在计算机算数运算中，有时必须把采用给定位数表示的数转换成具有不同位数位数的某种表现形式。
int–>long 短数据变为长数据。
e.g. 8位–>16位。正数（原、反、补码的形式都一样）原有形式的符号都移到新形式的符号位上，新表示形式的所有附加位都用0进行填充。

定点整数的符号扩展：在原符号位和数值位中间添加新位，正数都添0；负数原码添0，负数反、补码添1

定点小数的符号扩展：在原符号位和数值位后面添加新位，正数都添0；负数原、补码添0，负数反码添1

溢出判断

key:`正+正=负（上溢）、负+负=正（下溢）

• 一位符号位，参加操作的两个数符号相同，结果又与原操作数符号不同，则表示结果溢出
  菜鸡笔记：AB:与&&、A+B：或||、非 ！
  设A的符号为A_s，B的符号为B_s，运算结果的符号为S_s，则逻辑溢出表达式为：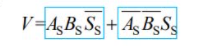
  若V = 0，表示无溢出；若V = 1，表示有溢出。

• 双符号位（模4补码）
  运算结果的两个符号位S_s1S_s2相同，表式未溢出；否则溢出，此时最高位符号代表真正的符号。（实际存储时，只存储一个符号位，运算时会复制一个符号位）
  （1）S_s1S_s2 = 00：表示结果为正数，无溢出
  （2）S_s1S_s2 = 01：表示结果正溢出（上溢）
  （3）S_s1S_s2 = 10：表示结果负溢出（下溢）
  （4）S_s1S_s2 = 11：表式结果为负数，无溢出
  逻辑表达式为：V = S_s ⊕ S₁
  V = 0，无溢出；V = 1，有溢出。
• 采用一位符号位根据数据位的进位情况判断
  若符号的进位C_s与最高位数的进位C₁相同，则说明没有溢出。溢出的逻辑判断表达式为V = C_s ⊕ C₁，若V = 0，无溢出；V=1，有溢出。

`

最后

以上就是伶俐御姐为你收集整理的加减运算&溢出判断加减运算符号扩展溢出判断的全部内容，希望文章能够帮你解决加减运算&溢出判断加减运算符号扩展溢出判断所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。