目录

1. 前言

2. 皮尔逊相关系数定义

3. 数学性质

3.1 对称性

3.2 位移不变性

3.3 尺度不变性

4. 5个假设

5. 几何解释

6. Some calculation examples

Example1: 

Example2: Two random sequence with normal distribution

Example3

1. 前言

        相关是最常用的统计度量。用一个数来描述两个变量之间的相关联的程度。相关系数的取值范围为[-1, +1]。负值表示随着一个变量值的增大另一个则减小；正值表示随着一个变量值的增大另一个也跟着增大；0则表示一个变量的增大减小对另一个的取值没有 影响。

        三种常用的相关系数为：皮尔逊相关系数，斯皮尔曼相关系数，Kendall相关系数.

        本文概要性地介绍皮尔逊相关系数。

       关于斯皮尔曼相关系数的介绍参见斯皮尔曼相关(Spearman correlation)系数概述及其计算例简要介绍了斯皮尔曼相关系数(Spearman correlation coefficient)的概念、计算公式，以及手动计算例、调用scipy函数、pandas函数计算的代码示例。。。https://blog.csdn.net/chenxy_bwave/article/details/121427036        关于Kendall相关系数，参见肯德尔（Kendall）相关系数概述及计算例https://chenxiaoyuan.blog.csdn.net/article/details/126919019

2. 皮尔逊相关系数定义

    最常用的相关就是皮尔逊相关（Pearson correlation）,得名于Karl Pearson, 他从弗朗西斯·高尔顿在19世纪80年代提出的一个相似却又稍有不同的想法演变而来的，这个相关系数也称作“皮尔逊积矩相关系数(Pearson Product-Moment Correlation)”。皮尔逊相关系数通常用字母r表示（所以常常写作 Pearson's r，当然也有用rho来表示），衡量两个随机变量之间的线性关系（或者说线性关联度）。

        两个变量之间的总体(population)的皮尔逊相关系数定义为两个变量之间的协方差和标准差之积的商（或者说，归一化的协方差），通常用rho表示，定义如下：

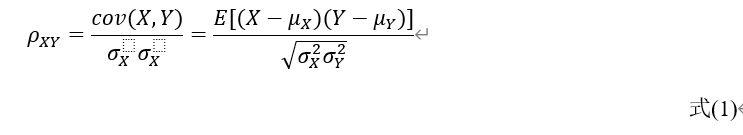
       估算样本的协方差和标准差，可得到(样本的)皮尔逊相关系数，常用英文小写字母 

r 代表，r 的表达式如下所示：

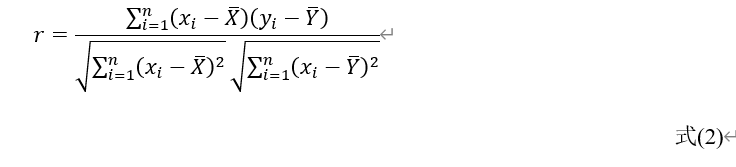
        * 以上分母中后半部分应该是yi而不是xi. 

        其中， 和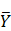 分别表示两者的样本均值。

        R=1表示两者完美的正向线性相关，即满足Y = aX+b(a>0)的关系; R=-1表示两者完美的负向线性相关，即满足Y = aX+b(a<0)的关系. 在X-Y散点图上看的话，散点图完全处于一条直线上。R=0则表示两者没有（线性）相关性。

        以下各图分别以散点图表示的各种线性相关关系示例：

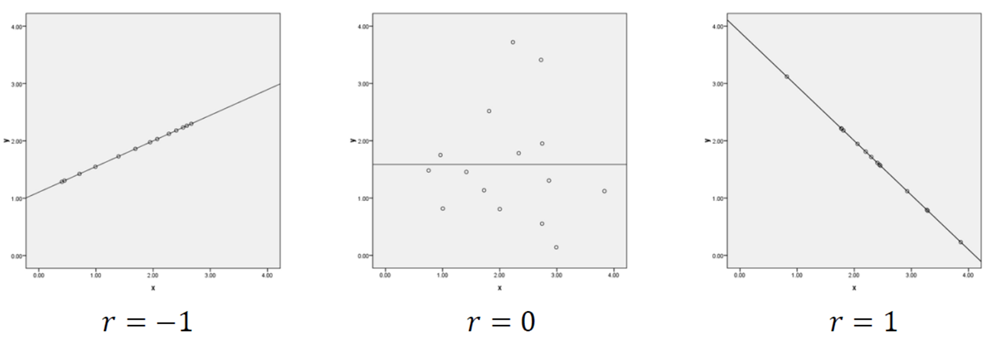
图 1 (左)完全正相关；(中)不相关；（右）完全负相关；（左右两图的r标反了） 

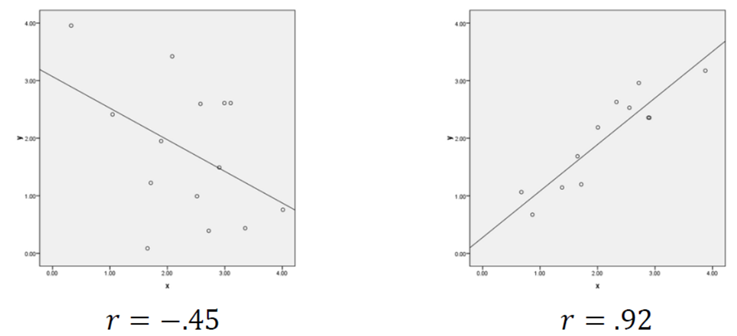
图 2 (左)moderate negative correlation；(右)Strong positive correlation

       需要注意的是，皮尔逊相关系数只是线性关系的度量，如果为0的话，那只是表示两个变量之间没有线性关系，但是它们之间仍然可能存在别的关系！如下图所示： 

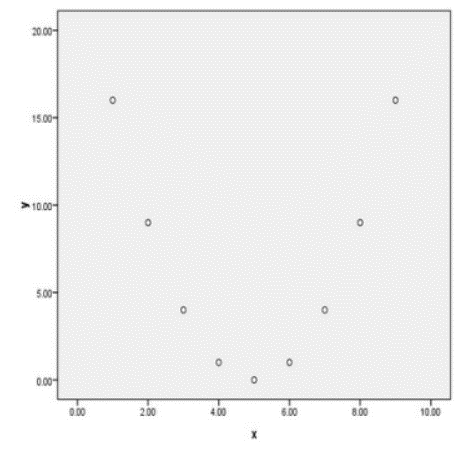
图 3 perfect quadratic relationship

        这个散点图中的x和y之间的皮尔逊相关系数为0，但是仅目测就知道两者之间并不是毫无关系，事实上它们之间存在着完全的平方关系。

        另外一个常见的误解是把相关关系当成了因果关系。。。

        关于（线性）相关的大小（强度），Evans (1996)建议根据r的绝对值进行如下划分:

         .00-.19 “very weak”

         .20-.39 “weak”

         .40-.59 “moderate”

         .60-.79 “strong”

         .80-1.0 “very strong”

        当然，其实这只是一个定义的问题。也有人仅仅将相关关系强度仅仅分为三档[Ref3]，如下所示：

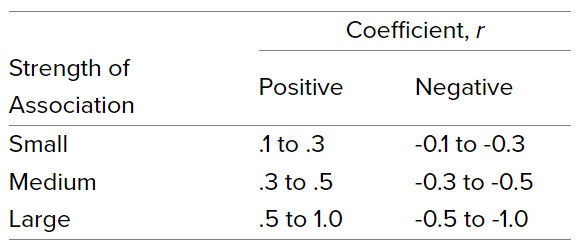
3. 数学性质

3.1 对称性

        由以上皮尔逊系数的表达式可知，皮尔逊系数是对称的。即：

3.2 位移不变性

        直观地看，由于在皮尔逊相关计算（不管是总体的、还是样本的）中，分子（两者的协方差）和分母（各自的方差）都通过减去均值(中心化，或者均值归一化)将均值的影响消除掉了，因此X和Y的均值的变化不会影响两者之间的皮尔逊相关系数。

        具体一点说，令 ，可以得到：

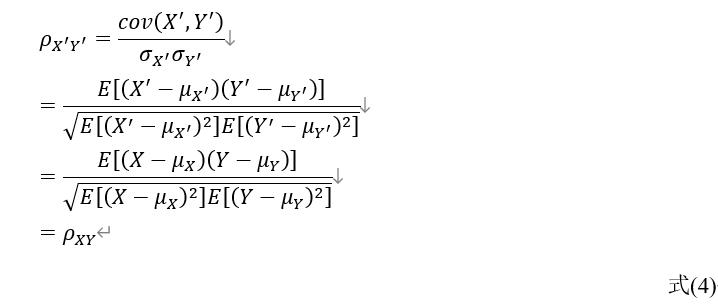
        以上成立的原因在于：

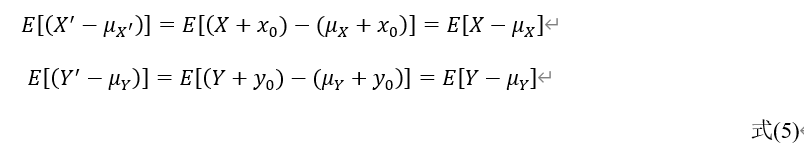
3.3 尺度不变性

        同样，令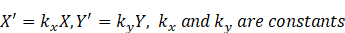 ，可以得到：

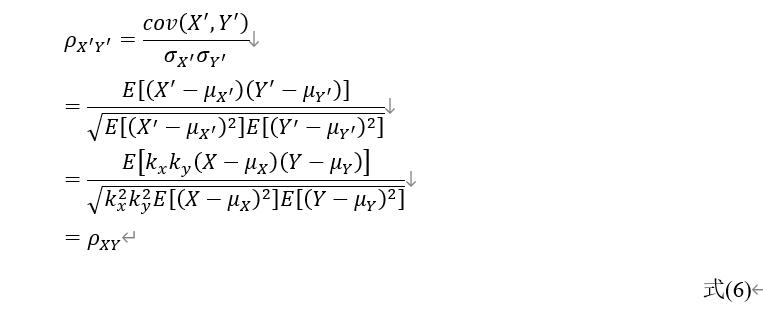
        结合以上两节的结论，可以得到： 

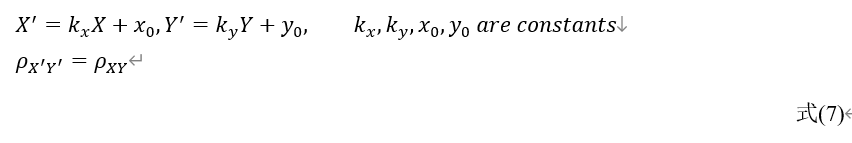
4. 5个假设

        皮尔逊相关性检测要求数据满足一些前提条件，参见[Ref1],[Ref4]:《皮尔逊相关系数的5个假设》。

        另外，[Ref3]中给出了更详细一点的假设方面的描述。

5. 几何解释

        [Ref2]对于没有中心化(或者说均值归一化，mean normalization)的数据, 相关系数与两条可能的回归线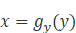 和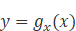 夹角的余弦值一致。

        对于中心化过的数据 (也就是说, 数据移动一个样本平均值以使其均值为0)，相关系数也可以被视作由两个随机变量向量夹角的余弦值。

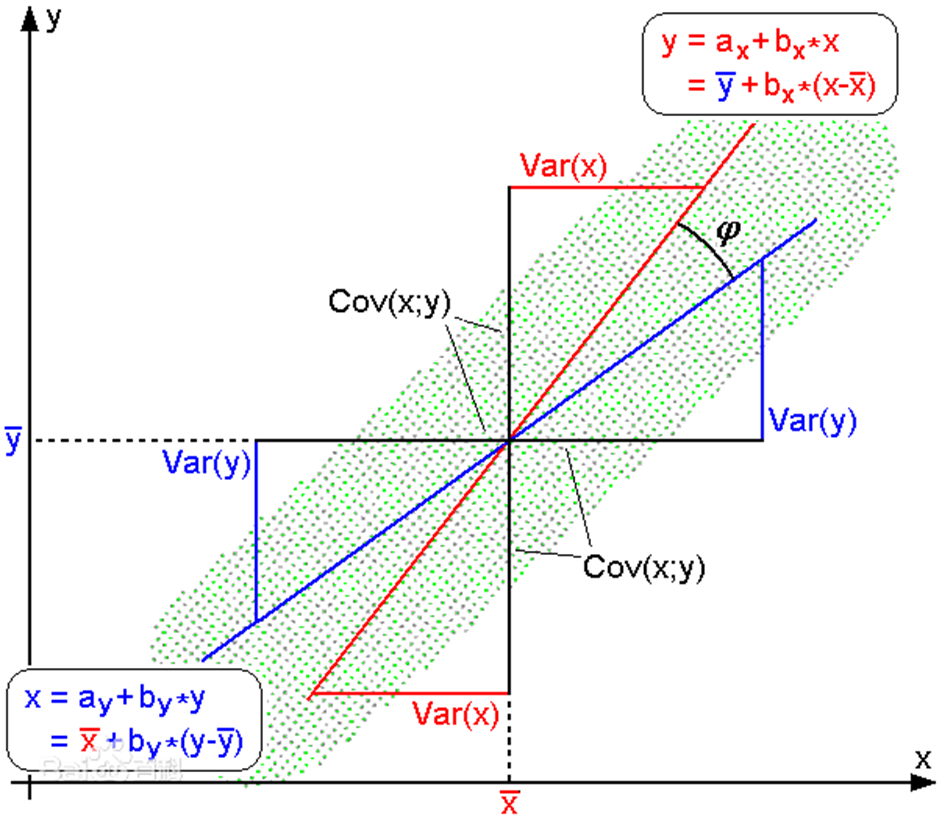
图 4 皮尔逊相关系数几何解释示意图（[Ref2]）

        具体的数学推导可以参考[Ref5]. 

6. Some calculation examples

        本章介绍几个基于scipy.stats.pearsonr()的皮尔逊相关系数计算例（Jupyter Notebook）。

import matplotlib.pyplot as plt
%matplotlib inline
import numpy as np
from scipy import stats

Example1: 

# Example1
dat1 = np.array([3,5,1,6,7,2,8,9,4])
dat2 = np.array([5,3,2,6,8,1,7,9,4])
fig,ax = plt.subplots()
ax.scatter(dat1,dat2)
stats.pearsonr(dat1,dat2)

(0.8999999999999999, 0.0009430623223403325)

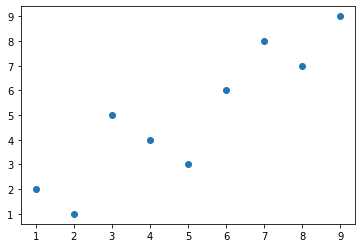
         计算结果表明这两个序列的皮尔逊相关系数高达0.9。stats.pearsonr()除了返回相关系数外，还顺带计算了对应的p-value。直观的理解是，p-value表示两个零相关的序列能够给出这个相关系数的概率，以上p-value为0.0009表明两个零相关的序列的相关系数的绝对值大于等于0.9的概率不足千分之一。从另一个侧面说明了这个相关系数结果的置信度。

Example2: Two random sequence with normal distribution

#Example2: Two random sequence with normal distribution
rng = np.random.default_rng()
x2n = rng.standard_normal((100,))
y2n = rng.standard_normal((100,))
fig, ax = plt.subplots()
ax.scatter(x2n,y2n)
ax.set_xlabel('x2n')
ax.set_ylabel('y2n')
stats.pearsonr(x2n, y2n)

(0.052116156672907456, 0.6065813608252906)

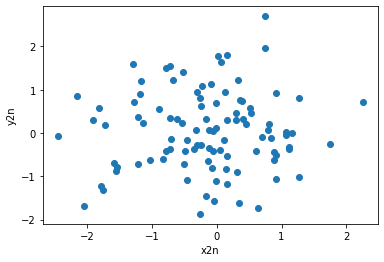
        以上结果中有两个数值，第一个数值为相关系数，第二数值为p值。p值表示的是显著性水平，p值越小表示该结果越具有显著性。直观地理解就是任意两个随机变量序列的相关系数的绝对值大于等于这个值的概率。

        以上结果表明这两个正态随机变量样本序列的相关系数只有0.05，且任意两个随机变量序列的相关系数的绝对值大于等于这个值的概率接近60%，说明这确实是两个不相关的随机变量的样本序列。注意，重复运行以上代码段会得到不同的结果（可能变化比较大，系列越长的话波动就会相应地变小）

Example3

#Example3
rng = np.random.default_rng()
x2n = rng.standard_normal((100,))
y2n = np.array(x2n)**2
fig, ax = plt.subplots()
ax.scatter(x2n,y2n)
ax.set_xlabel('x2n')
ax.set_ylabel('y2n')
stats.pearsonr(x2n, y2n)

(0.00841691124614799, 0.9337621987673613)

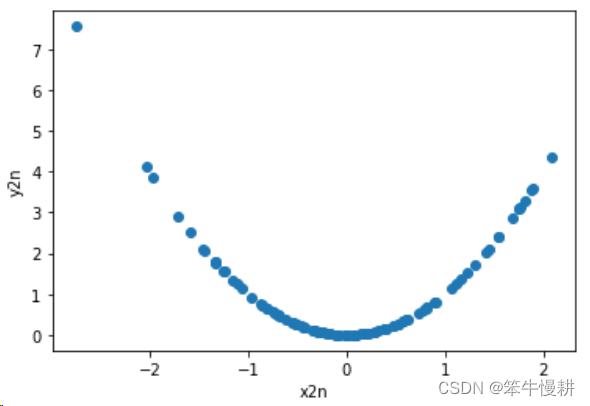
        这个例子给出的两个随机变量的遵循平方关系。可以看出它们之间的皮尔逊相关系数很小，符合预期。事实上符合平方关系的两个随机变量X,Y的总体的相关系数应该为0. 以上因为是采样数据，所以存在一定的偏差。

[Ref1] The Five Assumptions for Pearson Correlation - Statology

[Ref2] 皮尔逊相关系数_百度百科 (baidu.com)

[Ref3] Pearson Product-Moment Correlation - When you should run this test, the range of values the coefficient can take and how to measure strength of association.

[Ref4] 皮尔逊相关系数的5个假设

[Ref5] Zenon Gniazdowski,” Geometric interpretation of a correlation”

[Ref6] 斯皮尔曼相关(Spearman correlation)系数概述及其计算例

最后

以上就是爱撒娇流沙为你收集整理的皮尔逊相关(Pearson correlation)系数概述及其计算例1. 前言2. 皮尔逊相关系数定义3. 数学性质4. 5个假设5. 几何解释6. Some calculation examples的全部内容，希望文章能够帮你解决皮尔逊相关(Pearson correlation)系数概述及其计算例1. 前言2. 皮尔逊相关系数定义3. 数学性质4. 5个假设5. 几何解释6. Some calculation examples所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。