1 理论
计算定积分时,可以通过微元法逼近,如下:
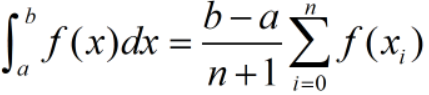
若取值均匀,公式如下:
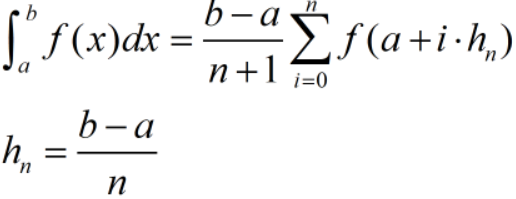
通过上述公式可以看到,定积分的值可以通过取样点函数值的线性组合得到。当取样点已经确定时,定积分的精度取决于每个取样点所分配的权值。梯形公式、Simpson公式、Cotes公式、Romberg公式正是通过调整权值来逐步逼近积分值。
(1)复合梯形公式
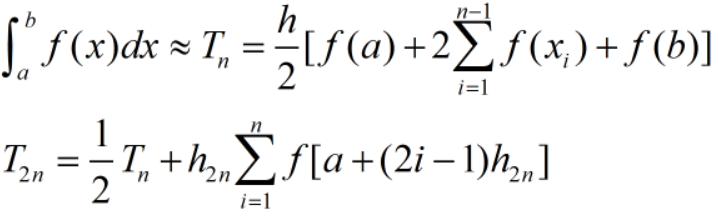
(2) Simpson公式
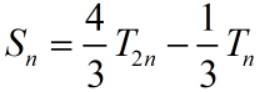
(3)Cotes公式
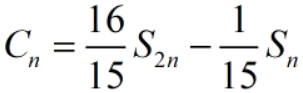
(4)Romberg公式
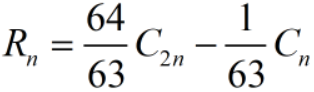
2 实验
借助如下公式,使用 Romberg 求积公式计算
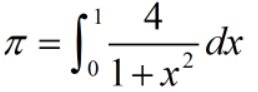
import numpy as np
def fun(x):
return 4/(1+x*x)
def romberg(a,b,m): # m>=3
p=np.zeros(m+1,dtype='int32') #p[i]=2**i
p[0]=1;
for i in range(1,m+1):
p[i]=p[i-1]*2
n=p[m]
d=b-a
f=np.random.uniform(a,b,n+1) #保存函数值
for i in range(n+1):
x=a+d/n*i
f[i]=fun(x)
print("f=n",f)
T=np.random.uniform(a,b,m) #保存梯度值
T[0]=(f[0]+f[n])/2
for i in range(1,m):
s=0.0
for k in np.arange(1,p[i-1]+1):
s+=f[(2*k-1)*p[m-i]]
T[i]=T[i-1]/2+d/p[i]*s
print("T=n",T)
S=np.random.uniform(a,b,m-1)
for i in range(m-1):
S[i]=(4*T[i+1]-T[i])/3 #Simpson公式
print("S=n",S)
C=np.random.uniform(a,b,m-2)
for i in range(m-2):
C[i]=(16*S[i+1]-S[i])/15 #Cotes公式
print("C=n",C)
R=np.random.uniform(a,b,m-3)
for i in range(m-3):
R[i]=(64*C[i+1]-C[i])/63 #Romberg公式
print("R=n",R)
return R[-1]
s=romberg(0,1,8)T=
[3. 3.1 3.13117647 3.13898849 3.14094161 3.14142989
3.14155196 3.14158248]
S=
[3.13333333 3.14156863 3.1415925 3.14159265 3.14159265 3.14159265
3.14159265]
C=
[3.14211765 3.14159409 3.14159266 3.14159265 3.14159265 3.14159265]
R=
[3.14158578 3.14159264 3.14159265 3.14159265 3.14159265]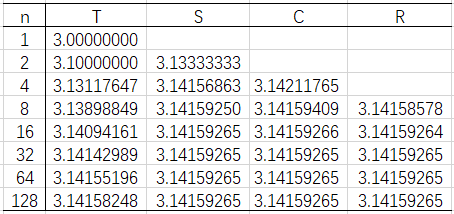
从运行结果可以看出,在取样点相同的情况下,梯形公式、Simpson公式、Cotes公式、Romberg公式的精度依次增加。
最后
以上就是长情小蘑菇最近收集整理的关于数值积分原理与应用的全部内容,更多相关数值积分原理与应用内容请搜索靠谱客的其他文章。
本图文内容来源于网友提供,作为学习参考使用,或来自网络收集整理,版权属于原作者所有。








发表评论 取消回复