笔者(萌新)的两三话:本科是海员专业,研究生转行,无任何基础,总算自认为把自抗扰的原理和各个公式部分搞懂了,希望个人的学习经历可以帮助其他人。 会有大量的转载别人的内容(会标明出处和链接)
TD篇
- 一:所用到的两篇参考论文和相关博客
- 二:DT的基本数学表达式
- 三:对TD数学表达式进行说明和讲解(从零讲起)
- 3.1 TD数学表达式的起源(起源是最速控制综合函数)
- 3.2 最速控制综合函数的推导(本章大量转载别人的博客,请见谅,会标明出处)
- 3.2.1 参考博客和论文
- 3.2.2 最速控制综合函数的物理意义和数学建模
- 本说明的所有变量声明表
- 重点说明部分部分,三种情况的分类说明。
- 3.3 DT的离散形式 韩老先生把最速控制函数改造在自抗扰控制的DT中
- 3.3.1 k≥3的情况
- 3.3.2 k≤2 的情况
- 3.3.3 最终结果
一:所用到的两篇参考论文和相关博客
开源飞控ACFLY:ADRC离散系统最速控制综合函数的理解
韩京清教授的跟踪微分器的离散形式(论文)
离散系统最速控制综合函数(论文)
二:DT的基本数学表达式
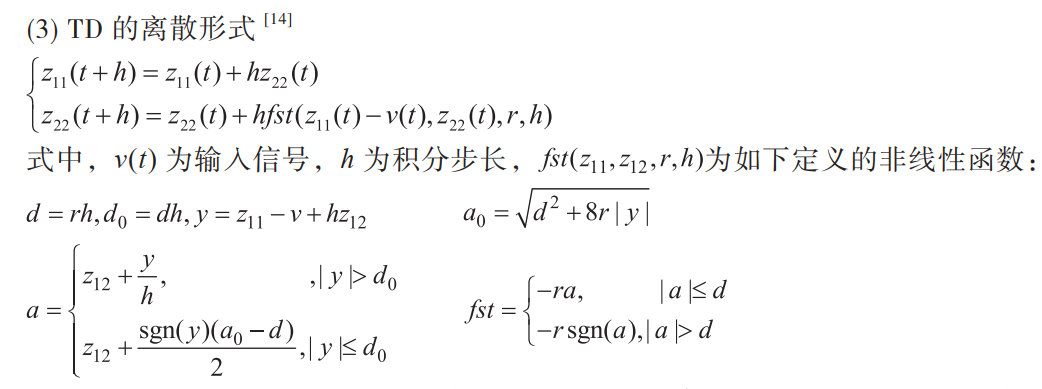
三:对TD数学表达式进行说明和讲解(从零讲起)
3.1 TD数学表达式的起源(起源是最速控制综合函数)
TD数学表达式本质上是对最速控制综合函数的一种变形

上图为最速控制综合函数的表达式
3.2 最速控制综合函数的推导(本章大量转载别人的博客,请见谅,会标明出处)
3.2.1 参考博客和论文
开源飞控ACFLY:ADRC离散系统最速控制综合函数的理解
离散系统最速控制综合函数(论文)
我对最速控制综合函数的理解很大一部分是参考了 开源飞控这篇博客里的说明,十分感谢大佬「听雨的声音233」的讲解。我在这里进行进一步的说明
3.2.2 最速控制综合函数的物理意义和数学建模
PS:在本章中以初中的小车运动为说明物理背景
这里改造的重点是红色方框。
r代表加速度。sgn函数括号里,x1代表当前位置,V(t)代表目标位置(下图有点错),x2代表当前速度。
本说明的所有变量声明表
| x1 | 位移 |
|---|---|
| x2 | 速度 |
| r | 加速度 |
| h | 积分步长(h在下文中出现) |
一,先看连续化的快速最优控制系统,主要是上图中最下面那条公式,这是什么意思?其实不难,你可以把等号左边的X1看作位置,X2看作速度,那么X1求导就是X2,(X1头上加一点就代表导数),那么X2的导数自然是加速度了,这是二阶积分系统。sgn函数我就不赘述了,r代表加速度。sgn函数括号里,x1代表当前位置,V(t)代表目标位置(下图有点错),x2代表当前速度。这个公式解决的是
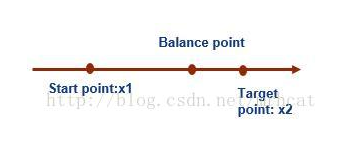
从一点到一点,先做匀加速运动再做匀减速运动并要求到达目标位置的速度为0,时间最短,问你什么时候应该加速什么时候应该减速。
x2|x2|/2r就是初中运动公式v2-v02=2ax指当前速度匀减速到0所需路长,x1-v(t)就是当前位置到目标位置的距离,只不过是负的,两者相加如果等于0,那么证明刚好到了平衡点,下一刻就应该减速了。大于小于0大家可以自己判断应该减速还是加速。
对于二阶离散系统的,我们仍然可以把x1(k)看作位置,把x(2)看作速度,h为积分步长,u(k)为控制量:加速度,u(k)<=r意思是控制量最大值为r,是人为调整的参数。离散和连续都是为了实现最速控制,所用时间最少**,且到达目标位置时速度为0,而且最终的目的坐标是0,即无超调,这是公式推导的基本要求,务必记住。
**

二.知道初始状态x1[0],x2[0],k步之后可推导出x1[k]和x2[k]的状态,化成矩阵形式如上图(可自己动手推导验证)。系统达到稳态是指达到目标位置,到达目标位置速度x2必须为0,x1即目标位置也设为0是为了方便计算系统初始值的表达式,假设初始位置x1[0]=1,目标位置是x1=3,现在变换一下,把目标位置的点设为=0,点还是那个点,只是坐标变化一下,那么初始位置也做相应变化x1[0]=-2;式4也很容易推导,最好自己动手推导一下。为什么要得到这个式子,这个式子是k步之内达到原点(即目标位置)所有初值和控制量的关系,初值是已知的,我们要反推出最佳控制量u[k]使得k步之内无超调最快达到目标。
说明补充部分:可以理解为
| 速度 | 时间X加速度 |
|---|---|
| X2 | hkr(积分步长*次数**加速度) |
| 位移 | △V*t的累加 |

三.可分3种情况反推出最优控制量u[k]。这是1步之内到达原点(即目标位置)的情况,把k=1代入式4便可得出式5,有两个点a-1,a+1相当于假设一步步长为1,当初始位置在1的时候可以一步走到原点(即目标位置),初始位置在-1的时候也可以一步走到原点(即目标位置),只不过方向相反而已。
Y轴表示速度 X轴表示相对于零点的位移量


四.这是第二种情况,k<=2内达到原点,与上面类似,不多说,都是为了反推出最优控制量。
说明补充部分: 关于这四个点可以这么理解
| 数学语言 | 物理语言 |
|---|---|
| [r,r] | [加速,加速] |
| [-r,r] | [减速,加速] |
| [r,-r] | [加速,减速] |
| [-r,-r] | [减速,减速] |
r为每个积分步长内的最大加速度

一个是恒加速或者恒减速。另一个是先加速后减速
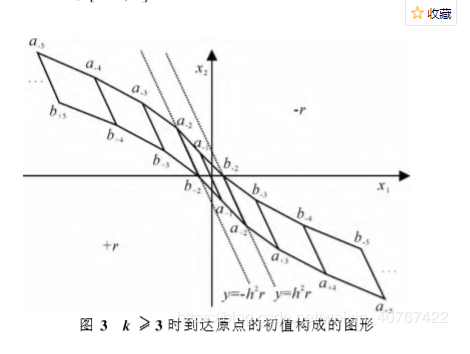

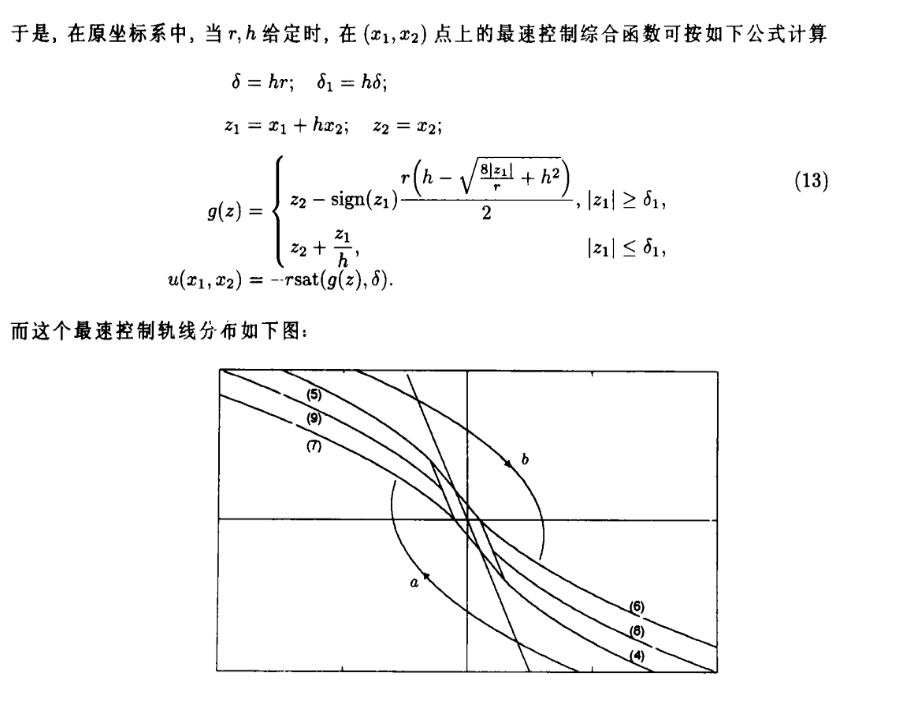
五.这是第3种情况,k>=3到达原点的情况。我刚开始看的时候就有一个疑问:给出最速轨迹线a后为什么还要给出轨迹b,后来我想明白了。
当我们的初始位置在最速轨迹线的时候当然最好,我们可以全速u[k]=r前进,足够靠近原点两步之内就能到达原点时,u[k]由情况2决定。
不然始终加速度最大为r,到达原点后会产生超调,就像一个人跑步,你到达终点前始终全速前进,到了终点由于速度不为0肯定还会向前移动,不符合文章开始说的无超调要求。
那当初始位置不在最速轨迹线上呢,那肯定得想方设法回到最速轨迹线上。假设初始位置在b-轨迹线的上方,要想回到最速轨迹线上,肯定得减速(这个不会看不出来吧),而且还是以最大加速度-r减速,不然怎么符合最速控制要求呢。
如果恰好减速到b-轨迹线上最好(请看上图文字b轨迹线代表什么),再以-r减速一步便可到达最速轨迹线Gbest线上。那如果减速到a线和b线之间呢,再以-r全力减速肯定到达不了Gbest线上,这就是为什么给出b轨迹线的原因。那当系统状态变量在a线和b线之间该如何求出最佳控制量?如下图:
重点说明部分部分,三种情况的分类说明。
六 :
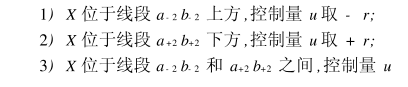
论文里面把工况分成了三种状态
| 情况一 | 在两步以内 |
|---|---|
| 情况二 | 三步及其以上的上方,控制量u=-r |
| 情况三 | 三步及其以上的下方,控制量u=+r |
| 重点 | 判断K的大小进行,三种情况的判断 |


七:通过式(16)用统一的一个方程将三种情况进行了统一三种工况。
式子(16)到式(26)的逻辑关系如下
| 式子代号 | 物理含义 |
|---|---|
| 18 | y=x1+hx2=当前位移+当前速度*积分步长=下一时刻的位移=0.5 X a X t^2 |
| 特别说明 | y的绝对值>h^2*r 代表此时小车在两步之外的范围 |
| 21 | 在经历了第k步的外力r作用后,小车可以在第(k-1)步以恒减加速度(-u)或者恒增加速度(+u)到达原点 |
| -22和23- | -式子(22)和式子(21)联立可以解得第k步里面外力u的大小:思路为在第k步的外力u的大小【此处需要强调外力u的大小最大值为r,有饱和值】- |
| 24 | 式子17的另一种表达形式 |
| 25 | 通过解方程x=1/2at^2(式子20)算的k的大小【注意一下,只需要判断k是否大于2,即在两步之外即可】通过式子(25)可以判断此时小车的在坐标图中的位置 |

最终式(27)为最速控制方程的数学表达式,注意:位移量为 x1-v(t) 即为当前位置到目标位置的距离,最终目的是位移量变为0.
h^2r:表示的是是否在两步的范围之内。
3.3 DT的离散形式 韩老先生把最速控制函数改造在自抗扰控制的DT中
原文链接:跟踪微分器的离散形式 韩京清
不BB直接上论文截图 注意一点x1(位移)和x2(速度)被z1和z2代替了
一边看论文一边看讲解。

3.3.1 k≥3的情况
到这里我估计只要你认真看了前面这里都都懂了,重点是下面

可能有的人面对式子(5)-(9)还能联想到,在a线上的恒减速运动。那么式子(10)-(12)有代表什么。
重点来了
式子(10)-(12)可以代表为
z2(速度)-sign(位移)X rkh= ±hr or 0 (这一步看不懂,去联想上个章节中k的算法)
速度减去加速度与时间=±hr 或者 0 零

接着通过对比sat函数,来使得外力u在[-r ,+r]之间合理波动。
3.3.2 k≤2 的情况
上面的都是3步及其以上的情况,最后是两步以内的简单情况。

3.3.3 最终结果
结果:两者综合得到最终值(离散表达式)
最后
以上就是无限酒窝最近收集整理的关于自抗扰控制入门之TD篇(纯小白入门向和TD数学表达式的推导)一:所用到的两篇参考论文和相关博客二:DT的基本数学表达式三:对TD数学表达式进行说明和讲解(从零讲起)的全部内容,更多相关自抗扰控制入门之TD篇(纯小白入门向和TD数学表达式内容请搜索靠谱客的其他文章。








发表评论 取消回复