OpenSSL密码库算法笔记——第5.4.12章 椭圆曲线的多倍点运算——固定点

        如果P点是固定的（比如基点）且存储空间允许的话，则可以事先进行预计算存储一些点以加快多倍点计算。有很多专门针对固定点计算的算法，比如固定点的窗口算法、固定点的梳形算法等，详情请参见[9,§5.2]。这里介绍的是B. Moller提出的wNAF分割法【Window NAF splitting】（ 详情参见[12]、[14]）。

        不太准确地说，wNAF算法是先把系数k分割成许多个宽为w的小块，然后在预计算阶段计算并存储点iP，i＝1, 3, 5, …, 2w－1－1。而wNAF分割法是在继承这一思想的基础上再把系数k进行一次新的划分，这一次划分的宽度v要比w大，比如取w＝4，v＝8。新一轮的划分完成后，需要预计算并存储更多的点：

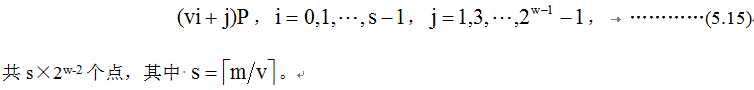
这样一来，在后面的计算阶段计算量从mD＋m/(w＋1)A减少到(v－1)D＋m/(w＋1)A。

wNAF分割法描述如下。

现在来稍微比较下wNAF算法和Moller提出的wNAF分割法。

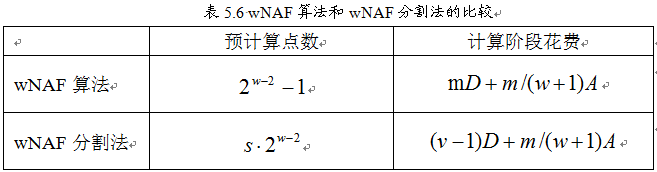
实现代码中基点的预计算函数就是采用这个思想，基点的预计算函数如下。

───────────────────────────────────────

int EC_GROUP_precompute_mult(EC_GROUP *group)

功能：    基点的预计算       

输入：    group

输出：    －

返回：    1【正常】 or 0【出错】

出处：    ec_mult.c

调用：    ▼    int ec_wNAF_precompute_mult(EC_GROUP *group)

备注：    调用的ec_wNAF_precompute_mult采用的是Moller的window NAF splitting算法。

───────────────────────────────────────

最后

以上就是幽默方盒为你收集整理的OpenSSL密码库算法笔记——第5.4.12章 椭圆曲线的多倍点运算——固定点的全部内容，希望文章能够帮你解决OpenSSL密码库算法笔记——第5.4.12章 椭圆曲线的多倍点运算——固定点所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。