1.相交链表

leetcode-160. 相交链表-简单
①哈希集合
使用哈希集合存储链表节点，首先遍历链表headA，并将链表headA 中的每个节点加入哈希集合中。然后遍历链表headB，对于遍历到的每个节点，判断该节点是否在哈希集合中。

var getIntersectionNode = function(headA, headB) {
    const visited=new Set();
    let temp=headA;
    while(temp!==null){
        visited.add(temp);
        temp=temp.next;
    }

    temp=headB;
    while(temp!==null){
        if(visited.has(temp)){
            return temp;
        }
        temp=temp.next;
    }
    return null;
};

时间复杂度：O(m+n)，其中m和n分别是链表headA 和headB的长度。需要遍历两个链表各一次。
空间复杂度：O(m)，其中 m是链表headA 的长度。需要使用哈希集合存储链表headA 中的全部节点。
②双指针
使用双指针的方法，可以将空间复杂度降至O(1)。

var getIntersectionNode = function(headA, headB) {
    
    // 当headA与headB都不为空时 才可能相交
    if(headA===null||headB===null) return null;

    // 双指针
    let p1=headA,p2=headB;
    while(p1!==p2){
        p1=p1===null?headB:p1.next;
        p2=p2===null?headA:p2.next;
    }
    return p1;
};

时间复杂度：O(m+n)，其中 m和 n分别是链表headA 和headB 的长度。两个指针同时遍历两个链表，每个指针遍历两个链表各一次。
空间复杂度：O(1)。
双指针的解法很巧妙啊，题解中证明该方法的正确性时考虑了两个链表相交和不相交的情况。（利用两个链表的长度来证明，考虑了两个链表长度一样和不一样的情况）

2.比特位计数

leetcode-338. 比特位计数-简单
题目： 给你一个整数 n ，对于 0 <= i <= n 中的每个 i ，计算其二进制表示中 1 的个数 ，返回一个长度为 n + 1 的数组 ans 作为答案。
部分编程语言有相应的内置函数用于计算给定的整数的二进制表示中的 1的数目，例如Java 的 Integer.bitCount，C++ 的__builtin_popcount，Go 的bits.OnesCount
以下方法均为不使用内置函数的解法????
①Brian Kernighan 算法
Brian Kernighan 算法的原理：对于任意整数x，令x=x & (x−1)，该运算将x的二进制表示的最后一个1变成0。直到x为0，该操作次数即为二进制中1的个数

var countBits = function(n) {
    const ans=new Array(n+1).fill(0);
    for(let i=0;i<=n;i++){
        ans[i]=countOnes(i);
    }
    return ans;
    
};
countOnes=(x)=>{
        let counts=0;
        while(x>0){
            x&=(x-1);
            counts++;
        }
        return counts;
    }

时间复杂度：O(nlogn)。需要对从0 到 n的每个整数使用计算「一比特数，即countOnes()」，对于每个整数计算「一比特数」的时间都不会超过O(logn)。
空间复杂度：O(1)，除了返回的数组以外，空间复杂度为常数。
②动态规划——最高有效位
③动态规划——最低有效位
④动态规划——最低设置位
⑤根据奇偶性
奇数：二进制表示中，奇数一定比前面那个偶数多一个 1
偶数：二进制表示中，偶数中 1 的个数一定和除以 2 之后的那个数一样多

var countBits = function(n) {
    const ans=new Array(n+1).fill(0);
    //根据奇偶性
    
    for(let i=1;i<=n;i++){
        if(i%2==0){
            ans[i]=ans[i/2];
        }else{
            ans[i]=ans[i-1]+1;
        }
    }
    return ans;
    
};

简洁版????

var countBits = function(n) {
    const ans=new Array(n+1).fill(0);
    //根据奇偶性
    // 简洁版
    for(let i=1;i<=n;i++){
        // 左移
        ans[i]=ans[i>>1]+(i&1);
    }
    return ans;
    
};

3.找到所有数组中消失的数字

leetcode-448. 找到所有数组中消失的数字-简单
①原地修改
用哈希表记录数组中出现的数字。由于数字范围均在[1,n]中，记录数字后我们再利用哈希表检查[1,n]中的每一个数是否出现，从而找到缺失的数字。
优化空间复杂度到O(1)，用nums充当哈希表

var findDisappearedNumbers = function(nums) {
    const len=nums.length;
    for(const num of nums){
        const x=(num-1)%len;
        nums[x]+=len;
    }
    const ans=[];
    for(const [i,num] of nums.entries()){
        if(num<=len){
            ans.push(i+1);
        }
    }
    return ans;
};

????不太理解
②
1.对nums排序并去重
2.循环比较长度为n的完整数组
3.当n中的某个值不存在于残缺的数组内时，push进一个空数组中返回

var findDisappearedNumbers = function(nums) {
    const len=nums.length;
    const sortNum=Array.from(new Set(nums.sort((a,b)=>a-b)));
    const ans=[];
    let n=0;
    for(let i=0;i<len;i++){
        n+=1;
        if(sortNum.indexOf(n)<0){
            ans.push(n);
        }
    }
    return ans;
};

时间复杂度好像略高...4956ms...解法①是92ms...

4.二叉树的直径

leetcode-543. 二叉树的直径-简单
题目： 给定一棵二叉树，你需要计算它的直径长度。一棵二叉树的直径长度是任意两个结点路径长度中的最大值。这条路径可能穿过也可能不穿过根结点。注：两结点之间的路径长度是以它们之间边的数目表示。

①深度优先搜索
深度优先搜索：大多使用递归函数。
递归函数三要素：
1.子问题与原问题做同样的事
2.需要求一个让递归结束的出口
3.递归表达式

let maxd=0;
var diameterOfBinaryTree = function(root) {
    depth(root);
    return maxd;
};
const depth=(root)=>{
    if(root==null) return 0;
    let left=depth(root.left);
    let right=depth(root.right);
    maxd=Math.max(left+right,maxd);
    return Math.max(left,right)+1;
}

执行代码时没问题，一提交就出错...

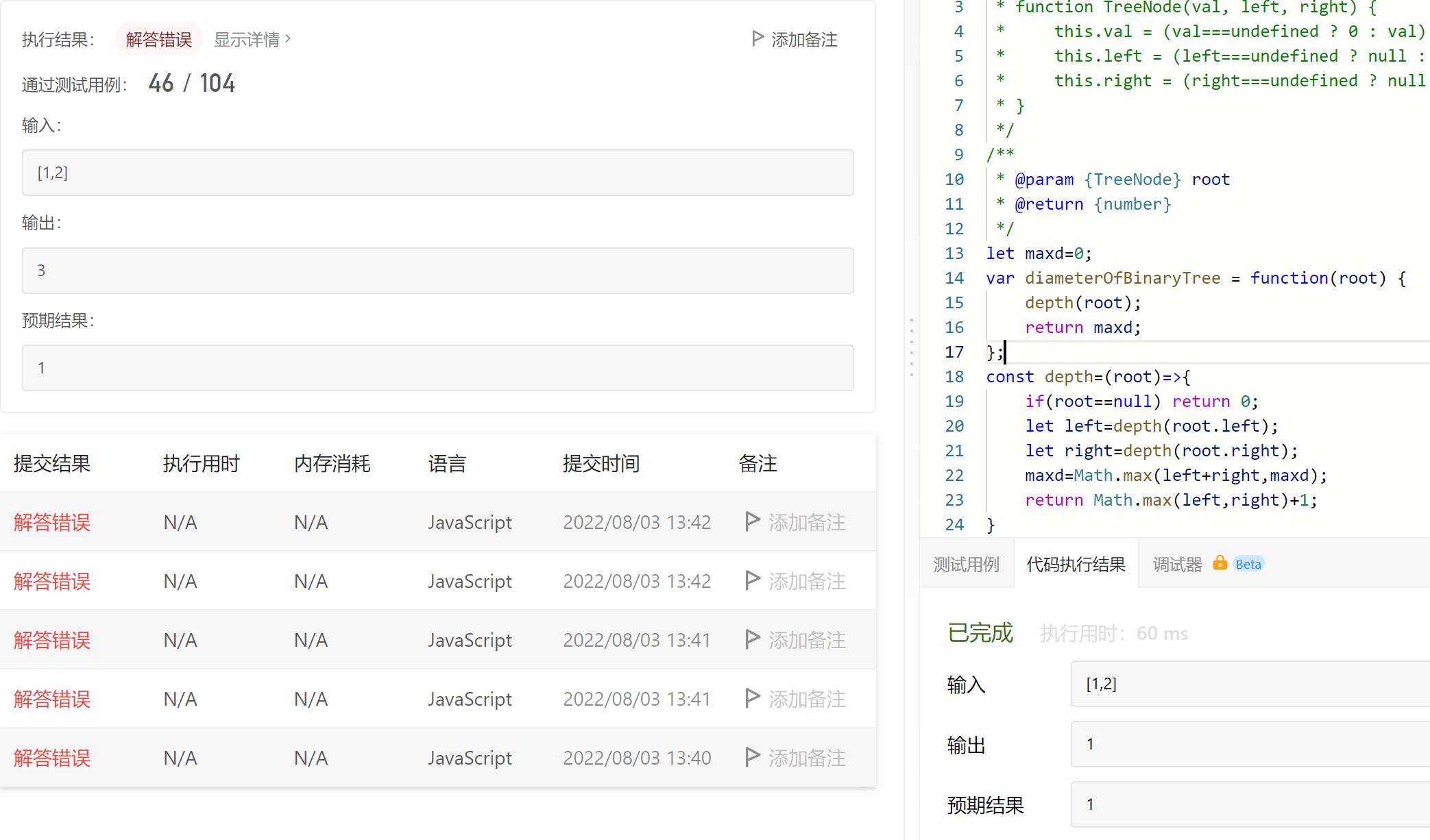
②计算二叉树某个非叶子节点的左右子树的最大高度和

var diameterOfBinaryTree = function(root) {
    // let height=0;
    function helper(node){
        if(node===null){
            return 0;
        }
        let left=helper(root.left),right=helper(root.right);
        height=Math.max(left+right,height);
        return Math.max(left,right)+1;
    }
     let height=0;
     helper(root);
     return height;
}

与答案一模一样的代码，报错...

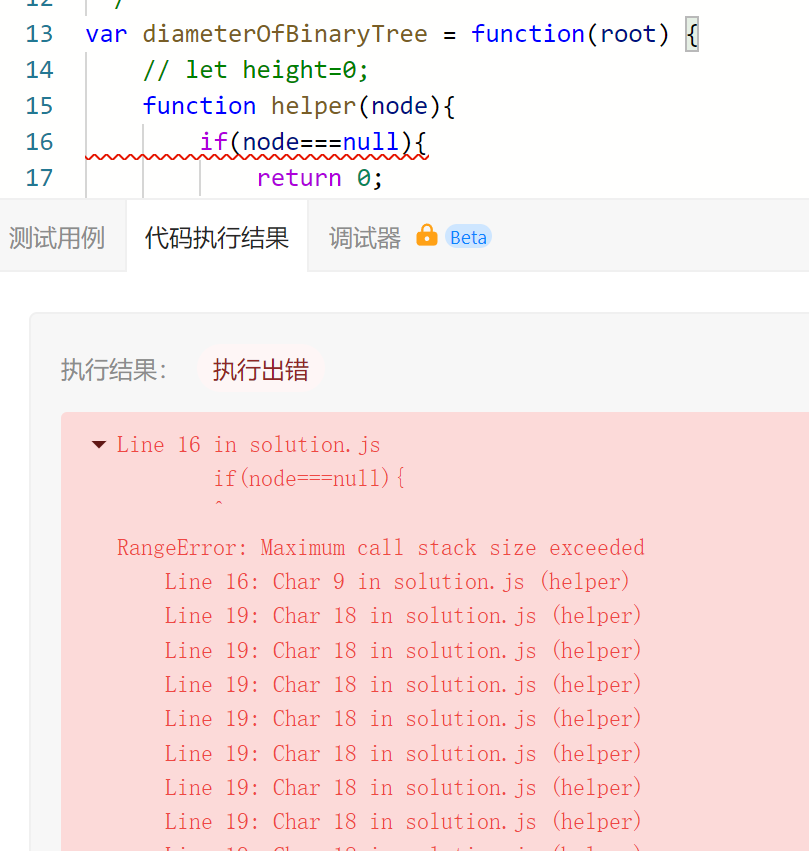
5.合并二叉树

leetcode-617. 合并二叉树-简单
①递归
嘿嘿，自己写出来了。简单题增加人的自信啊

var mergeTrees = function(root1, root2) {
    if(root1==null||root2==null) return root1==null?root2:root1;
    let root=new TreeNode();
    root.val=root1.val+root2.val;
    root.left=mergeTrees(root1.left,root2.left);
    root.right=mergeTrees(root1.right,root2.right);
    return root;
};

看官方解法，上述方法是深度优先搜索。
时间复杂度：O(min(m,n))，其中m和n分别是两个二叉树的节点个数。对两个二叉树同时进行深度优先搜索，只有当两个二叉树中的对应节点都不为空时才会对该节点进行显性合并操作，因此被访问到的节点数不会超过较小的二叉树的节点数。
空间复杂度：O(min(m,n))，其中m和n分别是两个二叉树的节点个数。空间复杂度取决于递归调用的层数，递归调用的层数不会超过较小的二叉树的最大高度，最坏情况下，二叉树的高度等于节点数。
②广度优先搜索

最后

以上就是怕孤独高跟鞋为你收集整理的leetcode每天5题-Day061.相交链表2.比特位计数3.找到所有数组中消失的数字4.二叉树的直径5.合并二叉树的全部内容，希望文章能够帮你解决leetcode每天5题-Day061.相交链表2.比特位计数3.找到所有数组中消失的数字4.二叉树的直径5.合并二叉树所遇到的程序开发问题。

如果觉得靠谱客网站的内容还不错，欢迎将靠谱客网站推荐给程序员好友。